Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T06:15:59.331Z Has data issue: false hasContentIssue false
  • English
  • Français

CENTRAL LIMIT THEOREM FOR PLANCK-SCALE MASS DISTRIBUTION OF TORAL LAPLACE EIGENFUNCTIONS

Part of: Miscellaneous applications of number theory Geometry of numbers Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  12 April 2019

Igor Wigman  and
Nadav Yesha
Igor Wigman
Affiliation:
Department of Mathematics, King’s College London, Strand, London WC2R 2LS, U.K. email igor.wigman@kcl.ac.uk
Nadav Yesha
Affiliation:
Department of Mathematics, King’s College London, Strand, London WC2R 2LS, U.K.
Get access

Abstract

We study the fine-scale 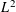$L^{2}$-mass distribution of toral Laplace eigenfunctions with respect to random position in two and three dimensions. In two dimensions, under certain flatness assumptions on the Fourier coefficients and generic restrictions on energy levels, both the asymptotic shape of the variance is determined and the limiting Gaussian law is established in the optimal Planck-scale regime. In three dimensions the asymptotic behaviour of the variance is analysed in a more restrictive scenario (“Bourgain’s eigenfunctions”). Other than the said precise results, lower and upper bounds are proved for the variance under more general flatness assumptions on the Fourier coefficients.

MSC classification

Primary: 11H06: Lattices and convex bodies 11Z05: Miscellaneous applications of number theory 35P20: Asymptotic distribution of eigenvalues and eigenfunctions
Type
Research Article
Information
Mathematika , Volume 65 , Issue 3 , 2019 , pp. 643 - 676
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: Department of Mathematics, University of Haifa, 3498838 Haifa, Israel email nyesha@univ.haifa.ac.il

References

Benatar, J. and Maffucci, R. W., Random waves on T3 : nodal area variance and lattice point correlations. Int. Math. Res. Not. IMRN 2017, doi:10.1093/imrn/rnx220.Google Scholar
Benatar, J., Marinucci, D. and Wigman, I., Planck-scale distribution of nodal length of arithmetic random waves. J. Anal. Math. (to appear).Google Scholar
Berry, M., Regular and irregular semiclassical wavefunctions. J. Phys. A 10(12) 1977, 2083–2091.Google Scholar
Berry, M., Semiclassical mechanics of regular and irregular motion. In Chaotic Behavior of Deterministic Systems (Les Houches, 1981), North-Holland (Amsterdam, 1983), 171–271.Google Scholar
Bombieri, E. and Bourgain, J., A problem on sums of two squares. Int. Math. Res. Not. IMRN 2015(11) 2015, 3343–3407.Google Scholar
Bourgain, J., On toral eigenfunctions and the random wave model. Israel J. Math. 201(2) 2014, 611–630.Google Scholar
Bourgain, J. and Rudnick, Z., On the geometry of the nodal lines of eigenfunctions of the two-dimensional torus. Ann. Henri Poincaré 12(6) 2011, 1027–1053.Google Scholar
Bourgain, J., Rudnick, Z. and Sarnak, P., Spatial statistics for lattice points on the sphere I: individual results. Bull. Iranian Math. Soc. 43(4) 2017, 361–386; special issue in honor of Freydoon Shahidi’s 70th birthday.Google Scholar
Colin de Verdière, Y., Ergodicité et fonctions propres du Laplacien. Comm. Math. Phys. 102 1985, 497–502.Google Scholar
de Courcy-Ireland, M., Small-scale equidistribution for random spherical harmonics. Preprint, 2017, arXiv:1711.01317.Google Scholar
Erdős, P. and Hall, R. R., On the angular distribution of Gaussian integers with fixed norm. Discrete Math. 200(1–3) 1999, 87–94.Google Scholar
Feller, W., An Introduction to Probability Theory and its Applications, Vol. 2, second edn., Wiley (New York, 1971).Google Scholar
Gradhsteyn, I. S. and Rizhik, I. M., Tables of Integrals, Series and Products, 6th edn., Academic Press (2000).Google Scholar
Granville, A. and Wigman, I., Planck-scale mass equidistribution of toral Laplace eigenfunctions. Comm. Math. Phys. 355(2) 2017, 767–802.Google Scholar
Han, X., Small scale quantum ergodicity in negatively curved manifolds. Nonlinearity 28(9) 2015, 3263–3288.Google Scholar
Han, X., Small scale equidistribution of random eigenbases. Comm. Math. Phys. 349(1) 2017, 425–440.Google Scholar
Han, X. and Tacy, M., Equidistribution of random waves on small balls. Preprint, 2016, arXiv:1611.05983.Google Scholar
Hezari, H. and Rivière, G., Quantitative equidistribution properties of toral eigenfunctions. J. Spectr. Theory 7(2) 2017, 471–485.Google Scholar
Hezari, H. and Rivière, G., L p norms, nodal sets, and quantum ergodicity. Adv. Math. 290 2016, 938–966.Google Scholar
Humphries, P., Equidistribution in shrinking sets and L 4 -norm bounds for automorphic forms. Math. Ann. 371(3–4) 2018, 1497–1543.Google Scholar
Krishnapur, M., Kurlberg, P. and Wigman, I., Nodal length fluctuations for arithmetic random waves. Ann. of Math. (2) 177(2) 2013, 699–737.Google Scholar
Kuipers, L. and Niederreiter, H., Uniform Distribution of Sequences, Wiley (New York, 1974).Google Scholar
Lester, S. and Rudnick, Z., Small scale equidistribution of eigenfunctions on the torus. Comm. Math. Phys. 350(1) 2017, 279–300.Google Scholar
Luo, W. Z. and Sarnak, P., Quantum ergodicity of eigenfunctions on PSL2(ℤ) \backslashℍ2 . Publ. Math. Inst. Hautes Études Sci. 81 1995, 207–237.Google Scholar
Sarnak, P., Variance sums on symmetric spaces. Private communication.Google Scholar
Sartori, A., Mass distribution for toral eigenfunctions via Bourgain’s de-randomisation. Preprint, 2018, arXiv:1812.00962.Google Scholar
Shnirelman, A., Ergodic properties of eigenfunctions. Uspekhi Mat. Nauk 180 1974, 181–182.Google Scholar
Young, M., The quantum unique ergodicity conjecture for thin sets. Adv. Math. 286 2016, 958–1016.Google Scholar
Zelditch, S., Uniform distribution of eigenfunctions on compact hyperbolic surfaces. Duke Math. J. 55 1987, 919–941.Google Scholar
Zygmund, A., On Fourier coefficients and transforms of functions of two variables. Studia Math. 50 1974, 189–201.Google Scholar