Article contents
Central sets in commutative semigroups and partition regularity of systems of linear equations
Published online by Cambridge University Press: 26 February 2010
Abstract
Given a commutative semigroup (S, +) with identity 0 and u × v matrices A and B with nonnegative integers as entries, we show that if C = A – B satisfies Rado's columns condition over ℤ, then any central set in S contains solutions to the system of equations 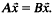 . In particular, the system of equations
. In particular, the system of equations 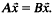 is then partition regular. Restricting our attention to the multiplicative semigroup of positive integers (so that coefficients become exponents) we show that the columns condition over ℤ is also necessary for the existence of solutions in any central set (while the distinct notion of the columns condition over Q is necessary and sufficient for partition regularity over ℕ\{1}).
is then partition regular. Restricting our attention to the multiplicative semigroup of positive integers (so that coefficients become exponents) we show that the columns condition over ℤ is also necessary for the existence of solutions in any central set (while the distinct notion of the columns condition over Q is necessary and sufficient for partition regularity over ℕ\{1}).
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1993
References
- 5
- Cited by

