Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T21:51:44.720Z Has data issue: false hasContentIssue false
  • English
  • Français

A CONVERSE THEOREM WITHOUT ROOT NUMBERS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  21 May 2019

Andrew R. Booker
Andrew R. Booker*
Affiliation:
Howard House, University of Bristol, Queen’s Avenue, Bristol BS8 1SN, U.K. email andrew.booker@bristol.ac.uk
Get access

Abstract

We answer a challenge posed in Booker [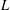$L$-functions as distributions. Math. Ann. 363(1–2) (2015), 423–454, §1.3] by proving a version of Weil’s converse theorem [Über die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen, Math. Ann. 168 (1967), 149–156] that assumes a functional equation for character twists but allows their root numbers to vary arbitrarily.

MSC classification

Primary: 11F11: Holomorphic modular forms of integral weight 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations
Type
Research Article
Information
Mathematika , Volume 65 , Issue 4 , 2019 , pp. 862 - 873
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was partially supported by EPSRC Grant EP/K034383/1.

References

Atkin, A. O. L. and Li, W. C. W., Twists of newforms and pseudo-eigenvalues of W-operators. Invent. Math. 48(3) 1978, 221–243; MR 508986.10.1007/BF01390245Google Scholar
Bettin, S., Bober, J. W., Booker, A. R., Conrey, B., Lee, M., Molteni, G., Oliver, T., Platt, D. J. and Steiner, R. S., A conjectural extension of Hecke’s converse theorem. Ramanujan J. 47(3) 2018, 659–684; MR 3874812.10.1007/s11139-017-9953-yGoogle Scholar
Booker, A. R., L-functions as distributions. Math. Ann. 363(1–2) 2015, 423–454; MR 3394385.10.1007/s00208-015-1178-zGoogle Scholar
Booker, A. R. and Krishnamurthy, M., A strengthening of the GL(2) converse theorem. Compos. Math. 147(3) 2011, 669–715; MR 2801397.10.1112/S0010437X10005087Google Scholar
Booker, A. R. and Krishnamurthy, M., Further refinements of the GL(2) converse theorem. Bull. Lond. Math. Soc. 45(5) 2013, 987–1003; MR 3104990.10.1112/blms/bdt031Google Scholar
Booker, A. R. and Krishnamurthy, M., Weil’s converse theorem with poles. Int. Math. Res. Not. IMRN 2014(19) 2014, 5328–5339; MR 3267373.10.1093/imrn/rnt127Google Scholar
Booker, A. R. and Krishnamurthy, M., A converse theorem for GL(n). Adv. Math. 296 2016, 154–180; MR 3490766.10.1016/j.aim.2016.03.041Google Scholar
Cogdell, J. W., Shahidi, F. and Tsai, T.-L., On stability of root numbers. In Automorphic Forms and Related Geometry: Assessing the Legacy of I. I. Piatetski–Shapiro (Contemporary Mathematics 614 ), American Mathematical Society (Providence, RI, 2014), 375–386; MR 3220935.10.1090/conm/614/12255Google Scholar
Conrey, J. B. and Farmer, D. W., An extension of Hecke’s converse theorem. Int. Math. Res. Not. IMRN 1995(9) 1995, 445–463; MR 1360623.10.1155/S1073792895000328Google Scholar
Deligne, P., Les constantes des équations fonctionnelles des fonctions L . In Modular Functions of One Variable II (Lecture Notes in Mathematics 349 ) (eds Deligne, P. and Kuyk, W.), Springer (Berlin, 1973), 501–597; MR 0349635.10.1007/978-3-540-37855-6_7Google Scholar
Diaconu, A., Perelli, A. and Zaharescu, A., A note on GL2 converse theorems. C. R. Math. Acad. Sci. Paris 334(8) 2002, 621–624; MR 1903358 (2003f:11066).10.1016/S1631-073X(02)02277-XGoogle Scholar
Jacquet, H. and Langlands, R. P., Automorphic forms on GL(2) (Lecture Notes in Mathematics 114 ), Springer (Berlin, 1970); MR 0401654 (53 #5481).10.1007/BFb0058988Google Scholar
Kaczorowski, J., Molteni, G. and Perelli, A., Linear independence in the Selberg class. C. R. Math. Acad. Sci. Soc. R. Can. 21(1) 1999, 28–32; MR 1669479 (2000h:11094).Google Scholar
Langlands, R. P., Author’s comments on “Correspondence leading to the book written with Jacquet”, http://publications.ias.edu/rpl/paper/53.Google Scholar
Langlands, R. P., Author’s comments on “Problems in the theory of automorphic forms”, http://publications.ias.edu/rpl/paper/47.Google Scholar
Langlands, R. P., On the functional equation of the Artin $L$ -functions, http://publications.ias.edu/sites/default/files/a-ps.pdf.Google Scholar
Li, W. C. W., Newforms and functional equations. Math. Ann. 212 1975, 285–315; MR 0369263.10.1007/BF01344466Google Scholar
Miyake, T., Modular forms (Springer Monographs in Mathematics), English edn., Springer (Berlin, 2006), translated from the 1976 Japanese original by Yoshitaka Maeda; MR 2194815 (2006g:11084).Google Scholar
Steiner, R. S., Near counterexamples to Weil’s converse theorem. Preprint, 2017, arXiv:1606.06923.Google Scholar
Weil, A., Über die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen. Math. Ann. 168 1967, 149–156; MR 0207658 (34 #7473).10.1007/BF01361551Google Scholar