No CrossRef data available.
Article contents
Convex semi-lattices of continuous functions
Published online by Cambridge University Press: 26 February 2010
Extract
The purpose of this note is to settlo a question that was left incompletely solved in the author's paper [1].
Let E be a compact Hausdorff space, and C(E) the class of all continuous real-valued functions on E. A subset F of C(E) is called an upper semi-lattice (or, more briefly, is said to admit ں) if ƒ ں g ε F whenever ƒ, g ε F. A subset F of C(E) is said to be upper semi-equicontinuous (u.s.e.c.) if for every ε > 0 and s ε E there exists a neighbourhood U of s such that
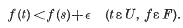
We say that F is locally u.s.e.c. if every uniformly bounded subset of F is u.s.e.c.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1960
References
1.Bonsall, F. F., “Semi-algebras of continuous functions”, Proc. London Math. Soc. (3), 10 (1960), 122–140.Google Scholar
2.Choquet, G. and Deny, J., “Ensembles semi-réticulés et ensembles réticulés de fonctions continues”, Journal de Math. Pures et Appliquées, 36 (1957), 179–189.Google Scholar

