Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-28T07:18:45.467Z Has data issue: false hasContentIssue false
  • English
  • Français

The delay differential equation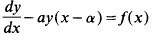

Part of: Functional-differential and differential-difference equations

Published online by Cambridge University Press:  26 February 2010

LL. G. Chambers
LL. G. Chambers
Affiliation:
Department of Applied Mathematics and Computation, University College of North Wales, Bangor, Gwynedd, LL57 2UW
Get access

Extract

The usual method of dealing with delay differential equations such as

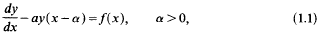
is the method of steps [1, 2]. In this, y(x) is assumed to be known for − α < x < 0, thereby defining 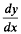over 0 < x < α. As a result of integration, the value of y is now known over 0 < x < α, and the integration proceeds thereon by a succession of steps.

MSC classification

Secondary: 34K10: Boundary value problems

Information

Type
Research Article
Information
Mathematika , Volume 33 , Issue 1 , June 1986 , pp. 80 - 86
Copyright
Copyright © University College London 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1.Driver, R. D.. Ordinary and Delay Differential Equations (Springer-Verlag, New York, 1977) 226.CrossRefGoogle Scholar
2.Hale, Jack. Theory of Functional Differential Equations (Springer-Verlag, New York, 1977) 15.CrossRefGoogle Scholar
3.Driver, R. D.. Loc. cit, 321.Google Scholar
4.Hale, Jack. Loc. cit, 17.Google Scholar
5.Conte, S. D. and de Boor, Carl. Elementary Numerical Analysis (McGraw-Hill-Kogakusha, Tokyo, 1972) 143.Google Scholar