Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T21:53:44.287Z Has data issue: false hasContentIssue false
  • English
  • Français

DENOMINATORS OF BERNOULLI POLYNOMIALS

Part of: Sequences and sets Multiplicative number theory

Published online by Cambridge University Press:  16 April 2018

Olivier Bordellès ,
Florian Luca ,
Pieter Moree  and
Igor E. Shparlinski
Olivier Bordellès
Affiliation:
2 Allée de la combe, 43000 Aiguilhe, France email borde43@wanadoo.fr
Florian Luca
Affiliation:
School of Mathematics, University of the Witwatersrand, Private Bag X3, Wits 2050, South Africa Max Planck Institute for Mathematics, Vivatsgasse 7, 53111 Bonn, Germany Department of Mathematics, Faculty of Sciences, University of Ostrava, 30 Dubna 22, 701 03 Ostrava 1, Czech Republic email florian.luca@wits.ac.za
Pieter Moree
Affiliation:
Max Planck Institute for Mathematics, Vivatsgasse 7, 53111 Bonn, Germany email moree@mpim-bonn.mpg.de
Igor E. Shparlinski
Affiliation:
Department of Pure Mathematics, University of New South Wales, 2052 NSW, Australia email igor.shparlinski@unsw.edu.au
Get access

Abstract

For a positive integer $n$ let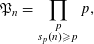

$$\begin{eqnarray}\mathfrak{P}_{n}=\mathop{\prod }_{\substack{ p \\ s_{p}(n)\geqslant p}}p,\end{eqnarray}$$
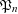where $p$ runs over primes and $s_{p}(n)$ is the sum of the base $p$ digits of $n$. For all $n$ we prove that $\mathfrak{P}_{n}$ is divisible by all “small” primes with at most one exception. We also show that 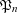$\mathfrak{P}_{n}$ is large and has many prime factors exceeding 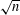$\sqrt{n}$, with the largest one exceeding 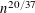$n^{20/37}$. We establish Kellner’s conjecture that the number of prime factors exceeding 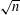$\sqrt{n}$ grows asymptotically as 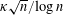$\unicode[STIX]{x1D705}\sqrt{n}/\text{log}\,n$ for some constant $\unicode[STIX]{x1D705}$ with 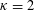$\unicode[STIX]{x1D705}=2$. 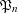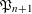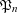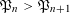Further, we compare the sizes of $\mathfrak{P}_{n}$ and $\mathfrak{P}_{n+1}$, leading to the somewhat surprising conclusion that although $\mathfrak{P}_{n}$ tends to infinity with $n$, the inequality $\mathfrak{P}_{n}>\mathfrak{P}_{n+1}$ is more frequent than its reverse.

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Secondary: 11B68: Bernoulli and Euler numbers and polynomials
Type
Research Article
Information
Mathematika , Volume 64 , Issue 2 , 2018 , pp. 519 - 541
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards, Wiley-Interscience (New York, 1972), 10th printing, with corrections.Google Scholar
Baker, R. and Harman, G., The sequence x/n and its subsequences. Rocky Mountain J. Math. 26 1996, 795–814.Google Scholar
Baker, R. C. and Harman, G., Small remainder of a vector to suitable modulus. Math. Zeit. 221 1996, 59–71.Google Scholar
Bordellès, O., Arithmetic Tales (Universitext), Springer (London, 2012).CrossRefGoogle Scholar
Bugeaud, Y., Mignotte, M. and Siksek, S., Classical and modular approaches to exponential Diophantine equations I. Fibonacci and Lucas perfect powers. Ann. of Math. (2) 163 2006, 969–1018.Google Scholar
Erdős, P. and Wagstaff, S., The fractional parts of the Bernoulli numbers. Illinois J. Math. 24 1980, 104–112.Google Scholar
Ford, K., Integers divisible by a large shifted prime. Acta Arith. 178 2017, 163–180.Google Scholar
Granville, A. and Ramaré, O., Explicit bounds on exponential sums and the scarcity of squarefree binomial coefficients. Mathematika 43 1996, 73–107.Google Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, Oxford University Press (Oxford, 1979).Google Scholar
Ivić, A., The Riemann Zeta-Function. Theory and Applications, Dover (Mineola, NY, 2003).Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society (Providence, RI, 2004).Google Scholar
Kellner, B. C., On a product of certain primes. J. Number Theory 179 2017, 126–141.Google Scholar
Kellner, B. C. and Sondow, J., Power-sum denominators. Amer. Math. Monthly 124 2017, 695–709.Google Scholar
Kellner, B. C. and Sondow, J., The denominators of power sums of arithmetic progressions. Preprint, 2017, arXiv:1705.05331.Google Scholar
Luca, F., Pizarro-Madariaga, A. and Pomerance, C., On the counting function of irregular primes. Indag. Math. (N.S.) 26 2015, 147–161.Google Scholar
Matveev, E. M., An explicit lower bound for a homogeneous rational linear form in the logarithms of algebraic numbers, II. Izv. Ross. Akad. Nauk Ser. Mat. 64 2000, 125–180; Engl. transl. Izv. Math. 64 (2000), 1217–1269.Google Scholar
McNew, N., Pollack, P. and Pomerance, C., Numbers divisible by a large shifted primes and torsion subgroups of CM ellipitic curves. Int. Math. Res. Not. IMRN 2017 2017, 5525–5553.Google Scholar
Senge, H. G. and Straus, E. G., PV-numbers and sets of multiplicity. Period. Math. Hungar. 3 1973, 93–100.Google Scholar
Stewart, C. L., On the representation of an integer in two different bases. J. Reine Angew. Math. 319 1980, 63–72.Google Scholar
Vaaler, J. D., Some extremal functions in Fourier analysis. Bull. Amer. Math. Soc. (N.S.) 12 1985, 183–215.CrossRefGoogle Scholar