Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-29T04:35:57.056Z Has data issue: false hasContentIssue false
  • English
  • Français

DIOPHANTINE APPROXIMATION ON MANIFOLDS AND LOWER BOUNDS FOR HAUSDORFF DIMENSION

Published online by Cambridge University Press:  29 November 2017

Victor Beresnevich ,
Lawrence Lee ,
Robert C. Vaughan  and
Sanju Velani
Victor Beresnevich
Affiliation:
University of York, Heslington, York YO10 5DD, U.K. email victor.beresnevich@york.ac.uk
Lawrence Lee
Affiliation:
University of York, Heslington, York YO10 5DD, U.K. email ldl503@york.ac.uk
Robert C. Vaughan
Affiliation:
Department of Mathematics, McAllister Building, Pennsylvania State University, University Park, PA 16802-6401, U.S.A. email rcv4@psu.edu
Sanju Velani
Affiliation:
University of York, Heslington, York YO10 5DD, U.K. email sanju.velani@york.ac.uk
Get access

Abstract

Given 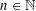$n\in \mathbb{N}$ and 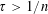$\unicode[STIX]{x1D70F}>1/n$, let 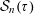${\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})$ denote the classical set of $\unicode[STIX]{x1D70F}$-approximable points in 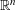$\mathbb{R}^{n}$, which consists of 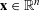$\mathbf{x}\in \mathbb{R}^{n}$ that lie within distance 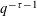$q^{-\unicode[STIX]{x1D70F}-1}$ from the lattice 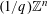$(1/q)\mathbb{Z}^{n}$ for infinitely many 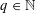$q\in \mathbb{N}$. In pioneering work, Kleinbock and Margulis showed that for any non-degenerate submanifold 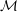${\mathcal{M}}$ of 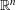$\mathbb{R}^{n}$ and any 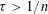$\unicode[STIX]{x1D70F}>1/n$ almost all points on 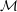${\mathcal{M}}$ are not $\unicode[STIX]{x1D70F}$-approximable. Numerous subsequent papers have been geared towards strengthening this result through investigating the Hausdorff measure and dimension of the associated null set 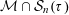${\mathcal{M}}\cap {\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})$. In this paper we suggest a new approach based on the Mass Transference Principle of Beresnevich and Velani [A mass transference principle and the Duffin–Schaeffer conjecture for Hausdorff measures. Ann. of Math. (2) 164(3) (2006), 971–992], which enables us to find a sharp lower bound for $\dim {\mathcal{M}}\cap {\mathcal{S}}_{n}(\unicode[STIX]{x1D70F})$ for any 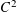$C^{2}$ submanifold 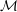${\mathcal{M}}$ of $\mathbb{R}^{n}$ and any $\unicode[STIX]{x1D70F}$ satisfying 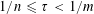$1/n\leqslant \unicode[STIX]{x1D70F}<1/m$. Here 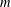$m$ is the codimension of 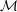${\mathcal{M}}$. We also show that the condition on $\unicode[STIX]{x1D70F}$ is best possible and extend the result to general approximating functions.

Type
Research Article
Information
Mathematika , Volume 63 , Issue 3 , 2017 , pp. 762 - 779
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beresnevich, V., Rational points near manifolds and metric Diophantine approximation. Ann. of Math. (2) 175(1) 2012, 187–235.CrossRefGoogle Scholar
Beresnevich, V., Bernik, V., Dodson, M. and Velani, S., Classical metric diophantine approximation revisited. In Analytic Number Theory. Essays in Honour of Klaus Roth on the Occasion of his 80th Birthday (eds William, W. C., Gowers, T., Halberstam, H., Schmidt, W. and Vaughan, B.), Cambridge University Press (Cambridge, 2009), 38–61.Google Scholar
Beresnevich, V., Dickinson, D. and Velani, S., Measure theoretic laws for limsup sets. Mem. Amer. Math. Soc. 179(846) 2006, 1–91.Google Scholar
Beresnevich, V., Dickinson, D. and Velani, S., Diophantine approximation on planar curves and the distribution of rational points. With an Appendix II by R. C. Vaughan. Ann. of Math. (2) 166(2) 2007, 367–426.CrossRefGoogle Scholar
Beresnevich, V., Ramírez, F. and Velani, S., Metric Diophantine approximation: aspects of recent work. In Dynamics and Analytic Number Theory (LMS Lecture Note Series 437 ) (eds Badziahin, D., Gorodnik, A. and Peyerimhoff, N.), Cambridge University Press (Cambridge, 2016), 1–95.Google Scholar
Beresnevich, V., Vaughan, R. and Velani, S., Inhomogeneous Diophantine approximation on planar curves. Math. Ann. 349(4) 2011, 929–942.CrossRefGoogle Scholar
Beresnevich, V., Vaughan, R., Velani, S. and Zorin, E., Diophantine approximation on manifolds and the distribution of rational points: contributions to the convergence theory. Int. Math. Res. Not. IMRN published online, 2016.Google Scholar
Beresnevich, V., Vaughan, R., Velani, S. and Zorin, E., Diophantine approximation on manifolds and the distribution of rational points: contributions to the divergence theory. In preparation.Google Scholar
Beresnevich, V. and Velani, S., A mass transference principle and the Duffin–Schaeffer conjecture for Hausdorff measures. Ann. of Math. (2) 164(3) 2006, 971–992.CrossRefGoogle Scholar
Beresnevich, V. and Velani, S., A note on simultaneous Diophantine approximation on planar curves. Math. Ann. 337(4) 2007, 769–796.CrossRefGoogle Scholar
Beresnevich, V. and Velani, S., A note on zero-one laws in metrical Diophantine approximation. Acta Arith. 133(4) 2008, 363–374.CrossRefGoogle Scholar
Beresnevich, V. and Velani, S., A note on three problems in metric Diophantine approximation. In Recent Trends in Ergodic Theory and Dynamical Systems (Contemporary Mathematics 631 ), Amer. Math. Soc. (Providence, RI, 2015), 211–229.Google Scholar
Beresnevich, V. and Zorin, E., Explicit bounds for rational points near planar curves and metric Diophantine approximation. Adv. Math. 225(6) 2010, 3064–3087.CrossRefGoogle Scholar
Bernik, V. and Dodson, M., Metric Diophantine Approximation on Manifolds (Cambridge Tracts in Mathematics 137 ), Cambridge University Press (Cambridge, 1999).CrossRefGoogle Scholar
Besicovitch, A., Sets of fractional dimensions IV: on rational approximation to real numbers. J. Lond. Math. Soc. 9 1934, 126–131.CrossRefGoogle Scholar
Dickinson, H. and Dodson, M., Extremal manifolds and Hausdorff dimension. Duke Math. J. 101(2) 2000, 271–281.CrossRefGoogle Scholar
Dickinson, H. and Velani, S., Hausdorff measure and linear forms. J. Reine Angew. Math. 490 1997, 1–36.Google Scholar
Falconer, K., The Geometry of Fractal Sets (Cambridge Tracts in Mathematics 85 ), Cambridge University Press (Cambridge, 1985).CrossRefGoogle Scholar
Huang, J.-J., Rational points near planar curves and Diophantine approximation. Adv. Math. 274 2015, 490–515.CrossRefGoogle Scholar
Jarník, I., Sur les approximations Diophantiennes des nombres p-adiques. revista Ci Lima 47 489–505.Google Scholar
Khintchine, A., Einige Sätze über Kettenbrüche, mit Anwendungen auf die Theorie der Diophantischen Approximationen. Math. Ann. 92 1924, 115–125.CrossRefGoogle Scholar
Kleinbock, D., Extremal subspaces and their submanifolds. Geom. Funct. Anal. 13(2) 2003, 437–466.CrossRefGoogle Scholar
Kleinbock, D. and Margulis, G., Flows on homogeneous spaces and Diophantine approximation on manifolds. Ann. of Math. (2) 148(1) 1998, 339–360.CrossRefGoogle Scholar
Kleinbock, D., Lindenstrauss, E. and Weiss, B., On fractal measures and Diophantine approximation. Selecta Math. (N.S.) 10 2004, 479–523.CrossRefGoogle Scholar
Pollington, A. and Velani, S., Metric Diophantine approximation and ‘absolutely friendly’ measures. Selecta Math. (N.S.) 11 2005, 297–307.CrossRefGoogle Scholar
Ramírez, F., Khintchine types of translated coordinate hyperplanes. Acta Arith. 170(3) 2015, 243–273.CrossRefGoogle Scholar
Ramŕez, F., Simmons, D. and Süess, F., Rational approximation of affine coordinate subspaces of Euclidean space. Acta Arith. 177 2017, 91–100.CrossRefGoogle Scholar
Schmidt, W., Diophantine Approximation (Lecture Notes in Mathematics 785 ), Springer (Berlin, 1980).Google Scholar
Simmons, D., Some manifolds of Khintchin type for convergence. Preprint, 2016, arXiv:1602.01727.Google Scholar
Vaughan, R. and Velani, S., Diophantine approximation on planar curves: the convergence theory. Invent. Math. 166(1) 2006, 103–124.CrossRefGoogle Scholar