Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T07:26:20.506Z Has data issue: false hasContentIssue false
  • English
  • Français

DIRECTED SIMPLICES IN HIGHER ORDER TOURNAMENTS

Part of: Graph theory

Published online by Cambridge University Press:  10 December 2009

Imre Leader  and
Ta Sheng Tan
Imre Leader*
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WB, U.K. (email: I.Leader@dpmms.cam.ac.uk)
Ta Sheng Tan
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WB, U.K. (email: T.S.Tan@dpmms.cam.ac.uk)
*
✉For correspondence; e-mail: I.Leader@dpmms.cam.ac.uk
Get access

Abstract

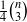It is well known that a tournament (complete oriented graph) on n vertices has at most directed triangles, and that the constant is best possible. Motivated by some geometric considerations, our aim in this paper is to consider some “higher order” versions of this statement. For example, if we give each 3-set from an n-set a cyclic ordering, then what is the greatest number of “directed 4-sets” we can have? We give an asymptotically best possible answer to this question, and give bounds in the general case when we orient each d-set from an n-set.

MSC classification

Secondary: 05C65: Hypergraphs 05C20: Directed graphs (digraphs), tournaments
Type
Research Article
Information
Mathematika , Volume 56 , Issue 1 , January 2010 , pp. 173 - 181
Copyright
Copyright © University College London 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bárány, I., A generalization of Carathéodory’s theorem. Discrete Math. 40 (1982), 141–152.CrossRefGoogle Scholar
[2]Boros, E. and Füredi, Z., Su un teorema di Kárteszi nella geometria combinatoria. Archimede 2 (1977), 71–76.Google Scholar
[3]Boros, E. and Füredi, Z., The number of triangles covering the center of an n-set. Geom. Dedicata 17 (1984), 69–77.CrossRefGoogle Scholar
[4]Bukh, B., A point in many triangles. Electron. J. Combin. 13(1) (2006), N10.CrossRefGoogle Scholar
[5]Bukh, B., Matoušek, J. and Nivasch, G., Stabbing simplices by points and flats, Discrete Comput. Geom., (to appear).Google Scholar
[6]Kárteszi, F., Extremalaufgaben über endliche Punktsysteme. Publ. Math. Debrecen 4 (1955), 16–27.CrossRefGoogle Scholar
[7]McMullen, P. and Shephard, G. C., Convex Polytopes and the Upper Bound Conjecture, Cambridge University Press (Cambridge, 1971).CrossRefGoogle Scholar
[8]Moon, J. W., Topics on Tournaments, Holt, Rinehart and Winston (New York, 1968).Google Scholar
[9]Wagner, U., On k-sets and applicatons. PhD Thesis, ETH Zürich, 2003.Google Scholar