Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-13T06:29:11.865Z Has data issue: false hasContentIssue false
  • English
  • Français

Extreme points of convex sets without completeness of the Scalar field

Published online by Cambridge University Press:  26 February 2010

Victor Klee
Victor Klee
Affiliation:
University of Washington, Seattle, Washington, U.S.A.
Get access

Extract

Throughout this paper, E will denote a finite-dimensional vector space over an ordered field 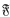. The real number field will be denoted by ℜ and its rational subfield by 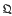. Many of the basic notions in the theory of convexity (convex set, extreme point, hyperplane, etc.) can be defined in the general case just as they are when 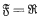, but their behaviour may be different from that in the real case. By way of example, we consider the following theorem (due essentially to Minkowski), which is of fundamental importance both for geometric investigations and for the applications of convexity in analysis:

(1) Suppose 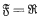. If K is a convex subset of E which is linearly closed and linearly bounded, then. K = con ex K; that is, K is the convex hull of its set of extreme points.

Type
Research Article
Information
Mathematika , Volume 11 , Issue 1 , June 1964 , pp. 59 - 63
Copyright
Copyright © University College London 1964

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Klee, V., “Extremal structure of convex sets”, Arch. Math., 8 (1957), 234–240.CrossRefGoogle Scholar
2.Klee, V., “Some characterizations of convex polyhedra”, Acta Math., 102 (1959), 79–107.CrossRefGoogle Scholar
3.Klee, V., “On a theorem of Dubins”, J. Math. Anal. Appl., 7 (1963), 425–427.CrossRefGoogle Scholar
4.Weyl, H., “Elementare Theorie der konvexen Polyeder”, Comm. Math. Helvetici, 7 (1935), 290–306.CrossRefGoogle Scholar
(English translation by Kuhn, H. W. in Annals of Math. Studies (Princeton), 24 (1950), 3–18.)Google Scholar