Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T23:04:39.354Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITE FLAT SPACES

Part of: Metric geometry

Published online by Cambridge University Press:  14 August 2019

Vladimir Zolotov
Vladimir Zolotov*
Affiliation:
Steklov Institute of Mathematics, Russian Academy of Sciences, 27 Fontanka, 191023 St. Petersburg, Russia University of Cologne, Albertus-Magnus-Platz, 50923 Köln, Germany Mathematics and Mechanics Faculty, St. Petersburg State University, Universitetsky pr., 28, Stary Peterhof, 198504, Russia email paranuel@mail.ru
Get access

Abstract

We say that a finite metric space 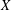$X$ can be embedded almost isometrically into a class of metric spaces 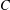$C$ if for every 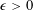$\unicode[STIX]{x1D716}>0$ there exists an embedding of 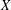$X$ into one of the elements of 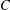$C$ with the bi-Lipschitz distortion less than 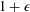$1+\unicode[STIX]{x1D716}$. We show that almost isometric embeddability conditions are equal for the following classes of spaces.

  1. (a) Quotients of Euclidean spaces by isometric actions of finite groups.

  2. (b) 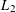$L_{2}$-Wasserstein spaces over Euclidean spaces.

  3. (c) Compact flat manifolds.

  4. (d) Compact flat orbifolds.

  5. (e) Quotients of connected compact bi-invariant Lie groups by isometric actions of compact Lie groups. (This one is the most surprising.)

We call spaces which satisfy these conditions finite flat spaces. Since Markov-type constants depend only on finite subsets, we can conclude that connected compact bi-invariant Lie groups and their quotients have Markov type 2 with constant 1.

MSC classification

Primary: 51F99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 65 , Issue 4 , 2019 , pp. 1010 - 1017
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexander, S., Kapovitch, V. and Petrunin, A., Alexandrov meets Kirszbraun. In Proc. 17th Gokova Geometry–Topology Conf., 2010, International Press (Somerville, MA, 2010), 88–109.Google Scholar
Andoni, A., Naor, A. and Neiman, O., Snowflake universality of Wasserstein spaces. Ann. Sci. Éc. Norm. Supér. (4) 51(3) 2018, 657–700.10.24033/asens.2363Google Scholar
Ball, K., Markov chains, Riesz transforms and Lipschitz maps. Geom. Funct. Anal. 2(2) 1992, 137–172.10.1007/BF01896971Google Scholar
Bartal, Y., Linial, N., Mendel, M. and Naor, A., On metric Ramsey-type phenomena. In Proc. Thirty-fifth Annu. ACM Sympos. Theory of Computing, STOC ’03, ACM (New York, NY, 2003), 463–472.10.1145/780542.780610Google Scholar
Bettiol, R. G., Derdzinski, A. and Piccione, P., Teichmüller theory and collapse of flat manifolds. Ann. Mat. Pura Appl. (4) 197(4) 2018, 1247–1268.10.1007/s10231-017-0723-7Google Scholar
Bieberbach, L., Über die Bewegungsgruppen der Euklidischen Räume. Math. Ann. 70(3) 1911, 297–336.10.1007/BF01564500Google Scholar
Bieberbach, L., Über die Bewegungsgruppen der Euklidischen Räume. (Zweite Abhandlung.) Die Gruppen mit einem endlichen Fundamentalbereich. Math. Ann. 72(3) 1912, 400–412.10.1007/BF01456724Google Scholar
Deza, M. M. and Laurent, M., Geometry of Cuts and Metrics, Vol. 15, Springer (2009).Google Scholar
Galaz-Garcia, F., Kell, M., Mondino, A. and Sosa, G., On quotients of spaces with Ricci curvature bounded below. J. Funct. Anal. 275(6) 2018, 1368–1446.10.1016/j.jfa.2018.06.002Google Scholar
Lebedeva, N., Petrunin, A. and Zolotov, V., Bipolar comparison. Geom. Funct. Anal. 29(1) 2019, 258–282.10.1007/s00039-019-00481-9Google Scholar
Linial, N., Magen, A. and Naor, A., Girth and Euclidean distortion. Geom. Funct. Anal. 12(2) 2002, 380–394.10.1007/s00039-002-8251-yGoogle Scholar
Naor, A., An introduction to the Ribe program. Jpn. J. Math. 7(2) 2012, 167–233.10.1007/s11537-012-1222-7Google Scholar
Naor, A., Peres, Y., Schramm, O. and Sheffield, S., Markov chains in smooth Banach spaces and Gromov-hyperbolic metric spaces. Duke Math. J. 134(1) 2006, 165–197.10.1215/S0012-7094-06-13415-4Google Scholar
Nash, J., C 1 isometric imbeddings. Ann. of Math. (2) 60(3) 1954, 383–396.10.2307/1969840Google Scholar
Ohta, S.-I., Markov type of Alexandrov spaces of non-negative curvature. Mathematika 55(1–2) 2009, 177–189.10.1112/S0025579300001005Google Scholar
Ohta, S.-I. and Pichot, M., A note on Markov type constants. Arch. Math. (Basel) 92(1) 2009, 80–88.10.1007/s00013-008-2672-2Google Scholar
Petrunin, A., Puzzles in geometry that I know and love. Preprint, 2009, arXiv:0906.0290.Google Scholar
Terng, C.-L. and Thorbergsson, G., Submanifold geometry in symmetric spaces. J. Differential Geom. 42(3) 1995, 665–718.10.4310/jdg/1214457552Google Scholar
Zolotov, V., Dimension of a snowflake of a finite Euclidean subspace. Preprint, 2017, arXiv:1706.09998.Google Scholar
Zolotov, V., Markov type constants, flat tori and Wasserstein spaces. Geom. Dedicata 195(1) 2018, 249–263.10.1007/s10711-017-0287-0Google Scholar