Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-11T01:52:59.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Fractal series

Part of: Classical measure theory

Published online by Cambridge University Press:  26 February 2010

M. Morán
M. Morán
Affiliation:
Departamento de Analisis Economico, Universidad Complutense, Campus de Somosaguas, E-28023 Madrid, Spain.
Get access

Extract

Introduction. This paper describes a natural way to associate fractal setsto a certain class of absolutely convergent series in 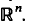In Theorem 1 we give sufficient conditions for such series. Theorem 2 shows that each analytic function gives a different fractal series for each number in a certain open set. Theorem 3 gives the Hausdorff dimension of the associated sets to fractal series, under suitable conditions on the series. This theorem can be applied to some standard series in analysis, such as the binomial, exponential and trigonometrical complex series. The associated sets to geometrical complex series are selfsimilar sets previously studied by M. F. Barnsley from a different (dynamical) point of view (see refs. [5], [6]).

MSC classification

Secondary: 28A75: Length, area, volume, other geometric measure theory
Type
Research Article
Information
Mathematika , Volume 36 , Issue 2 , December 1989 , pp. 334 - 348
Copyright
Copyright © University College London 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Falconer, K. J.. The Geometry of Fractal Sets (Cambridge University Press, 1985).CrossRefGoogle Scholar
2.Mattila, P.. Lecture Notes on Geometric Measure Theory (Universidad de Extremadura, 1986).Google Scholar
3.Rogers, C. A.. Hausdorff Measures (Cambridge University Press, 1970).Google Scholar
4.Guzman, M. de. Real Variable Methods in Fourier Analysis (North Holland, 1981).Google Scholar
5.Barnsley, M. F. and Harrington, A. N.. A Mandelbrot Set for Pairs of Linear Maps. Physica, 15D (1985).Google Scholar
6.Barnsley, M. F.. Fractals Everywhere (Academic Press, 1988).Google Scholar
7.Morán, M.. Ph.D. Thesis (Universidad Complutense de Madrid, 1988).Google Scholar