FROM KHINCHIN’S CONJECTURE ON STRONG UNIFORMITY TO SUPERUNIFORM MOTIONS

Abstract

We attempt to develop a new chapter of the theory of uniform distribution; we call it strong uniformity. Strong uniformity in a nutshell means that we combine Lebesgue measure with the classical theory of uniform distribution, basically founded by Weyl in his famous paper from 1916 [Über die Gleichverteilung von Zahlen mod Eins, Math. Ann.77 (1916), 313–352], which is built around nice test sets, such as axis-parallel rectangles and boxes. We prove the continuous version of the well-known Khinchin’s conjecture [Eins Satz über Kettenbrüche mit arithmetischen Adwendungen, Math. Z.18 (1923), 289–306] in every dimension 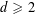$d\geqslant 2$ (the discrete version turned out to be false—it was disproved by Marstrand [On Khinchin’s conjecture about strong uniform distribution, Proc. Lond. Math. Soc. (3) 21 (1970), 540–556]). We consider an arbitrarily complicated but fixed measurable test set $S$ in the 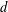$d$-dimensional unit cube, and study the uniformity of a typical member of some natural families of curves, such as all torus lines or billiard paths starting from the origin, with respect to 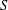$S$. In the two-dimensional case we have the very surprising superuniformity of the typical torus lines and billiard paths. In dimensions 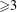${\geqslant}3$ we still have strong uniformity, but not superuniformity. However, in dimension three we have the even more striking super-duper uniformity for two-dimensional rays (replacing the torus lines). Finally, we indicate how to exhibit superuniform motions on every “reasonable” plane region (e.g., the circular disk) and on every “reasonable” closed surface (sphere, torus and so on).