Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T21:31:26.470Z Has data issue: false hasContentIssue false
  • English
  • Français

A functional analytic interpretation of the number of faces of a polyhedron

Part of: Polytopes and polyhedra

Published online by Cambridge University Press:  26 February 2010

Krzysztof Przesławski
Krzysztof Przesławski
Affiliation:
Instytut Matematyki, Uniwersytet Zielonogórski, ul. Podgórna 50, 65–246, Zielona Góra, Poland. E-mail: k.przeslawski@im.pz.zgora.pl
Get access

Extract

Let P⊂ℝ2 be a polyhedron, that is, the intersection of a finite number of closed half-spaces, and suppose that its characteristic function lP can be expressed as a linear combination

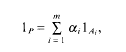
where each Ai is a relatively open and convex set. Let n(P) be the number of all non-empty facets of P. One of the main objectives of this paper is to show that

MSC classification

Secondary: 52B05: Combinatorial properties (number of faces, shortest paths, etc.)
Type
Research Article
Information
Mathematika , Volume 47 , Issue 1-2 , December 2000 , pp. 1 - 7
Copyright
Copyright © University College London 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Groemer, H.. Minkowski addition and mixed volumes. Geom. Dedicata 4 (1975), 91–104.Google Scholar
2.McMullen, P. and Schneider, R.. Valuations on convex bodies. In Convexity and its Applications (ed. Gruber, P. M. and Wills, J. M.), Birkhäuser (Basel, 1983), 170–247.CrossRefGoogle Scholar
3.Morelli, R.. A theory of polyhedra. Advances Math. 97 (1993), 1–73.CrossRefGoogle Scholar
4.Przeslawski, K.. Linear algebra of convex sets and the Euler characteristic. Linear and Multi linear Algebra 31 (1992), 153–191.CrossRefGoogle Scholar
5.Pukhlikov, A. V. and Khovanskil, A. G.. Finitely additive measures of virtual polytopes (Russian). Algebra i Analiz 4 (1992), 161–185. (English translation: St. Petersburg Math. J. 4(1993), 337-356.)Google Scholar