Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T22:05:03.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Indefinite quadratic polynomials

Published online by Cambridge University Press:  26 February 2010

G. L. Watson
G. L. Watson
Affiliation:
University College, London, W.C.I.
Get access

Extract

1. Let f = f(x1, …, xn) be an indefinite quadratic form in n variables with discriminant d = d(f) ¹ 0; and let ξ1, …, ξn be real numbers. We consider how closely the inhomogeneous quadratic polynomial

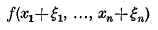
can be made to approximate to a given real number α by choice of suitable integral values of the variables xi. The best that is known seems to be that the inequalities

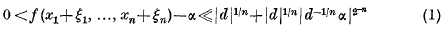
can always be satisfied if the implied constant is given a suitable value depending only on n. For α ≥ 0 this is a restatement of a result proved by Dr. D. M. E. Foster.

Type
Research Article
Information
Mathematika , Volume 7 , Issue 2 , December 1960 , pp. 141 - 144
Copyright
Copyright © University College London 1960

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 141 note * Mathematika, 3 (1956), 111–116CrossRefGoogle Scholar, Theorem 1.

page 141 note † See Ridout, D., Mathematika, 5 (1958), 122–124CrossRefGoogle Scholar, for references and proof of one outstanding case.

page142 note * Oppenheim, A., Monatshefte für Mathematik, 57 (1954), 97–101CrossRefGoogle Scholar; the writer outlines an alternative proof found independently by Heilbronn, which appears not to have been published.

page142 note † Oppenheim, A., Quart. J. Math. Oxford (2), 4 (1953), 54–59 (54, Theorem 1).CrossRefGoogle Scholar

page143 note * Diophantische Approximationen (Ergebnisse der Mathematik und ihrer Grenzgebiete) (New York), 93, Satz 10.Google Scholar