Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T21:53:42.802Z Has data issue: false hasContentIssue false
  • English
  • Français

Isomorphic Koszul complexes

Published online by Cambridge University Press:  26 February 2010

D. Kirby
D. Kirby
Affiliation:
The University, Southampton.
Get access

Extract

Let a1 …, ar be elements of a commutative ring R with identity. When the R-length of

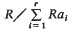
is finite and R is Noetherian the multiplicity e(a1 …, ar\R) can be defined in one of three ways. Starting either from the earliest definition by means of Hilbert functions (see Samuel [4]) or from the latest by induction on r(see Wright [5]) it can be shown that e(a1 …, ar\R) depends only on the ideal

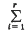
and the number r of generators. The other definition due to Auslander and Buchsbaum [1] is as the Euler-Poincare characteristic of a Koszul complex. The main purpose of this note is to investigate the extent to which the separate homology modules and the Koszul complex itself are independent of the sequence a1 …, ar. First it is shown that when A = (a1, …, ar) and B = (b1 …, br) are related by a reversible R-linear transformation the two Koszul complexes are isomorphic. A special case of the final theorem states that if A and B are minimal generating sets of the same ideal and R is a local ring then again the Koszul complexes are isomorphic.

Type
Research Article
Information
Mathematika , Volume 20 , Issue 1 , June 1973 , pp. 53 - 58
Copyright
Copyright © University College London 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Auslander, M. and Buchsbaum, D. A., “Codimension and multiplicity”, Ann. of Math., 68 (1958), 625–657.CrossRefGoogle Scholar
2. Buchsbaum, D. A., “Complexes associated with the minors of a matrix”, Symposia Math., 4 (1970), 255–283.Google Scholar
3. Northcott, D. G., “Duality and the theory of complexes”, Proc. London Math. Soc, 23 (1971), 577–592.Google Scholar
4. Samuel, P., “Sur la notion de multiplicityé en alg–bre et en g–ometrie algébrique”, J. Math, pure et appl., 30 (1951), 159–174.Google Scholar
5. Wright, D. J., “General multiplicity theory”, Proc. London Math. Soc, 15 (1965), 269–288.CrossRefGoogle Scholar