Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T21:42:54.290Z Has data issue: false hasContentIssue false
  • English
  • Français

LARGE BIAS FOR INTEGERS WITH PRIME FACTORS IN ARITHMETIC PROGRESSIONS

Part of: Multiplicative number theory Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  15 February 2018

Xianchang Meng
Xianchang Meng*
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, 1409 West Green Street, Urbana, IL 61801, U.S.A. email xmeng13@illinois.edu
Get access

Abstract

We prove asymptotic formulas for the number of integers at most $x$ that can be written as the product of 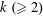$k~({\geqslant}2)$ distinct primes 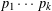$p_{1}\cdots p_{k}$ with each prime factor in an arithmetic progression 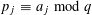$p_{j}\equiv a_{j}\hspace{0.2em}{\rm mod}\hspace{0.2em}q$, 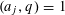$(a_{j},q)=1$ 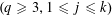$(q\geqslant 3,1\leqslant j\leqslant k)$. For any 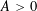$A>0$, our result is uniform for 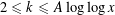$2\leqslant k\leqslant A\log \log x$. Moreover, we show that there are large biases toward certain arithmetic progressions 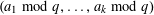$(a_{1}\hspace{0.2em}{\rm mod}\hspace{0.2em}q,\ldots ,a_{k}\hspace{0.2em}{\rm mod}\hspace{0.2em}q)$, and such biases have connections with Mertens’ theorem and the least prime in arithmetic progressions.

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$ 11N13: Primes in progressions 11N69: Distribution of integers in special residue classes
Type
Research Article
Information
Mathematika , Volume 64 , Issue 1 , 2018 , pp. 237 - 252
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, A., Birch, B. J. and Wirsing, E. A., On a problem of Chowla, On a problem of Chowla. J. Number Theory 5 1973, 224–236.CrossRefGoogle Scholar
Davenport, H., Multiplicative Number Theory, 3rd edn. (Graduate Texts in Mathematics 74 ), Springer (New York, Berlin, 2000).Google Scholar
Dummit, D., Granville, A. and Kisilevsky, H., Big biases amongst products of two primes. Mathematika 62 2016, 502–507.CrossRefGoogle Scholar
Ebeling, W., Functions of Several Complex Variables and their Singularities (Graduate Studies in Mathematics 83 ), American Mathematical Society (Providence, RI, 2007).CrossRefGoogle Scholar
Ford, K. and Sneed, J., Chebyshev’s bias for products of two primes. Experiment. Math. 19(4) 2010, 385–398.CrossRefGoogle Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 5th edn. Oxford University Press (Oxford, 1979).Google Scholar
Hough, P., A lower bound for biases amongst products of two primes. Preprint, 2016,arXiv:1610.01943.CrossRefGoogle Scholar
Karatsuba, A. A., Basic Analytic Number Theory, Springer (Berlin, Heidelberg, 1993).CrossRefGoogle Scholar
Kolesnik, G., On the order of Dirichlet L-functions. Pacific J. Math. 82(2) 1979, 479–484.CrossRefGoogle Scholar
Languasco, A. and Zaccagnini, A., Computing the Mertens’ and Meissel-Mertens’ constants for sums over arithmetic progressions. Experiment. Math. 19(3) 2010, 279–284.CrossRefGoogle Scholar
Languasco, A. and Zaccagnini, A., Computation of the Mertens and Meissel–Mertens constants for sums over arithmetic progressions, http://www.math.unipd.it/∼languasc/Mertens-comput.html.Google Scholar
Meng, X., Chebyshev’s bias for products of $k$ primes. Preprint, 2016, arXiv:1606.04877.Google Scholar
Mertens, F., Ein beitrag zur analytischen zahlentheorie. J. Reine Angew. Math. 78 1874, 46–62.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory I Classical Theory (Graduate Studies in Advanced Mathematics 97 ), Cambridge University Press (Cambridge, 2007).Google Scholar
Moree, P., Chebyshev’s bias for composite numbers with restricted prime divisors. Math. Comp. 73(245) 2003, 425–449.CrossRefGoogle Scholar
Murty, M. R. and Murty, V. K., A problem of Chowla revisited. J. Number Theory 131(9) 2011, 1723–1733.CrossRefGoogle Scholar
Murty, M. R. and Rath, P., Transcendental Numbers, Springer (New York, 2014).CrossRefGoogle Scholar
Norton, K., On the number of restricted prime factors of an integer I. Illinois J. Math. 20(4) 1976, 681–705.CrossRefGoogle Scholar
Pomerance, C., On the distribution of amicable numbers. J. Reine Angew. Math. 293/294 1977, 217–222.Google Scholar
Tenenbaum, G., Introduction to Analytic and Probabilistic Number Theory, 3rd edn. (Graduate Studies in Mathematics 163 ), American Mathematical Society (Providence, RI, 2015).CrossRefGoogle Scholar