Article contents
LARGE MOMENTS AND EXTREME VALUES OF CLASS NUMBERS OF INDEFINITE BINARY QUADRATIC FORMS
Published online by Cambridge University Press: 20 April 2017
Abstract
Let 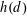 $h(d)$ be the class number of indefinite binary quadratic forms of discriminant
$h(d)$ be the class number of indefinite binary quadratic forms of discriminant 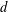 $d$ and let
$d$ and let 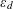 $\unicode[STIX]{x1D700}_{d}$ be the corresponding fundamental unit. In this paper, we obtain an asymptotic formula for the
$\unicode[STIX]{x1D700}_{d}$ be the corresponding fundamental unit. In this paper, we obtain an asymptotic formula for the 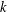 $k$ th moment of
$k$ th moment of 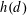 $h(d)$ over positive discriminants
$h(d)$ over positive discriminants 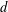 $d$ with
$d$ with 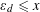 $\unicode[STIX]{x1D700}_{d}\leqslant x$ , uniformly for real numbers
$\unicode[STIX]{x1D700}_{d}\leqslant x$ , uniformly for real numbers 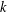 $k$ in the range
$k$ in the range 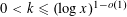 $0<k\leqslant (\log x)^{1-o(1)}$ . This improves upon the work of Raulf, who obtained such an asymptotic for a fixed positive integer
$0<k\leqslant (\log x)^{1-o(1)}$ . This improves upon the work of Raulf, who obtained such an asymptotic for a fixed positive integer 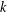 $k$ . We also investigate the distribution of large values of
$k$ . We also investigate the distribution of large values of 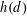 $h(d)$ when the discriminants
$h(d)$ when the discriminants 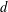 $d$ are ordered according to the size of their fundamental units
$d$ are ordered according to the size of their fundamental units 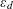 $\unicode[STIX]{x1D700}_{d}$ . In particular, we show that the tail of this distribution has the same shape as that of class numbers of imaginary quadratic fields ordered by the size of their discriminants. As an application of these results, we prove that there are many positive discriminants
$\unicode[STIX]{x1D700}_{d}$ . In particular, we show that the tail of this distribution has the same shape as that of class numbers of imaginary quadratic fields ordered by the size of their discriminants. As an application of these results, we prove that there are many positive discriminants 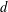 $d$ with class number
$d$ with class number 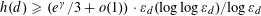 $h(d)\geqslant (e^{\unicode[STIX]{x1D6FE}}/3+o(1))\cdot \unicode[STIX]{x1D700}_{d}(\log \log \unicode[STIX]{x1D700}_{d})/\log \,\unicode[STIX]{x1D700}_{d}$ , a bound that we believe is best possible. We also obtain an upper bound for
$h(d)\geqslant (e^{\unicode[STIX]{x1D6FE}}/3+o(1))\cdot \unicode[STIX]{x1D700}_{d}(\log \log \unicode[STIX]{x1D700}_{d})/\log \,\unicode[STIX]{x1D700}_{d}$ , a bound that we believe is best possible. We also obtain an upper bound for 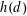 $h(d)$ that is twice as large, assuming the generalized Riemann hypothesis.
$h(d)$ that is twice as large, assuming the generalized Riemann hypothesis.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2017
References
- 1
- Cited by

