Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T22:57:57.183Z Has data issue: false hasContentIssue false
  • English
  • Français

LARGE VALUES OF 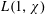$L(1,\unicode[STIX]{x1D712})$ FOR 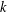$k$TH ORDER CHARACTERS 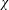$\unicode[STIX]{x1D712}$ AND APPLICATIONS TO CHARACTER SUMS

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  26 July 2016

Youness Lamzouri
Youness Lamzouri*
Affiliation:
Department of Mathematics and Statistics, York University, 4700 Keele Street, Toronto, ON, M3J1P3, Canada email lamzouri@mathstat.yorku.ca
Get access

Abstract

For any given integer 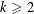$k\geqslant 2$ we prove the existence of infinitely many 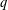$q$ and characters 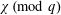$\unicode[STIX]{x1D712}\,(\text{mod}\;q)$ of order 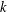$k$ such that 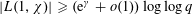$|L(1,\unicode[STIX]{x1D712})|\geqslant (\text{e}^{\unicode[STIX]{x1D6FE}}+o(1))\log \log q$. We believe this bound to be the best possible. When the order 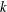$k$ is even, we obtain similar results for 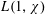$L(1,\unicode[STIX]{x1D712})$ and 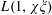$L(1,\unicode[STIX]{x1D712}\unicode[STIX]{x1D709})$, where 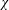$\unicode[STIX]{x1D712}$ is restricted to even (or odd) characters of order 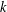$k$ and 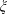$\unicode[STIX]{x1D709}$ is a fixed quadratic character. As an application of these results, we exhibit large even-order character sums, which are likely to be optimal.

MSC classification

Primary: 11M20: Real zeros of $L(s, chi)$; results on $L(1, chi)$ 11M06: $zeta (s)$ and $L(s, chi)$
Type
Research Article
Information
Mathematika , Volume 63 , Issue 1 , 2017 , pp. 53 - 71
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baier, S. and Young, M. P., Mean values with cubic characters. J. Number Theory 130(4) 2010, 879–903.CrossRefGoogle Scholar
Bateman, P. T. and Chowla, S., Averages of character sums. Proc. Amer. Math. Soc. 1 1950, 781–787.Google Scholar
Blomer, V., Goldmakher, L. and Louvel, B., L-functions with nth-order twists. Int. Math. Res. Not. IMRN 2014(7), 1925–1955.Google Scholar
Bober, J., Averages of character sums. Preprint, 2014, arXiv:1409.1840.Google Scholar
Bober, J., Goldmakher, L., Granville, A. and Koukoulopoulos, D., The frequency and the structure of large character sums. Preprint, 2014, arXiv:1410.8189.Google Scholar
Chowla, S., Improvement of a theorem of Linnik and Walfisz. Proc. Lond. Math. Soc. (3) 50 1949, 423–429.Google Scholar
Elliott, P. D. T. A., On the mean value of f (p). Proc. Lond. Math. Soc. (3) 21 1970, 28–96.Google Scholar
Gao, P. and Zhao, L., Large sieve inequalities for quartic characters. Q. J. Math. 63(4) 2012, 891–917.Google Scholar
Goldmakher, L., Multiplicative mimicry and improvements to the Pólya–Vinogradov inequality. Algebr. Number Theory 6(1) 2012, 123–163.Google Scholar
Goldmakher, L. and Lamzouri, Y., Lower bounds on odd order character sums. Int. Math. Res. Not. IMRN 2012 (21) 2012, 5006–5013.Google Scholar
Goldmakher, L. and Lamzouri, Y., Large even order character sums. Proc. Amer. Math. Soc. 142(8) 2014, 2609–2614.Google Scholar
Granville, A. and Soundararajan, K., The distribution of values of L (1, 𝜒 d ). Geom. Funct. Anal. 13(5) 2003, 992–1028.CrossRefGoogle Scholar
Granville, A. and Soundararajan, K., Extreme values of |𝜁(1 + it)|. In The Riemann Zeta Function and Related Themes: Papers in Honour of Professor K. Ramachandra (Ramanujan Mathematical Society Lecture Notes Series 2 ), Ramanujan Mathematical Society (Mysore, 2006), 65–80.Google Scholar
Granville, A. and Soundararajan, K., Large character sums: pretentious characters and the Pólya–Vinogradov theorem. J. Amer. Math. Soc. 20(2) 2007, 357–384.Google Scholar
Heath-Brown, D. R., Kummer’s conjecture for cubic Gauss sums. Israel J. Math. 120(part A) 2000, 97–124.Google Scholar
Littlewood, J. E., On the class number of the corpus P (√-k). Proc. Lond. Math. Soc. (3) 27 1928, 358–372.CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., Exponential sums with multiplicative coefficients. Invent. Math. 43(1) 1977, 69–82.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Extreme values of Dirichlet L-functions at 1. In Number Theory in Progress, Vol. 2 (Zakopane-Kościelisko, 1997), de Gruyter (Berlin, 1999), 1039–1052.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory. I. Classical Theory (Cambridge Studies in Advanced Mathematics 97 ), Cambridge University Press (Cambridge, 2007).Google Scholar
Paley, R. E. A. C., A theorem on characters. J. Lond. Math. Soc. (2) 7 1932, 28–32.Google Scholar
Pólya, G., Uber die Verteilung der quadratischen Reste und Nichtreste. Göttingen Nachrichten 1918, 21–29.Google Scholar
Vinogradov, I. M., Uber die Verteilung der quadratischen Reste und Nichtreste. J. Soc. Phys. Math. Univ. Permi (2) 1919, 1–14.Google Scholar