Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T21:43:27.307Z Has data issue: false hasContentIssue false
  • English
  • Français

THE LARGE-TIME DEVELOPMENT OF THE SOLUTION TO AN INITIAL-VALUE PROBLEM FOR THE KORTEWEG–DE VRIES EQUATION. II. INITIAL DATA HAS A DISCONTINUOUS COMPRESSIVE STEP

Part of: Infinite-dimensional Hamiltonian systems

Published online by Cambridge University Press:  14 May 2014

J. A. Leach  and
D. J. Needham
J. A. Leach
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham B15 2TT,U.K. email D.J.Needham@bham.ac.uk
D. J. Needham
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham B15 2TT,U.K. email J.A.Leach@bham.ac.uk
Get access

Abstract

In this paper, we consider an initial-value problem for the Korteweg–de Vries equation. The normalized Korteweg–de Vries equation considered is given by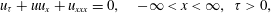

$$\begin{equation*} u_{\tau }+u u_{x}+u_{xxx}=0, \quad -\infty <x<\infty ,\ \tau >0, \end{equation*}$$
where $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x$ and $\tau $ represent dimensionless distance and time, respectively. In particular, we consider the case when the initial data has a discontinuous compressive step, where 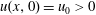$u(x,0) =u_{0}>0$ for 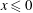$x \le 0$ and 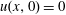$u(x,0)=0$ for 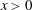$x>0$. The method of matched asymptotic coordinate expansions is used to obtain the detailed large-$\tau $ asymptotic structure of the solution to this problem, which exhibits the formation of a dispersive shock wave.

MSC classification

Secondary: 37K40: Soliton theory, asymptotic behavior of solutions
Type
Research Article
Information
Mathematika , Volume 60 , Issue 2 , July 2014 , pp. 391 - 414
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ablowitz, M. J. and Baldwin, D. E., Interactions and asymptotics of dispersive shock waves—Korteweg–de Vries equation. Phys. Lett. A 377(7) 2013, 555–559.Google Scholar
Egorova, I., Gladka, Z., Kotlyarov, V. and Teschl, G., Long-time asymptotics for the Korteweg–de Vries equation with step-like initial data. Nonlinearity 26 2013, 1839–1864.Google Scholar
Fornberg, B. and Whitham, G. B., A numerical and theoretical study of certain nonlinear wave phenomena. Phil. Trans. R. Soc. Lond. 289 1978, 373–404.Google Scholar
Gurevich, A. V. and Pitaevskii, L. P., Decay of initial discontinuity in the Korteweg–de Vries equation. Zh. Eksp. Teor. Fiz. Pis. Red. 17(5) 1973, 268–271.Google Scholar
Hastings, S. P. and McLeod, J. B., A boundary value problem associated with the second Painlevé transcendent and the Korteweg–de Vries equation. Arch. Ration Mech. Anal. 73 1980, 31–51.Google Scholar
Khruslov, E. Y., Asymptotics of the solution of the Cauchy problem for the Korteweg–de Vries equation with initial data of step type. Mat. Sb. (N. S.) 99 1976, 261–281.Google Scholar
Khruslov, E. Y. and Stephan, H., Splitting of some nonlocalized solutions of the Korteweg–de Vries equation into solitons. Mat. Fiz. Anal. Geom. 5 1998, 12.Google Scholar
Leach, J. A., The large-time development of the solution to an initial-boundary value problem for the Korteweg–de Vries equation. I. Steady state solutions. J. Differential Equations 246 2009, 3681–3703.Google Scholar
Leach, J. A., The large-time development of the solution to an initial-boundary value problem for the Korteweg–de Vries equation on the negative quarter-plane. J. Differential Equations 247 2009, 1206–1228.CrossRefGoogle Scholar
Leach, J. A. and Needham, D. J., The large-time development of the solution to an initial-value problem for the Korteweg–de Vries equation. I. Initial data has a discontinuous expansive step. Nonlinearity 21 2008, 2391–2408.CrossRefGoogle Scholar
Leach, J. A. and Needham, D. J., Matched Asymptotic Expansions in Reaction-Diffusion Theory, Springer (London, 2003).Google Scholar
Whitham, G. B., Non-linear dispersive waves. Proc. R. Soc. Lond. A283 1965, 238–291.Google Scholar