Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T03:47:55.722Z Has data issue: false hasContentIssue false
  • English
  • Français

LEVEL RECIPROCITY IN THE TWISTED SECOND MOMENT OF RANKIN–SELBERG 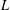$L$-FUNCTIONS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  26 June 2018

Nickolas Andersen  and
Eren Mehmet Kıral
Nickolas Andersen
Affiliation:
UCLA Mathematics Department, Los Angeles, CA 90095, U.S.A. email nandersen@math.ucla.edu
Eren Mehmet Kıral
Affiliation:
Wako-Shi, Saitama, Japan email erenmehmetkiral@protonmail.com
Get access

Abstract

We prove an exact formula for the second moment of Rankin–Selberg 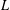$L$-functions 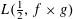$L(\frac{1}{2},f\times g)$ twisted by 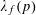$\unicode[STIX]{x1D706}_{f}(p)$, where 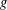$g$ is a fixed holomorphic cusp form and 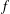$f$ is summed over automorphic forms of a given level 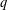$q$. The formula is a reciprocity relation that exchanges the twist parameter 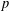$p$ and the level 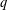$q$. The method involves the Bruggeman–Kuznetsov trace formula on both ends; finally the reciprocity relation is established by an identity of sums of Kloosterman sums.

MSC classification

Primary: 11F03: Modular and automorphic functions 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations 11F72: Spectral theory; Selberg trace formula
Type
Research Article
Information
Mathematika , Volume 64 , Issue 3 , 2018 , pp. 770 - 784
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This material is based upon work supported by the National Science Foundation under Grant No. 1440140, while the authors were in residence at the Mathematical Sciences Research Institute in Berkeley, California, during the Spring semester of 2017. The first author is also supported by NSF grant DMS-1701638.

References

Bettin, S., On the reciprocity law for the twisted second moment of Dirichlet L-functions. Trans. Amer. Math. Soc. 368(10) 2016, 6887–6914.Google Scholar
Blomer, V. and Khan, R., Twisted moments of $L$ -functions and spectral reciprocity. Preprint, 2017,arXiv:1706.01245.Google Scholar
Blomer, V., Li, X. and Miller, S. D., A spectral reciprocity formula and non-vanishing for $L$ -functions on $\text{GL}(4)\times \text{GL}(2)$ . Preprint, 2017, arXiv:1705.04344.Google Scholar
Conrey, J. B., The mean-square of Dirichlet L-functions. Preprint, 2007, arXiv:0708.2699.Google Scholar
Ivić, A. and Motohashi, Y., On the fourth power moment of the Riemann zeta-function. J. Number Theory 51(1) 1995, 16–45.Google Scholar
Iwaniec, H., Topics in Classical Automorphic Forms (Graduate Studies in Mathematics 17 ), American Mathematical Society (Providence, RI, 1997).Google Scholar
Iwaniec, H., Spectral Methods of Automorphic Forms, Vol. 53, American Mathematical Society (Providence, RI, 2002).Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory (Colloquium Publications 53 ), American Mathematical Society (Providence, RI, 2004).Google Scholar
Kıral, E. M. and Young, M. P., The fifth moment of modular $L$ -functions. Preprint, 2017,arXiv:1701.07507.Google Scholar
Motohashi, Y., An explicit formula for the fourth power mean of the Riemann zeta-function. Acta Math. 170(2) 1993, 181–220.Google Scholar
Motohashi, Y., A functional equation for the spectral fourth moment of modular Hecke L-functions. In Proceedings of the Session in Analytic Number Theory and Diophantine Equations (Bonner Mathematische Schriften 360 ), University of Bonn (Bonn, 2003), 19.Google Scholar
Petrow, I. N., A twisted Motohashi formula and Weyl-subconvexity for L-functions of weight two cusp forms. Math. Ann. 363(1–2) 2015, 175–216.Google Scholar
Young, M. P., The fourth moment of Dirichlet L-functions. Ann. of Math. (2) 173(1) 2011, 1–50.Google Scholar
Young, M. P., The reciprocity law for the twisted second moment of Dirichlet L-functions. Forum Math. 23(6) 2011, 1323–1337.Google Scholar