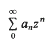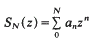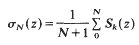Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Katsoprinakis, E. S.
and
Nestoridis, V.
1994.
An application of Kronecker's theorem to rational functions.
Mathematische Annalen,
Vol. 298,
Issue. 1,
p.
145.
Nestoridis, V.
1994.
Distribution of partial sums of the Taylor development of rational functions.
Transactions of the American Mathematical Society,
Vol. 346,
Issue. 1,
p.
283.
Nestoridis, V.
2018.
Universal Taylor Series Without Baire and the Influence of J.-P. Kahane.
Analysis Mathematica,
Vol. 44,
Issue. 2,
p.
237.