Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T21:37:19.885Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCAL AVERAGE OF THE HYPERBOLIC CIRCLE PROBLEM FOR FUCHSIAN GROUPS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  06 February 2018

András Biró
András Biró*
Affiliation:
A. Rényi Institute of Mathematics, Hungarian Academy of Sciences, Reáltanoda u. 13–15, 1053 Budapest, Hungary email biroand@renyi.hu
Get access

Abstract

Let 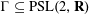$\unicode[STIX]{x1D6E4}\subseteq \operatorname{PSL}(2,\mathbf{R})$ be a finite-volume Fuchsian group. The hyperbolic circle problem is the estimation of the number of elements of the 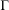$\unicode[STIX]{x1D6E4}$-orbit of $z$ in a hyperbolic circle around 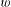$w$ of radius 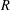$R$, where $z$ and 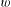$w$ are given points of the upper half plane and 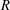$R$ is a large number. An estimate with error term 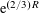$\text{e}^{(2/3)R}$ is known, and this has not been improved for any group. Recently, Risager and Petridis proved that in the special case 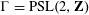$\unicode[STIX]{x1D6E4}=\operatorname{PSL}(2,\mathbf{Z})$ taking 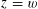$z=w$ and averaging over $z$ in a certain way the error term can be improved to 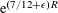$\text{e}^{(7/12+\unicode[STIX]{x1D716})R}$. Here we show such an improvement for a general 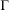$\unicode[STIX]{x1D6E4}$; our error term is 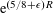$\text{e}^{(5/8+\unicode[STIX]{x1D716})R}$ (which is better than 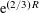$\text{e}^{(2/3)R}$ but weaker than the estimate of Risager and Petridis in the case 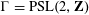$\unicode[STIX]{x1D6E4}=\operatorname{PSL}(2,\mathbf{Z})$). Our main tool is our generalization of the Selberg trace formula proved earlier.

MSC classification

Primary: 11F72: Spectral theory; Selberg trace formula
Type
Research Article
Information
Mathematika , Volume 64 , Issue 1 , 2018 , pp. 159 - 183
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Biró, A., On a generalization of the Selberg trace formula. Acta Arith. 87(4) 1999, 319–338.Google Scholar
Biró, A., A relation between triple products of weight 0 and weight 1/2 cusp forms. Israel J. Math. 182(1) 2011, 61–101.Google Scholar
Chamizo, F., Some applications of large sieve in Riemann surfaces. Acta Arith. 77(4) 1996, 315–337.Google Scholar
Fay, J. D., Fourier coefficients of the resolvent for a Fuchsian group. J. Reine Angew. Math. 294 1977, 143–203.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Tables of Integrals, Series and Products, 6th edn., Academic Press (New York, 2000).Google Scholar
Hejhal, D. A., The Selberg Trace Formula for PSL(2, R), Vol. 2, (Lecture Notes in Mathematics 1001 ), Springer (New York, 1983).Google Scholar
Horn, R. A. and Johnson, C. R., Matrix Analysis, Cambridge University Press (Cambridge, 1985).Google Scholar
Huber, H., Ein Gitterpunktproblem in der hyperbolischen Ebene. J. Reine Angew. Math. 496 1998, 15–53.Google Scholar
Iwaniec, H., Introduction to the Spectral Theory of Automorphic Forms, Revista Matemática Iberoamericana (Madrid, 1995).Google Scholar
Kuipers, L. and Niederreiter, H., Uniform Distribution of Sequences, Wiley (New York, 1974).Google Scholar
Risager, M. and Petridis, Y., Local average in hyperbolic lattice point counting, with an appendix by Niko Laaksonen. Math. Z. 2016, doi:10.1007/s00209-016-1749-z.Google Scholar
Zelditch, S., Selberg trace formulae, pseudodifferential operators, and geodesic periods of automorphic forms. Duke Math. J. 56(2) 1988, 295–344.Google Scholar
Zelditch, S., Trace formula for compact 𝛤 \backslash PSL(2, R) and the equidistribution theory of closed geodesics. Duke Math. J. 59(1) 1989, 27–81.Google Scholar
Zelditch, S., Selberg trace formulae and equidistribution theorems for closed geodesics and Laplace eigenfunctions: finite area surfaces. Mem. Amer. Math. Soc. 96(465) 1992.Google Scholar