Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T15:42:52.632Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MIXED SCHMIDT CONJECTURE IN THE THEORY OF DIOPHANTINE APPROXIMATION

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  10 June 2011

Dzmitry Badziahin ,
Jason Levesley  and
Sanju Velani
Dzmitry Badziahin
Affiliation:
Department of Mathematics, University of York, Heslington, York, YO10 5DD, U.K. (email: db528@york.ac.uk)
Jason Levesley
Affiliation:
Department of Mathematics, University of York, Heslington, York, YO10 5DD, U.K. (email: jl107@york.ac.uk)
Sanju Velani
Affiliation:
Department of Mathematics, University of York, Heslington, York, YO10 5DD, U.K. (email: slv3@york.ac.uk)
Get access

Abstract

Let 𝒟=(dn)∞n=1 be a sequence of integers with dn≥2, and let (i,j) be a pair of strictly positive numbers with i+j=1. We prove that the set of x∈ℝ for which there exists some constant c(x)≧0 such that 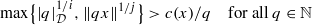is one-quarter winning (in the sense of Schmidt games). Thus the intersection of any countable number of such sets is of full dimension. This, in turn, establishes the natural analogue of Schmidt’s conjecture within the framework of the de Mathan–Teulié conjecture, also known as the “mixed Littlewood conjecture”.

MSC classification

Secondary: 11K60: Diophantine approximation 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension
Type
Research Article
Information
Mathematika , Volume 57 , Issue 2 , July 2011 , pp. 239 - 245
Copyright
Copyright © University College London 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Badziahin, D., Pollington, A. and Velani, S., On a problem in simultaneously Diophantine approximation: Schmidt’s conjecture. Ann. of Math. (2) (to appear). Preprint, 2010, arXiv:1001.2694.Google Scholar
[2]Bugeaud, Y., Drmota, M. and de Mathan, B., On a mixed Littlewood conjecture in Diophantine approximation. Acta Arith. 128(2) (2007), 107–124; MR 2313997(2008d:11067).CrossRefGoogle Scholar
[3]Bugeaud, Y., Haynes, A. and Velani, S., Metric considerations concerning the mixed Littlewood conjecture. Int. J. Number Theory (to appear). Preprint, 2009, arXiv:0909.3923v1.Google Scholar
[4]Bugeaud, Y. and Moshchevitin, N., Badly approximable numbers and Littlewood-type problems. Math. Proc. Cambridge Philos. Soc. 150 (2011), 215–226.CrossRefGoogle Scholar
[5]Einsiedler, M., Katok, A. and Lindenstrauss, E., Invariant measures and the set of exceptions to Littlewood’s conjecture. Ann. of Math. (2) 164(2) (2006), 513–560; MR 2247967(2007j:22032).CrossRefGoogle Scholar
[6]Einsiedler, M. and Kleinbock, D., Measure rigidity and p-adic Littlewood-type problems. Compositio Math. 143(3) (2007), 689–702; MR 2330443(2008f:11076).CrossRefGoogle Scholar
[7]Harrap, S. and Yusupova, T., On a mixed Khintchine problem in Diophantine approximation, in preparation.Google Scholar
[8]de Mathan, B. and Teulié, O., Problèmes diophantiens simultanés. Monatsh. Math. 143(3) (2004), 229–245; MR 2103807(2005h:11147).CrossRefGoogle Scholar
[9]Pollington, A. and Velani, S., On a problem in simultaneously Diophantine approximation: Littlewood’s conjecture. Acta Math. 66 (2000), 29–40; MR 1819996(2002a:11076).Google Scholar
[10]Schmidt, W. M., On badly approximable numbers and certain games. Trans. Amer. Math. Soc. 123 (1966), 178–199; MR 0195595(33#3793).CrossRefGoogle Scholar
[11]Schmidt, W. M., Open problems in Diophantine approximation. In Approximations diophantiennes et nombres transcendants (Colloque de Luminy, 1982) (Progress in Mathematics 31), Birkhäuser (Boston, 1983), 271–287.Google Scholar