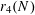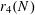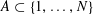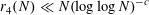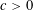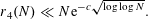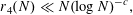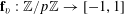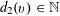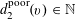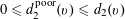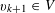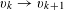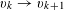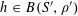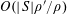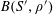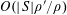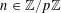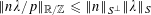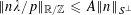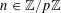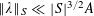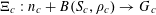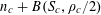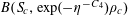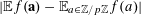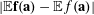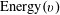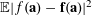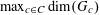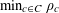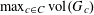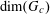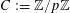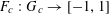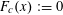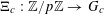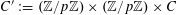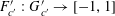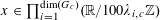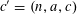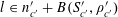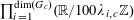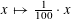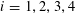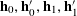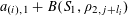1 Introduction
Let
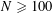 $N\geqslant 100$
be a natural number (so that
$N\geqslant 100$
be a natural number (so that
 $\log \log N$
is positive). If
$\log \log N$
is positive). If
![]() $k\geqslant 3$
is a natural number we define
$k\geqslant 3$
is a natural number we define
![]() $r_{k}(N)$
to be the largest cardinality of a set
$r_{k}(N)$
to be the largest cardinality of a set
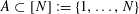 $A\subset [N]:=\{1,\ldots ,N\}$
that does not contain an arithmetic progression of
$A\subset [N]:=\{1,\ldots ,N\}$
that does not contain an arithmetic progression of
![]() $k$
distinct elements.
$k$
distinct elements.
Klaus Roth proved in 1953 [Reference Roth24] that
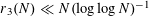 $r_{3}(N)\ll N(\log \log N)^{-1}$
, and so in particularFootnote
1
$r_{3}(N)\ll N(\log \log N)^{-1}$
, and so in particularFootnote
1
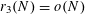 $r_{3}(N)=o(N)$
as
$r_{3}(N)=o(N)$
as
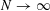 $N\rightarrow \infty$
. Since Szemerédi’s 1969 proof [Reference Szemerédi29] that
$N\rightarrow \infty$
. Since Szemerédi’s 1969 proof [Reference Szemerédi29] that
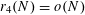 $r_{4}(N)=o(N)$
, and his later proof [Reference Szemerédi30] that
$r_{4}(N)=o(N)$
, and his later proof [Reference Szemerédi30] that
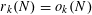 $r_{k}(N)=o_{k}(N)$
for
$r_{k}(N)=o_{k}(N)$
for
![]() $k\geqslant 5$
(answering a question from [Reference Erdős and Turán10]), it has been natural to ask for similarly effective bounds for these quantities. It is worth noting that the famous conjecture of Erdős [Reference Erdős9] asserting that every set of natural numbers whose sum of reciprocals is divergent is equivalent to the claim that
$k\geqslant 5$
(answering a question from [Reference Erdős and Turán10]), it has been natural to ask for similarly effective bounds for these quantities. It is worth noting that the famous conjecture of Erdős [Reference Erdős9] asserting that every set of natural numbers whose sum of reciprocals is divergent is equivalent to the claim that
 $\sum _{n=1}^{\infty }r_{k}(2^{n})/2^{n}<\infty$
for all
$\sum _{n=1}^{\infty }r_{k}(2^{n})/2^{n}<\infty$
for all
![]() $k\geqslant 3$
(see [Reference Tao and Vu33, Exercise 10.0.6]).
$k\geqslant 3$
(see [Reference Tao and Vu33, Exercise 10.0.6]).
A first attempt towards quantitative bounds for higher
![]() $k$
was made by Roth in [Reference Roth25], who provided a new proof that
$k$
was made by Roth in [Reference Roth25], who provided a new proof that
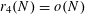 $r_{4}(N)=o(N)$
. A major breakthrough was made in 1998 by Gowers [Reference Gowers11, Reference Gowers12], who obtained the bound
$r_{4}(N)=o(N)$
. A major breakthrough was made in 1998 by Gowers [Reference Gowers11, Reference Gowers12], who obtained the bound
 $r_{k}(N)\ll _{k}N(\log \log N)^{-\unicode[STIX]{x1D716}_{k}}$
for each
$r_{k}(N)\ll _{k}N(\log \log N)^{-\unicode[STIX]{x1D716}_{k}}$
for each
![]() $k\geqslant 4$
, where
$k\geqslant 4$
, where
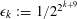 $\unicode[STIX]{x1D716}_{k}:=1/2^{2^{k+9}}$
. In the other direction, a classical result of Behrend [Reference Behrend2] shows that
$\unicode[STIX]{x1D716}_{k}:=1/2^{2^{k+9}}$
. In the other direction, a classical result of Behrend [Reference Behrend2] shows that
 $r_{3}(N)\gg N\exp (-c\sqrt{\log N})$
for some absolute constant
$r_{3}(N)\gg N\exp (-c\sqrt{\log N})$
for some absolute constant
![]() $c>0$
(see [Reference Elkin8, Reference Green and Wolf20] for a slight refinement of this bound), and in [Reference Rankin23] (see also [Reference Łaba and Lacey22]) the argument was generalized to give the bound
$c>0$
(see [Reference Elkin8, Reference Green and Wolf20] for a slight refinement of this bound), and in [Reference Rankin23] (see also [Reference Łaba and Lacey22]) the argument was generalized to give the bound
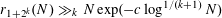 $r_{1+2^{k}}(N)\gg _{k}N\exp (-c\log ^{1/(k+1)}N)$
for any
$r_{1+2^{k}}(N)\gg _{k}N\exp (-c\log ^{1/(k+1)}N)$
for any
![]() $k\geqslant 1$
.
$k\geqslant 1$
.
In the meantime, there has been progress on
![]() $r_{3}(N)$
. Szemerédi (unpublished) obtained the bound
$r_{3}(N)$
. Szemerédi (unpublished) obtained the bound
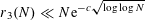 $r_{3}(N)\ll N\text{e}^{-c\sqrt{\log \log N}}$
, and shortly thereafter Heath-Brown [Reference Heath-Brown21] and Szemerédi [Reference Szemerédi32] independently obtained the bound
$r_{3}(N)\ll N\text{e}^{-c\sqrt{\log \log N}}$
, and shortly thereafter Heath-Brown [Reference Heath-Brown21] and Szemerédi [Reference Szemerédi32] independently obtained the bound
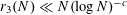 $r_{3}(N)\ll N(\log N)^{-c}$
for some absolute constant
$r_{3}(N)\ll N(\log N)^{-c}$
for some absolute constant
![]() $c>0$
. The best known value of
$c>0$
. The best known value of
![]() $c$
has been improved in a series of papers [Reference Bloom4, Reference Bourgain6, Reference Bourgain7, Reference Sanders27, Reference Sanders28]. Sanders [Reference Sanders28] was the first to show that any
$c$
has been improved in a series of papers [Reference Bloom4, Reference Bourgain6, Reference Bourgain7, Reference Sanders27, Reference Sanders28]. Sanders [Reference Sanders28] was the first to show that any
![]() $c<1$
is admissible, and Bloom [Reference Bloom4] improved the factor of
$c<1$
is admissible, and Bloom [Reference Bloom4] improved the factor of
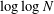 $\log \log N$
in Sanders’s bound.
$\log \log N$
in Sanders’s bound.
The only other direct progress on upper bounds for
![]() $r_{k}(N)$
is our previous paper [Reference Green, Tao, Chen, Gowers, Halberstam, Schmidt and Vaughan19], obtaining the bound
$r_{k}(N)$
is our previous paper [Reference Green, Tao, Chen, Gowers, Halberstam, Schmidt and Vaughan19], obtaining the bound
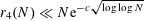 $r_{4}(N)\ll N\text{e}^{-c\sqrt{\log \log N}}$
. The main objective of this paper is to obtain a bound for
$r_{4}(N)\ll N\text{e}^{-c\sqrt{\log \log N}}$
. The main objective of this paper is to obtain a bound for
![]() $r_{4}(N)$
of the same quality as the Heath-Brown and Szemerédi bound for
$r_{4}(N)$
of the same quality as the Heath-Brown and Szemerédi bound for
![]() $r_{3}(N)$
.
$r_{3}(N)$
.
Theorem 1.1. We have
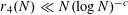 $r_{4}(N)\ll N(\log N)^{-c}$
for some absolute constant
$r_{4}(N)\ll N(\log N)^{-c}$
for some absolute constant
![]() $c>0$
.
$c>0$
.
An analogous result in finite fields was claimed (and published [Reference Green and Tao15]) by us around 12 years ago, although an error in this paper came to light some years later. This was corrected around 5 years ago in [Reference Green and Tao16]. These papers (like almost all of the previously cited quantitative results on
![]() $r_{k}(N)$
) are based on the density increment argument of Roth [Reference Roth24]. However we will use a slightly different “energy decrement” and “regularity” approach here, inspired by the Khinchin-type recurrence theorems for length-four progressions established by Bergelson et al [Reference Bergelson, Host and Kra3] in the ergodic setting, and by the authors [Reference Green13] in the combinatorial setting.
$r_{k}(N)$
) are based on the density increment argument of Roth [Reference Roth24]. However we will use a slightly different “energy decrement” and “regularity” approach here, inspired by the Khinchin-type recurrence theorems for length-four progressions established by Bergelson et al [Reference Bergelson, Host and Kra3] in the ergodic setting, and by the authors [Reference Green13] in the combinatorial setting.
2 Notation
We use the asymptotic notation
![]() $X\ll Y$
or
$X\ll Y$
or
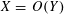 $X=O(Y)$
to denote
$X=O(Y)$
to denote
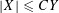 $|X|\leqslant CY$
for some constant
$|X|\leqslant CY$
for some constant
![]() $C$
. Given an asymptotic parameter
$C$
. Given an asymptotic parameter
![]() $N$
going to infinity, we use
$N$
going to infinity, we use
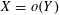 $X=o(Y)$
to denote the bound
$X=o(Y)$
to denote the bound
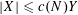 $|X|\leqslant c(N)Y$
for some function
$|X|\leqslant c(N)Y$
for some function
![]() $c(N)$
of
$c(N)$
of
![]() $N$
that goes to zero as
$N$
that goes to zero as
![]() $N$
goes to infinity. We also write
$N$
goes to infinity. We also write
![]() $X\asymp Y$
for
$X\asymp Y$
for
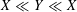 $X\ll Y\ll X$
. If we need the implied constant
$X\ll Y\ll X$
. If we need the implied constant
![]() $C$
or decay function
$C$
or decay function
![]() $c(\,)$
to depend on an additional parameter, we indicate this by subscripts, e.g.
$c(\,)$
to depend on an additional parameter, we indicate this by subscripts, e.g.
 $X=o_{k}(Y)$
denotes the bound
$X=o_{k}(Y)$
denotes the bound
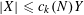 $|X|\leqslant c_{k}(N)Y$
for a function
$|X|\leqslant c_{k}(N)Y$
for a function
![]() $c_{k}(N)$
that goes to zero as
$c_{k}(N)$
that goes to zero as
 $N\rightarrow \infty$
for any fixed choice of
$N\rightarrow \infty$
for any fixed choice of
![]() $k$
.
$k$
.
We will frequently use probabilistic notation, and adopt the convention that boldface variables such as
![]() $\mathbf{a}$
or
$\mathbf{a}$
or
![]() $\mathbf{r}$
represent random variables, whereas non-boldface variables such as
$\mathbf{r}$
represent random variables, whereas non-boldface variables such as
![]() $a$
and
$a$
and
![]() $r$
represent deterministic variables (or constants). We write
$r$
represent deterministic variables (or constants). We write
![]() $\mathbb{P}(E)$
for the probability of a random event
$\mathbb{P}(E)$
for the probability of a random event
![]() $E$
, and
$E$
, and
![]() $\mathbb{E}\mathbf{X}$
and
$\mathbb{E}\mathbf{X}$
and
![]() $\operatorname{Var}\mathbf{X}$
for the expectation and variance of a real or complex random variable
$\operatorname{Var}\mathbf{X}$
for the expectation and variance of a real or complex random variable
![]() $\mathbf{X}$
; we also use
$\mathbf{X}$
; we also use
 $\mathbb{E}(\mathbf{X}|E)=\mathbb{E}\mathbf{X}1_{E}/\mathbb{P}(E)$
for the conditional expectation of
$\mathbb{E}(\mathbf{X}|E)=\mathbb{E}\mathbf{X}1_{E}/\mathbb{P}(E)$
for the conditional expectation of
![]() $\mathbf{X}$
relative to an event
$\mathbf{X}$
relative to an event
![]() $E$
of non-zero probability, where of course
$E$
of non-zero probability, where of course
![]() $1_{E}$
denotes the indicator variable of
$1_{E}$
denotes the indicator variable of
![]() $E$
. In this paper, the random variables
$E$
. In this paper, the random variables
![]() $\mathbf{X}$
of which we will compute expectations of will be discrete, in the sense that they take only finitely many values, so there will be no issues of measurability. The essential range of a discrete random variable
$\mathbf{X}$
of which we will compute expectations of will be discrete, in the sense that they take only finitely many values, so there will be no issues of measurability. The essential range of a discrete random variable
![]() $\mathbf{X}$
is the set of all values
$\mathbf{X}$
is the set of all values
![]() $X$
for which
$X$
for which
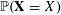 $\mathbb{P}(\mathbf{X}=X)$
is non-zero.
$\mathbb{P}(\mathbf{X}=X)$
is non-zero.
By a slight abuse of notation, we also retain the traditional (in additive combinatorics) use for
![]() $\mathbb{E}$
as an average, thus
$\mathbb{E}$
as an average, thus
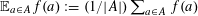 $\mathbb{E}_{a\in A}f(a):=(1/|A|)\sum _{a\in A}f(a)$
for any finite non-empty set
$\mathbb{E}_{a\in A}f(a):=(1/|A|)\sum _{a\in A}f(a)$
for any finite non-empty set
![]() $A$
and function
$A$
and function
 $f:A\rightarrow \mathbb{C}$
, where we use
$f:A\rightarrow \mathbb{C}$
, where we use
![]() $|A|$
to denote the cardinality of
$|A|$
to denote the cardinality of
![]() $A$
. Thus for instance
$A$
. Thus for instance
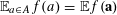 $\mathbb{E}_{a\in A}f(a)=\mathbb{E}f(\mathbf{a})$
if
$\mathbb{E}_{a\in A}f(a)=\mathbb{E}f(\mathbf{a})$
if
![]() $\mathbf{a}$
is drawn uniformly at random from
$\mathbf{a}$
is drawn uniformly at random from
![]() $A$
.
$A$
.
A function
 $f:A\rightarrow \mathbb{C}$
is said to be
$f:A\rightarrow \mathbb{C}$
is said to be
![]() $1$
-bounded if one has
$1$
-bounded if one has
 $|f(a)|\leqslant 1$
for all
$|f(a)|\leqslant 1$
for all
![]() $a\in A$
. We will frequently rely on the following probabilistic form of the Cauchy–Schwarz inequality, the proof of which is an exercise.
$a\in A$
. We will frequently rely on the following probabilistic form of the Cauchy–Schwarz inequality, the proof of which is an exercise.
Lemma 2.1 (Cauchy–Schwarz).
Let
![]() $A,B$
be sets, let
$A,B$
be sets, let
 $f:A\rightarrow \mathbb{C}$
be a
$f:A\rightarrow \mathbb{C}$
be a
![]() $1$
-bounded function, and let
$1$
-bounded function, and let
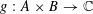 $g:A\times B\rightarrow \mathbb{C}$
be another function. Let
$g:A\times B\rightarrow \mathbb{C}$
be another function. Let
![]() $\mathbf{a},\mathbf{b},\mathbf{b}^{\prime }$
be discrete random variables in
$\mathbf{a},\mathbf{b},\mathbf{b}^{\prime }$
be discrete random variables in
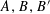 $A,B,B^{\prime }$
respectively, such that
$A,B,B^{\prime }$
respectively, such that
![]() $\mathbf{b}^{\prime }$
is a conditionally independent copy of
$\mathbf{b}^{\prime }$
is a conditionally independent copy of
![]() $\mathbf{b}$
relative to
$\mathbf{b}$
relative to
![]() $\mathbf{a}$
, that is to say that
$\mathbf{a}$
, that is to say that
 $$\begin{eqnarray}\mathbb{P}(\mathbf{b}=b,\mathbf{b}^{\prime }=b^{\prime }|\mathbf{a}=a)=\mathbb{P}(\mathbf{b}=b|\mathbf{a}=a)\mathbb{P}(\mathbf{b}=b^{\prime }|\mathbf{a}=a)\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{b}=b,\mathbf{b}^{\prime }=b^{\prime }|\mathbf{a}=a)=\mathbb{P}(\mathbf{b}=b|\mathbf{a}=a)\mathbb{P}(\mathbf{b}=b^{\prime }|\mathbf{a}=a)\end{eqnarray}$$
for all
![]() $a$
in the essential range of
$a$
in the essential range of
![]() $\mathbf{a}$
and all
$\mathbf{a}$
and all
 $b,b^{\prime }\in B$
. Then we have
$b,b^{\prime }\in B$
. Then we have
 $$\begin{eqnarray}|\mathbb{E}f(\mathbf{a})g(\mathbf{a},\mathbf{b})|^{2}\leqslant \mathbb{E}g(\mathbf{a},\mathbf{b})\overline{g(\mathbf{a},\mathbf{b}^{\prime })}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f(\mathbf{a})g(\mathbf{a},\mathbf{b})|^{2}\leqslant \mathbb{E}g(\mathbf{a},\mathbf{b})\overline{g(\mathbf{a},\mathbf{b}^{\prime })}.\end{eqnarray}$$
We will think of this lemma as allowing one to eliminate a factor
![]() $f(\mathbf{a})$
from a lower bound of the form
$f(\mathbf{a})$
from a lower bound of the form
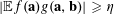 $|\mathbb{E}f(\mathbf{a})g(\mathbf{a},\mathbf{b})|\geqslant \unicode[STIX]{x1D702}$
, at the cost of duplicating the factor
$|\mathbb{E}f(\mathbf{a})g(\mathbf{a},\mathbf{b})|\geqslant \unicode[STIX]{x1D702}$
, at the cost of duplicating the factor
![]() $g$
, and worsening the lower bound from
$g$
, and worsening the lower bound from
![]() $\unicode[STIX]{x1D702}$
to
$\unicode[STIX]{x1D702}$
to
![]() $\unicode[STIX]{x1D702}^{2}$
.
$\unicode[STIX]{x1D702}^{2}$
.
We also have the following variant of Lemma 2.1.
Lemma 2.2 (Popularity principle).
Let
![]() $\mathbf{a}$
be a random variable taking values in a set
$\mathbf{a}$
be a random variable taking values in a set
![]() $A$
, and let
$A$
, and let
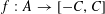 $f:A\rightarrow [-C,C]$
be a function for some
$f:A\rightarrow [-C,C]$
be a function for some
![]() $C>0$
. If we have
$C>0$
. If we have
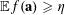 $\mathbb{E}f(\mathbf{a})\geqslant \unicode[STIX]{x1D702}$
for some
$\mathbb{E}f(\mathbf{a})\geqslant \unicode[STIX]{x1D702}$
for some
![]() $\unicode[STIX]{x1D702}>0$
then, with probability at least
$\unicode[STIX]{x1D702}>0$
then, with probability at least
![]() $\unicode[STIX]{x1D702}/2C$
, the random variable
$\unicode[STIX]{x1D702}/2C$
, the random variable
![]() $\mathbf{a}$
attains a value
$\mathbf{a}$
attains a value
![]() $a\in A$
for which
$a\in A$
for which
 $f(a)\geqslant \unicode[STIX]{x1D702}/2$
.
$f(a)\geqslant \unicode[STIX]{x1D702}/2$
.
Proof. If we set
 $\unicode[STIX]{x1D6FA}:=\{a\in A:f(a)\geqslant \unicode[STIX]{x1D702}/2\}$
, then
$\unicode[STIX]{x1D6FA}:=\{a\in A:f(a)\geqslant \unicode[STIX]{x1D702}/2\}$
, then
 $$\begin{eqnarray}f(\mathbf{a})\leqslant \frac{\unicode[STIX]{x1D702}}{2}+C1_{\mathbf{a}\in \unicode[STIX]{x1D6FA}}\end{eqnarray}$$
$$\begin{eqnarray}f(\mathbf{a})\leqslant \frac{\unicode[STIX]{x1D702}}{2}+C1_{\mathbf{a}\in \unicode[STIX]{x1D6FA}}\end{eqnarray}$$
and hence on taking expectations
 $$\begin{eqnarray}\mathbb{E}f(\mathbf{a})\leqslant \frac{\unicode[STIX]{x1D702}}{2}+C\mathbb{P}(\mathbf{a}\in \unicode[STIX]{x1D6FA}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f(\mathbf{a})\leqslant \frac{\unicode[STIX]{x1D702}}{2}+C\mathbb{P}(\mathbf{a}\in \unicode[STIX]{x1D6FA}).\end{eqnarray}$$
This implies that
 $$\begin{eqnarray}\mathbb{P}(\mathbf{a}\in \unicode[STIX]{x1D6FA})\geqslant \unicode[STIX]{x1D702}/2C\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{a}\in \unicode[STIX]{x1D6FA})\geqslant \unicode[STIX]{x1D702}/2C\end{eqnarray}$$
giving the claim. ◻
If
![]() $\unicode[STIX]{x1D703}\in \mathbb{R}$
, we write
$\unicode[STIX]{x1D703}\in \mathbb{R}$
, we write
![]() $\Vert \unicode[STIX]{x1D703}\Vert _{\mathbb{R}/\mathbb{Z}}$
for the distance from
$\Vert \unicode[STIX]{x1D703}\Vert _{\mathbb{R}/\mathbb{Z}}$
for the distance from
![]() $\unicode[STIX]{x1D703}$
to the nearest integer, and
$\unicode[STIX]{x1D703}$
to the nearest integer, and
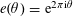 $e(\unicode[STIX]{x1D703})=\text{e}^{2\unicode[STIX]{x1D70B}\text{i}\unicode[STIX]{x1D703}}$
. Observe from elementary trigonometry that
$e(\unicode[STIX]{x1D703})=\text{e}^{2\unicode[STIX]{x1D70B}\text{i}\unicode[STIX]{x1D703}}$
. Observe from elementary trigonometry that
 $$\begin{eqnarray}|e(\unicode[STIX]{x1D703})-1|=2|\text{sin}(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703})|\asymp \Vert \unicode[STIX]{x1D703}\Vert _{\mathbb{R}/\mathbb{Z}}\end{eqnarray}$$
$$\begin{eqnarray}|e(\unicode[STIX]{x1D703})-1|=2|\text{sin}(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703})|\asymp \Vert \unicode[STIX]{x1D703}\Vert _{\mathbb{R}/\mathbb{Z}}\end{eqnarray}$$
and hence also
 $$\begin{eqnarray}1-\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703})=2|\text{sin}(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703})|^{2}\asymp \Vert \unicode[STIX]{x1D703}\Vert _{\mathbb{ R}/\mathbb{Z}}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}1-\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703})=2|\text{sin}(\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703})|^{2}\asymp \Vert \unicode[STIX]{x1D703}\Vert _{\mathbb{ R}/\mathbb{Z}}^{2}.\end{eqnarray}$$
We will also use the triangle inequalities
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2}\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant \Vert \unicode[STIX]{x1D703}_{1}\Vert _{\mathbb{R}/\mathbb{Z}}+\Vert \unicode[STIX]{x1D703}_{2}\Vert _{\mathbb{R}/\mathbb{Z}};\qquad \Vert k\unicode[STIX]{x1D703}\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant |k|\Vert \unicode[STIX]{x1D703}\Vert _{\mathbb{R}/\mathbb{Z}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2}\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant \Vert \unicode[STIX]{x1D703}_{1}\Vert _{\mathbb{R}/\mathbb{Z}}+\Vert \unicode[STIX]{x1D703}_{2}\Vert _{\mathbb{R}/\mathbb{Z}};\qquad \Vert k\unicode[STIX]{x1D703}\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant |k|\Vert \unicode[STIX]{x1D703}\Vert _{\mathbb{R}/\mathbb{Z}}\end{eqnarray}$$
for
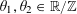 $\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2}\in \mathbb{R}/\mathbb{Z}$
and
$\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2}\in \mathbb{R}/\mathbb{Z}$
and
![]() $k\in \mathbb{Z}$
frequently in the sequel, often without further comment.
$k\in \mathbb{Z}$
frequently in the sequel, often without further comment.
For any prime
![]() $p$
, we (by slight abuse of notation) let
$p$
, we (by slight abuse of notation) let
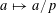 $a\mapsto a/p$
be the obvious homomorphism from
$a\mapsto a/p$
be the obvious homomorphism from
![]() $\mathbb{Z}/p\mathbb{Z}$
to
$\mathbb{Z}/p\mathbb{Z}$
to
![]() $\mathbb{R}/\mathbb{Z}$
that maps
$\mathbb{R}/\mathbb{Z}$
that maps
 $a~(\operatorname{mod}~p)$
to
$a~(\operatorname{mod}~p)$
to
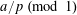 $a/p~(\operatorname{mod}~1)$
for any integer
$a/p~(\operatorname{mod}~1)$
for any integer
![]() $a$
. We then define
$a$
. We then define
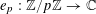 $e_{p}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
to be the character
$e_{p}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
to be the character
 $$\begin{eqnarray}e_{p}(a):=e\biggl(\frac{a}{p}\biggr)=\text{e}^{2\unicode[STIX]{x1D70B}\text{i}a/p}\end{eqnarray}$$
$$\begin{eqnarray}e_{p}(a):=e\biggl(\frac{a}{p}\biggr)=\text{e}^{2\unicode[STIX]{x1D70B}\text{i}a/p}\end{eqnarray}$$
of
![]() $\mathbb{Z}/p\mathbb{Z}$
.
$\mathbb{Z}/p\mathbb{Z}$
.
3 High-level overview of argument
We will establish Theorem 1.1 by establishing the following result, related to the Khinchin-type recurrence theorems mentioned earlier. It will be convenient to introduce the notation
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}):=\mathbb{E}\mathbf{f}(\mathbf{a})\mathbf{f}(\mathbf{a}+\mathbf{r})\mathbf{f}(\mathbf{a}+2\mathbf{r})\mathbf{f}(\mathbf{a}+3\mathbf{r})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}):=\mathbb{E}\mathbf{f}(\mathbf{a})\mathbf{f}(\mathbf{a}+\mathbf{r})\mathbf{f}(\mathbf{a}+2\mathbf{r})\mathbf{f}(\mathbf{a}+3\mathbf{r})\end{eqnarray}$$
whenever
![]() $\mathbf{a},\mathbf{r}$
are random variables on
$\mathbf{a},\mathbf{r}$
are random variables on
![]() $\mathbb{Z}/p\mathbb{Z}$
and
$\mathbb{Z}/p\mathbb{Z}$
and
 $\mathbf{f}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
is a random function; of course, the notation can also be applied to deterministic functions
$\mathbf{f}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
is a random function; of course, the notation can also be applied to deterministic functions
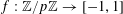 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
. Later on we will also need the conditional variant
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
. Later on we will also need the conditional variant
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}|E):=\mathbb{E}(\mathbf{f}(\mathbf{a})\mathbf{f}(\mathbf{a}+\mathbf{r})\mathbf{f}(\mathbf{a}+2\mathbf{r})\mathbf{f}(\mathbf{a}+3\mathbf{r})|E)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}|E):=\mathbb{E}(\mathbf{f}(\mathbf{a})\mathbf{f}(\mathbf{a}+\mathbf{r})\mathbf{f}(\mathbf{a}+2\mathbf{r})\mathbf{f}(\mathbf{a}+3\mathbf{r})|E)\end{eqnarray}$$
for some events
![]() $E$
of non-zero probability. Informally, this quantity counts the density of arithmetic progressions
$E$
of non-zero probability. Informally, this quantity counts the density of arithmetic progressions
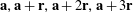 $\mathbf{a},\mathbf{a}\,+\,\mathbf{r},\mathbf{a}\,+\,2\mathbf{r},\mathbf{a}\,+\,3\mathbf{r}$
on the event
$\mathbf{a},\mathbf{a}\,+\,\mathbf{r},\mathbf{a}\,+\,2\mathbf{r},\mathbf{a}\,+\,3\mathbf{r}$
on the event
![]() $E$
weighted by
$E$
weighted by
![]() $\mathbf{f}$
, where
$\mathbf{f}$
, where
![]() $\mathbf{a},\mathbf{r}$
need not be drawn uniformly or independently (and
$\mathbf{a},\mathbf{r}$
need not be drawn uniformly or independently (and
![]() $\mathbf{f}$
may also be coupled to
$\mathbf{f}$
may also be coupled to
![]() $\mathbf{a},\mathbf{r}$
).
$\mathbf{a},\mathbf{r}$
).
Theorem 3.1. Let
![]() $p$
be a prime, let
$p$
be a prime, let
![]() $\unicode[STIX]{x1D702}$
be a real number with
$\unicode[STIX]{x1D702}$
be a real number with
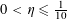 $0<\unicode[STIX]{x1D702}\leqslant {\textstyle \frac{1}{10}}$
, and let
$0<\unicode[STIX]{x1D702}\leqslant {\textstyle \frac{1}{10}}$
, and let
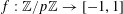 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
be a function. Then there exist random variables
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
be a function. Then there exist random variables
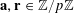 $\mathbf{a},\mathbf{r}\in \mathbb{Z}/p\mathbb{Z}$
, not necessarily independent, obeying the near-uniform distribution bound
$\mathbf{a},\mathbf{r}\in \mathbb{Z}/p\mathbb{Z}$
, not necessarily independent, obeying the near-uniform distribution bound
 $$\begin{eqnarray}\mathbb{E}f(\mathbf{a})=\mathbb{E}_{x\in \mathbb{Z}/p\mathbb{Z}}f(x)+O(\unicode[STIX]{x1D702}),\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f(\mathbf{a})=\mathbb{E}_{x\in \mathbb{Z}/p\mathbb{Z}}f(x)+O(\unicode[STIX]{x1D702}),\end{eqnarray}$$
the recurrence property
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f)\geqslant (\mathbb{E}f(\mathbf{a}))^{4}-O(\unicode[STIX]{x1D702}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f)\geqslant (\mathbb{E}f(\mathbf{a}))^{4}-O(\unicode[STIX]{x1D702}),\end{eqnarray}$$
and the “thickness” bound
 $$\begin{eqnarray}\mathbb{P}(\mathbf{r}=0)\ll \exp (-\unicode[STIX]{x1D702}^{-O(1)})/p.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{r}=0)\ll \exp (-\unicode[STIX]{x1D702}^{-O(1)})/p.\end{eqnarray}$$
We note that a variant of Theorem 3.1 was established by us in [Reference Green13] (answering a question in [Reference Bergelson, Host and Kra3]), in which the random variable
![]() $\mathbf{a}$
was uniformly distributed in
$\mathbf{a}$
was uniformly distributed in
![]() $\mathbb{Z}/p\mathbb{Z}$
, the random variable
$\mathbb{Z}/p\mathbb{Z}$
, the random variable
![]() $\mathbf{r}$
was uniformly distributed in a subset of
$\mathbf{r}$
was uniformly distributed in a subset of
![]() $\mathbb{Z}/p\mathbb{Z}$
of size
$\mathbb{Z}/p\mathbb{Z}$
of size
![]() $\gg _{\unicode[STIX]{x1D702}}p$
and was independent of
$\gg _{\unicode[STIX]{x1D702}}p$
and was independent of
![]() $\mathbf{a}$
, and the condition (3.4) (which is crucial to the quantitative bound in Theorem 1.1) was not present. Compared to that result, Theorem 3.1 obtains the much more quantitative bound (3.4), but at the expense of no longer enforcing independence between
$\mathbf{a}$
, and the condition (3.4) (which is crucial to the quantitative bound in Theorem 1.1) was not present. Compared to that result, Theorem 3.1 obtains the much more quantitative bound (3.4), but at the expense of no longer enforcing independence between
![]() $\mathbf{a}$
and
$\mathbf{a}$
and
![]() $\mathbf{r}$
. The use of non-independent random variables
$\mathbf{r}$
. The use of non-independent random variables
![]() $\mathbf{a},\mathbf{r}$
is an innovation of this current paper; it is similar to the technique in previous papers of using “factors” (finite partitions) to break up the domain
$\mathbf{a},\mathbf{r}$
is an innovation of this current paper; it is similar to the technique in previous papers of using “factors” (finite partitions) to break up the domain
![]() $\mathbb{Z}/p\mathbb{Z}$
into smaller “atoms” such as Bohr sets and analyzing each atom separately. However there will be technical advantages from the more general framework of pairs of independent random variables
$\mathbb{Z}/p\mathbb{Z}$
into smaller “atoms” such as Bohr sets and analyzing each atom separately. However there will be technical advantages from the more general framework of pairs of independent random variables
![]() $\mathbf{a},\mathbf{r}$
. In particular we will be able to avoid some of the boundary issues arising from irregularity of Bohr sets, by using the smoother device of “regular probability distributions” associated to such sets. Although
$\mathbf{a},\mathbf{r}$
. In particular we will be able to avoid some of the boundary issues arising from irregularity of Bohr sets, by using the smoother device of “regular probability distributions” associated to such sets. Although
![]() $f$
is allowed to attain negative values in Theorem 3.1, in our applications we shall only be concerned with the case when
$f$
is allowed to attain negative values in Theorem 3.1, in our applications we shall only be concerned with the case when
![]() $f$
is non-negative.
$f$
is non-negative.
Let us now see how Theorem 1.1 follows from Theorem 3.1. Clearly we may assume that
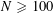 $N\geqslant 100$
. Suppose that
$N\geqslant 100$
. Suppose that
![]() $A$
is a subset of
$A$
is a subset of
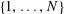 $\{1,\ldots ,N\}$
without any non-trivial four-term arithmetic progressions. By Bertrand’s postulate, we may find a prime
$\{1,\ldots ,N\}$
without any non-trivial four-term arithmetic progressions. By Bertrand’s postulate, we may find a prime
![]() $p$
between (for example)
$p$
between (for example)
![]() $2N$
and
$2N$
and
![]() $4N$
. If we define
$4N$
. If we define
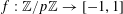 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
to be the indicator function
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
to be the indicator function
![]() $1_{A}$
of
$1_{A}$
of
![]() $A$
(viewed as a subset of
$A$
(viewed as a subset of
![]() $\mathbb{Z}/p\mathbb{Z}$
), then we have
$\mathbb{Z}/p\mathbb{Z}$
), then we have
 $$\begin{eqnarray}\mathbb{E}_{x\in \mathbb{Z}/p\mathbb{Z}}f(x)=\frac{|A|}{p}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{x\in \mathbb{Z}/p\mathbb{Z}}f(x)=\frac{|A|}{p}\end{eqnarray}$$
and also
 $$\begin{eqnarray}f(a)f(a+r)f(a+2r)f(a+3r)=0\end{eqnarray}$$
$$\begin{eqnarray}f(a)f(a+r)f(a+2r)f(a+3r)=0\end{eqnarray}$$
whenever
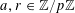 $a,r\in \mathbb{Z}/p\mathbb{Z}$
with
$a,r\in \mathbb{Z}/p\mathbb{Z}$
with
![]() $r$
non-zero. Now let
$r$
non-zero. Now let
![]() $\mathbf{a},\mathbf{r}$
be as in Theorem 3.1, with
$\mathbf{a},\mathbf{r}$
be as in Theorem 3.1, with
![]() $\unicode[STIX]{x1D702}$
to be chosen later. From (3.2), (3.3), (3.5) we have
$\unicode[STIX]{x1D702}$
to be chosen later. From (3.2), (3.3), (3.5) we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f)\geqslant \biggl(\frac{|A|}{p}\biggr)^{4}-O(\unicode[STIX]{x1D702}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f)\geqslant \biggl(\frac{|A|}{p}\biggr)^{4}-O(\unicode[STIX]{x1D702}).\end{eqnarray}$$
But by (3.6), (3.4), the left-hand side is
 $O(\exp (-\unicode[STIX]{x1D702}^{-O(1)})/p)$
. Setting
$O(\exp (-\unicode[STIX]{x1D702}^{-O(1)})/p)$
. Setting
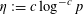 $\unicode[STIX]{x1D702}:=c\log ^{-c}p$
for a sufficiently small absolute constant
$\unicode[STIX]{x1D702}:=c\log ^{-c}p$
for a sufficiently small absolute constant
![]() $c>0$
, we conclude that
$c>0$
, we conclude that
 $$\begin{eqnarray}\biggl(\frac{|A|}{p}\biggr)^{4}\ll \log ^{-c}p\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\frac{|A|}{p}\biggr)^{4}\ll \log ^{-c}p\end{eqnarray}$$
and hence
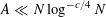 $A\ll N\log ^{-c/4}N$
, giving Theorem 1.1.
$A\ll N\log ^{-c/4}N$
, giving Theorem 1.1.
Remark.
As mentioned previously, the arguments in [Reference Green13] established a bound of the form (3.3) with
![]() $\mathbf{a}$
and
$\mathbf{a}$
and
![]() $\mathbf{r}$
independent, and also one could ensure that
$\mathbf{r}$
independent, and also one could ensure that
![]() $\mathbf{a}$
was uniformly distributed over
$\mathbf{a}$
was uniformly distributed over
![]() $\mathbb{Z}/p\mathbb{Z}$
. As a consequence, one could establish a variant of Theorem 1.1, namely that for any
$\mathbb{Z}/p\mathbb{Z}$
. As a consequence, one could establish a variant of Theorem 1.1, namely that for any
![]() $N\geqslant 1$
,
$N\geqslant 1$
,
![]() $\unicode[STIX]{x1D702}>0$
, and
$\unicode[STIX]{x1D702}>0$
, and
 $A\subset [N]$
, one had
$A\subset [N]$
, one had
 $$\begin{eqnarray}\frac{|A\cap (A-r)\cap (A-2r)\cap (A-3r)|}{N}\geqslant \biggl(\frac{|A|}{N}\biggr)^{4}-\unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}\frac{|A\cap (A-r)\cap (A-2r)\cap (A-3r)|}{N}\geqslant \biggl(\frac{|A|}{N}\biggr)^{4}-\unicode[STIX]{x1D702}\end{eqnarray}$$
for
![]() $\gg _{\unicode[STIX]{x1D702}}N$
choices of
$\gg _{\unicode[STIX]{x1D702}}N$
choices of
 $0\leqslant r\leqslant N$
. Unfortunately our methods do not seem to provide a good bound of this form due to our coupling together of
$0\leqslant r\leqslant N$
. Unfortunately our methods do not seem to provide a good bound of this form due to our coupling together of
![]() $\mathbf{a}$
and
$\mathbf{a}$
and
![]() $\mathbf{r}$
.
$\mathbf{r}$
.
It remains to establish Theorem 3.1. As in [Reference Bergelson, Host and Kra3, Reference Green13], the lower bound (3.3) will ultimately come from the following consequence of the Cauchy–Schwarz inequality that counts solutions to the equation
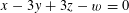 $x-3y+3z-w=0$
for
$x-3y+3z-w=0$
for
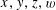 $x,y,z,w$
in some subset of a compact abelian group; this inequality is a specific feature of the theory of length-four progressions that is not available for longer progressionsFootnote
2
.
$x,y,z,w$
in some subset of a compact abelian group; this inequality is a specific feature of the theory of length-four progressions that is not available for longer progressionsFootnote
2
.
Lemma 3.2 (Application of Cauchy–Schwarz).
Let
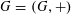 $G=(G,+)$
be a compact abelian group, let
$G=(G,+)$
be a compact abelian group, let
![]() $\unicode[STIX]{x1D707}$
be the probability Haar measure on
$\unicode[STIX]{x1D707}$
be the probability Haar measure on
![]() $G$
, and let
$G$
, and let
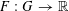 $F:G\rightarrow \mathbb{R}$
be a bounded measurable function. Then
$F:G\rightarrow \mathbb{R}$
be a bounded measurable function. Then
 $$\begin{eqnarray}\int _{G}\int _{G}\int _{G}F(x)F(y)F(z)F(x-3y+3z)\,d\unicode[STIX]{x1D707}(x)\,d\unicode[STIX]{x1D707}(y)\,d\unicode[STIX]{x1D707}(z)\geqslant \biggl(\int _{G}F\,d\unicode[STIX]{x1D707}\biggr)^{4}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{G}\int _{G}\int _{G}F(x)F(y)F(z)F(x-3y+3z)\,d\unicode[STIX]{x1D707}(x)\,d\unicode[STIX]{x1D707}(y)\,d\unicode[STIX]{x1D707}(z)\geqslant \biggl(\int _{G}F\,d\unicode[STIX]{x1D707}\biggr)^{4}.\end{eqnarray}$$
Proof. Making the change of variables
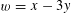 $w=x-3y$
and using Fubini’s theorem, the left-hand side may be rewritten as
$w=x-3y$
and using Fubini’s theorem, the left-hand side may be rewritten as
 $$\begin{eqnarray}\int _{G}\biggl(\int _{G}F(w+3y)F(y)\,d\unicode[STIX]{x1D707}(y)\biggr)^{2}\,d\unicode[STIX]{x1D707}(w),\end{eqnarray}$$
$$\begin{eqnarray}\int _{G}\biggl(\int _{G}F(w+3y)F(y)\,d\unicode[STIX]{x1D707}(y)\biggr)^{2}\,d\unicode[STIX]{x1D707}(w),\end{eqnarray}$$
which by the Cauchy–Schwarz inequality is at least
 $$\begin{eqnarray}\biggl(\int _{G}\int _{G}F(w+3y)F(y)\,d\unicode[STIX]{x1D707}(y)\,d\unicode[STIX]{x1D707}(w)\biggr)^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\int _{G}\int _{G}F(w+3y)F(y)\,d\unicode[STIX]{x1D707}(y)\,d\unicode[STIX]{x1D707}(w)\biggr)^{2}.\end{eqnarray}$$
But by a further application of Fubini’s theorem, the expression inside the square is
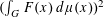 $(\int _{G}F(x)\,d\unicode[STIX]{x1D707}(x))^{2}$
. The claim follows.◻
$(\int _{G}F(x)\,d\unicode[STIX]{x1D707}(x))^{2}$
. The claim follows.◻
To see the relevance of this lemma to Theorem 3.1, and to motivate the strategy of proof of that theorem, let us first test that theorem on some key examples. To simplify the exposition, our discussion will be somewhat non-rigorous in nature; for instance, we will make liberal use of the non-rigorous symbol
![]() ${\approx}$
without quantifying the nature of the approximation.
${\approx}$
without quantifying the nature of the approximation.
Example 1 (A well-distributed pure quadratic factor).
Let
![]() $G$
be the
$G$
be the
![]() $d$
-torus
$d$
-torus
 $G=(\mathbb{R}/\mathbb{Z})^{d}$
for some bounded
$G=(\mathbb{R}/\mathbb{Z})^{d}$
for some bounded
 $d=O(1)$
, and let
$d=O(1)$
, and let
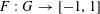 $F:G\rightarrow [-1,1]$
be a smooth function (independent of
$F:G\rightarrow [-1,1]$
be a smooth function (independent of
![]() $p$
); for instance,
$p$
); for instance,
![]() $F$
could be a finite linear combination of characters
$F$
could be a finite linear combination of characters
 $\unicode[STIX]{x1D712}:G\rightarrow S^{1}$
of
$\unicode[STIX]{x1D712}:G\rightarrow S^{1}$
of
![]() $G$
. Let
$G$
. Let
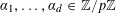 $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{d}\in \mathbb{Z}/p\mathbb{Z}$
be “generic” frequencies, in the sense that there are no non-trivial linear relations of the form
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{d}\in \mathbb{Z}/p\mathbb{Z}$
be “generic” frequencies, in the sense that there are no non-trivial linear relations of the form
 $$\begin{eqnarray}k_{1}\unicode[STIX]{x1D6FC}_{1}+\cdots +k_{d}\unicode[STIX]{x1D6FC}_{d}=0\end{eqnarray}$$
$$\begin{eqnarray}k_{1}\unicode[STIX]{x1D6FC}_{1}+\cdots +k_{d}\unicode[STIX]{x1D6FC}_{d}=0\end{eqnarray}$$
with
 $k_{1},\ldots ,k_{d}=O(1)$
not all equal to zero. We also introduce some additional frequencies
$k_{1},\ldots ,k_{d}=O(1)$
not all equal to zero. We also introduce some additional frequencies
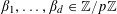 $\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{d}\in \mathbb{Z}/p\mathbb{Z}$
, for which we impose no genericity restrictions. Let
$\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{d}\in \mathbb{Z}/p\mathbb{Z}$
, for which we impose no genericity restrictions. Let
 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
be the function
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
be the function
 $$\begin{eqnarray}f(a):=F(Q(a)),\end{eqnarray}$$
$$\begin{eqnarray}f(a):=F(Q(a)),\end{eqnarray}$$
where
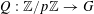 $Q:\mathbb{Z}/p\mathbb{Z}\rightarrow G$
is the quadratic polynomial
$Q:\mathbb{Z}/p\mathbb{Z}\rightarrow G$
is the quadratic polynomial
 $$\begin{eqnarray}Q(a):=\biggl(\frac{\unicode[STIX]{x1D6FC}_{1}a^{2}+\unicode[STIX]{x1D6FD}_{1}a}{p},\ldots ,\frac{\unicode[STIX]{x1D6FC}_{d}a^{2}+\unicode[STIX]{x1D6FD}_{d}a}{p}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}Q(a):=\biggl(\frac{\unicode[STIX]{x1D6FC}_{1}a^{2}+\unicode[STIX]{x1D6FD}_{1}a}{p},\ldots ,\frac{\unicode[STIX]{x1D6FC}_{d}a^{2}+\unicode[STIX]{x1D6FD}_{d}a}{p}\biggr),\end{eqnarray}$$
and where we use the obvious division by zero map
 $a\mapsto a/p$
from
$a\mapsto a/p$
from
![]() $\mathbb{Z}/p\mathbb{Z}$
to
$\mathbb{Z}/p\mathbb{Z}$
to
![]() $\mathbb{R}/\mathbb{Z}$
. For any tuples
$\mathbb{R}/\mathbb{Z}$
. For any tuples
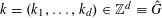 $k=(k_{1},\ldots ,k_{d})\in \mathbb{Z}^{d}\equiv {\hat{G}}$
and
$k=(k_{1},\ldots ,k_{d})\in \mathbb{Z}^{d}\equiv {\hat{G}}$
and
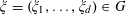 $\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{d})\in G$
, we define the dot product
$\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{d})\in G$
, we define the dot product
 $$\begin{eqnarray}k\cdot \unicode[STIX]{x1D709}:=k_{1}\unicode[STIX]{x1D709}_{1}+\cdots +k_{d}\unicode[STIX]{x1D709}_{d}.\end{eqnarray}$$
$$\begin{eqnarray}k\cdot \unicode[STIX]{x1D709}:=k_{1}\unicode[STIX]{x1D709}_{1}+\cdots +k_{d}\unicode[STIX]{x1D709}_{d}.\end{eqnarray}$$
Because of our genericity hypothesis on the
![]() $\unicode[STIX]{x1D6FC}_{i}$
, we see from Gauss sum estimates that
$\unicode[STIX]{x1D6FC}_{i}$
, we see from Gauss sum estimates that
 $$\begin{eqnarray}\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}e(k\cdot Q(a))\approx 0\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}e(k\cdot Q(a))\approx 0\end{eqnarray}$$
for any bounded tuple
![]() $k\in \mathbb{Z}^{d}$
when
$k\in \mathbb{Z}^{d}$
when
![]() $p$
is large. By the Weyl equidistribution criterion, we thus see that when
$p$
is large. By the Weyl equidistribution criterion, we thus see that when
![]() $p$
is large, the quantity
$p$
is large, the quantity
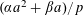 $(\unicode[STIX]{x1D6FC}a^{2}+\unicode[STIX]{x1D6FD}a)/p$
becomes equidistributed in
$(\unicode[STIX]{x1D6FC}a^{2}+\unicode[STIX]{x1D6FD}a)/p$
becomes equidistributed in
![]() $G$
as
$G$
as
![]() $a$
ranges over
$a$
ranges over
![]() $\mathbb{Z}/p\mathbb{Z}$
. In particular, as
$\mathbb{Z}/p\mathbb{Z}$
. In particular, as
![]() $F$
was assumed to be smooth, we expect to have
$F$
was assumed to be smooth, we expect to have
 $$\begin{eqnarray}\mathbb{E}f(\mathbf{a})=\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}f(a)\approx \int _{G}F(x)\,d\unicode[STIX]{x1D707}(x)\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f(\mathbf{a})=\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}f(a)\approx \int _{G}F(x)\,d\unicode[STIX]{x1D707}(x)\end{eqnarray}$$
if
![]() $\mathbf{a}$
is drawn uniformly in
$\mathbf{a}$
is drawn uniformly in
![]() $\mathbb{Z}/p\mathbb{Z}$
. Now suppose that
$\mathbb{Z}/p\mathbb{Z}$
. Now suppose that
![]() $\mathbf{r}$
is also drawn uniformly in
$\mathbf{r}$
is also drawn uniformly in
![]() $\mathbb{Z}/p\mathbb{Z}$
, independently of
$\mathbb{Z}/p\mathbb{Z}$
, independently of
![]() $\mathbf{a}$
. The tuple
$\mathbf{a}$
. The tuple
 $$\begin{eqnarray}(Q(\mathbf{a}),Q(\mathbf{a}+\mathbf{r}),Q(\mathbf{a}+2\mathbf{r}),Q(\mathbf{a}+3\mathbf{r}))\end{eqnarray}$$
$$\begin{eqnarray}(Q(\mathbf{a}),Q(\mathbf{a}+\mathbf{r}),Q(\mathbf{a}+2\mathbf{r}),Q(\mathbf{a}+3\mathbf{r}))\end{eqnarray}$$
will not become equidistributed in
![]() $G^{4}$
, because of the elementary algebraic identity
$G^{4}$
, because of the elementary algebraic identity
 $$\begin{eqnarray}Q(\mathbf{a})-3Q(\mathbf{a}+\mathbf{r})+3Q(\mathbf{a}+2\mathbf{r})-Q(\mathbf{a}+3\mathbf{r})=0,\end{eqnarray}$$
$$\begin{eqnarray}Q(\mathbf{a})-3Q(\mathbf{a}+\mathbf{r})+3Q(\mathbf{a}+2\mathbf{r})-Q(\mathbf{a}+3\mathbf{r})=0,\end{eqnarray}$$
which is a discrete version of the fact that the third derivative of any quadratic polynomial vanishes. However, this turns out to be the only constraint on this tuple in the limit
![]() $p\rightarrow \infty$
. Indeed, from the genericity hypothesis on the
$p\rightarrow \infty$
. Indeed, from the genericity hypothesis on the
![]() $\unicode[STIX]{x1D6FC}_{i}$
, one can verify that the quadratic form
$\unicode[STIX]{x1D6FC}_{i}$
, one can verify that the quadratic form
 $$\begin{eqnarray}(a,r)\mapsto k_{0}\cdot Q_{0}(a)+k_{1}\cdot Q_{0}(a+r)+k_{2}\cdot Q_{0}(a+2r)+k_{3}\cdot Q_{0}(a+3r)\end{eqnarray}$$
$$\begin{eqnarray}(a,r)\mapsto k_{0}\cdot Q_{0}(a)+k_{1}\cdot Q_{0}(a+r)+k_{2}\cdot Q_{0}(a+2r)+k_{3}\cdot Q_{0}(a+3r)\end{eqnarray}$$
on
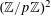 $(\mathbb{Z}/p\mathbb{Z})^{2}$
for bounded tuples
$(\mathbb{Z}/p\mathbb{Z})^{2}$
for bounded tuples
 $k_{0},k_{1},k_{2},k_{3}\in \mathbb{Z}^{d}$
vanishes if and only if
$k_{0},k_{1},k_{2},k_{3}\in \mathbb{Z}^{d}$
vanishes if and only if
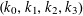 $(k_{0},k_{1},k_{2},k_{3})$
is of the form
$(k_{0},k_{1},k_{2},k_{3})$
is of the form
 $(k,-3k,3k,-k)$
for some tuple
$(k,-3k,3k,-k)$
for some tuple
![]() $k$
, where
$k$
, where
 $$\begin{eqnarray}Q_{0}(a):=\biggl(\frac{\unicode[STIX]{x1D6FC}_{1}a^{2}}{p},\ldots ,\frac{\unicode[STIX]{x1D6FC}_{d}a^{2}}{p}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}Q_{0}(a):=\biggl(\frac{\unicode[STIX]{x1D6FC}_{1}a^{2}}{p},\ldots ,\frac{\unicode[STIX]{x1D6FC}_{d}a^{2}}{p}\biggr)\end{eqnarray}$$
denotes the purely quadratic component of
![]() $Q(a)$
. Using this and a variant of the Weyl equidistribution criterion, one can eventually compute that
$Q(a)$
. Using this and a variant of the Weyl equidistribution criterion, one can eventually compute that
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f)\approx \int _{G}\int _{G}\int _{G}F(x)F(y)F(z)F(x-3y+3z)\,d\unicode[STIX]{x1D707}(x)\,d\unicode[STIX]{x1D707}(y)\,d\unicode[STIX]{x1D707}(z).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f)\approx \int _{G}\int _{G}\int _{G}F(x)F(y)F(z)F(x-3y+3z)\,d\unicode[STIX]{x1D707}(x)\,d\unicode[STIX]{x1D707}(y)\,d\unicode[STIX]{x1D707}(z).\end{eqnarray}$$
Applying Lemma 3.2, we conclude (a heuristic version of) Theorem 3.1 in this case, taking
![]() $\mathbf{a},\mathbf{r}$
to be independent uniformly distributed variables on
$\mathbf{a},\mathbf{r}$
to be independent uniformly distributed variables on
![]() $\mathbb{Z}/p\mathbb{Z}$
.
$\mathbb{Z}/p\mathbb{Z}$
.
Example 2 (A well-distributed impure quadratic factor).
Now we give a “local” version of the first example, in which the function
![]() $f$
exhibits “locally quadratic” behaviour rather than “globally quadratic” behaviour. Let
$f$
exhibits “locally quadratic” behaviour rather than “globally quadratic” behaviour. Let
![]() $\unicode[STIX]{x1D702}>0$
be a small parameter, and suppose that
$\unicode[STIX]{x1D702}>0$
be a small parameter, and suppose that
![]() $p$
is very large compared to
$p$
is very large compared to
![]() $\unicode[STIX]{x1D702}$
. We suppose that the cyclic group
$\unicode[STIX]{x1D702}$
. We suppose that the cyclic group
![]() $\mathbb{Z}/p\mathbb{Z}$
is somehow partitioned into a number
$\mathbb{Z}/p\mathbb{Z}$
is somehow partitioned into a number
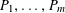 $P_{1},\ldots ,P_{m}$
of arithmetic progressions; the number
$P_{1},\ldots ,P_{m}$
of arithmetic progressions; the number
![]() $m$
of such progressions should be thought of as being moderately large (e.g.
$m$
of such progressions should be thought of as being moderately large (e.g.
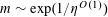 $m\sim \exp (1/\unicode[STIX]{x1D702}^{O(1)})$
for some parameter
$m\sim \exp (1/\unicode[STIX]{x1D702}^{O(1)})$
for some parameter
![]() $\unicode[STIX]{x1D702}>0$
). Consider one such progression, for example
$\unicode[STIX]{x1D702}>0$
). Consider one such progression, for example
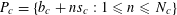 $P_{c}=\{b_{c}+ns_{c}:1\leqslant n\leqslant N_{c}\}$
for some
$P_{c}=\{b_{c}+ns_{c}:1\leqslant n\leqslant N_{c}\}$
for some
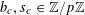 $b_{c},s_{c}\in \mathbb{Z}/p\mathbb{Z}$
and some
$b_{c},s_{c}\in \mathbb{Z}/p\mathbb{Z}$
and some
![]() $N_{c}>0$
; one should think of
$N_{c}>0$
; one should think of
![]() $N_{c}$
as being reasonably large, e.g.
$N_{c}$
as being reasonably large, e.g.
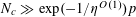 $N_{c}\gg \exp (-1/\unicode[STIX]{x1D702}^{O(1)})p$
. To each such progression
$N_{c}\gg \exp (-1/\unicode[STIX]{x1D702}^{O(1)})p$
. To each such progression
![]() $P_{c}$
, we associate a torus
$P_{c}$
, we associate a torus
 $G_{c}=(\mathbb{R}/\mathbb{Z})^{d_{c}}$
for some bounded
$G_{c}=(\mathbb{R}/\mathbb{Z})^{d_{c}}$
for some bounded
![]() $d_{c}$
with probability Haar measure
$d_{c}$
with probability Haar measure
![]() $\unicode[STIX]{x1D707}_{c}$
, a smooth function
$\unicode[STIX]{x1D707}_{c}$
, a smooth function
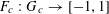 $F_{c}:G_{c}\rightarrow [-1,1]$
, and a collection
$F_{c}:G_{c}\rightarrow [-1,1]$
, and a collection
 $\unicode[STIX]{x1D709}_{c,1},\ldots ,\unicode[STIX]{x1D709}_{c,d_{c}}\in \mathbb{R}/\mathbb{Z}$
of frequencies that are generic in the sense that there does not exist any non-trivial relations of the form
$\unicode[STIX]{x1D709}_{c,1},\ldots ,\unicode[STIX]{x1D709}_{c,d_{c}}\in \mathbb{R}/\mathbb{Z}$
of frequencies that are generic in the sense that there does not exist any non-trivial relations of the form
 $$\begin{eqnarray}k_{1}\unicode[STIX]{x1D709}_{c,1}+\cdots +k_{d_{c}}\unicode[STIX]{x1D709}_{c,d_{c}}=O\biggl(\frac{1}{N_{c}}\biggr)~(\operatorname{mod}~1)\end{eqnarray}$$
$$\begin{eqnarray}k_{1}\unicode[STIX]{x1D709}_{c,1}+\cdots +k_{d_{c}}\unicode[STIX]{x1D709}_{c,d_{c}}=O\biggl(\frac{1}{N_{c}}\biggr)~(\operatorname{mod}~1)\end{eqnarray}$$
for bounded
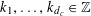 $k_{1},\ldots ,k_{d_{c}}\in \mathbb{Z}$
. We then define the function
$k_{1},\ldots ,k_{d_{c}}\in \mathbb{Z}$
. We then define the function
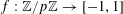 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
by setting
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
by setting
 $$\begin{eqnarray}f(b_{c}+ns_{c}):=F_{c}(\unicode[STIX]{x1D709}_{c,d_{1}}n^{2},\ldots ,\unicode[STIX]{x1D709}_{c,d_{c}}n^{2})\end{eqnarray}$$
$$\begin{eqnarray}f(b_{c}+ns_{c}):=F_{c}(\unicode[STIX]{x1D709}_{c,d_{1}}n^{2},\ldots ,\unicode[STIX]{x1D709}_{c,d_{c}}n^{2})\end{eqnarray}$$
for
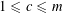 $1\leqslant c\leqslant m$
and
$1\leqslant c\leqslant m$
and
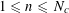 $1\leqslant n\leqslant N_{c}$
. One could also add a lower order linear term to the phases
$1\leqslant n\leqslant N_{c}$
. One could also add a lower order linear term to the phases
![]() $\unicode[STIX]{x1D709}_{c,i}n^{2}$
, as in the preceding example, if desired, but we will not do so here to simplify the exposition slightly.
$\unicode[STIX]{x1D709}_{c,i}n^{2}$
, as in the preceding example, if desired, but we will not do so here to simplify the exposition slightly.
Within each progression
![]() $P_{c}$
, a Weyl equidistribution analysis (using the genericity hypothesis) reveals that the tuple
$P_{c}$
, a Weyl equidistribution analysis (using the genericity hypothesis) reveals that the tuple
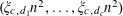 $(\unicode[STIX]{x1D709}_{c,d_{1}}n^{2},\ldots ,\unicode[STIX]{x1D709}_{c,d_{c}}n^{2})$
becomes equidistributed in
$(\unicode[STIX]{x1D709}_{c,d_{1}}n^{2},\ldots ,\unicode[STIX]{x1D709}_{c,d_{c}}n^{2})$
becomes equidistributed in
![]() $G_{c}$
as
$G_{c}$
as
![]() $p$
becomes large, so that
$p$
becomes large, so that
 $$\begin{eqnarray}\mathbb{E}_{a\in P_{c}}f(a)\approx \int _{G_{c}}F_{c}(x)\,d\unicode[STIX]{x1D707}_{c}(x).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{a\in P_{c}}f(a)\approx \int _{G_{c}}F_{c}(x)\,d\unicode[STIX]{x1D707}_{c}(x).\end{eqnarray}$$
Now we define the random variables
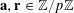 $\mathbf{a},\mathbf{r}\in \mathbb{Z}/p\mathbb{Z}$
as follows. We first select a random element
$\mathbf{a},\mathbf{r}\in \mathbb{Z}/p\mathbb{Z}$
as follows. We first select a random element
![]() $\mathbf{c}$
from
$\mathbf{c}$
from
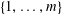 $\{1,\ldots ,m\}$
with
$\{1,\ldots ,m\}$
with
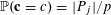 $\mathbb{P}(\mathbf{c}=c)=|P_{j}|/p$
for
$\mathbb{P}(\mathbf{c}=c)=|P_{j}|/p$
for
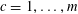 $c=1,\ldots ,m$
. Conditioning on the event that
$c=1,\ldots ,m$
. Conditioning on the event that
![]() $\mathbf{c}$
is equal to
$\mathbf{c}$
is equal to
![]() $c$
, we then select
$c$
, we then select
![]() $\mathbf{a}$
uniformly at random from
$\mathbf{a}$
uniformly at random from
![]() $P_{c}$
, and also select
$P_{c}$
, and also select
![]() $\mathbf{r}$
uniformly at random from an arithmetic progression of the form
$\mathbf{r}$
uniformly at random from an arithmetic progression of the form
 $$\begin{eqnarray}\{ns_{c}:|n|\leqslant \exp (-1/\unicode[STIX]{x1D702}^{-C})N_{c}\},\end{eqnarray}$$
$$\begin{eqnarray}\{ns_{c}:|n|\leqslant \exp (-1/\unicode[STIX]{x1D702}^{-C})N_{c}\},\end{eqnarray}$$
with
![]() $\mathbf{a}$
and
$\mathbf{a}$
and
![]() $\mathbf{r}$
independent after conditioning on
$\mathbf{r}$
independent after conditioning on
![]() $\mathbf{c}=c$
. Note that
$\mathbf{c}=c$
. Note that
![]() $\mathbf{a}$
and
$\mathbf{a}$
and
![]() $\mathbf{r}$
are only conditionally independent, relative to the auxiliary variable
$\mathbf{r}$
are only conditionally independent, relative to the auxiliary variable
![]() $\mathbf{c}$
; if one does not perform this conditioning, then
$\mathbf{c}$
; if one does not perform this conditioning, then
![]() $\mathbf{a}$
and
$\mathbf{a}$
and
![]() $\mathbf{r}$
become coupled to each other through their mutual dependence on
$\mathbf{r}$
become coupled to each other through their mutual dependence on
![]() $\mathbf{c}$
.
$\mathbf{c}$
.
Without conditioning on
![]() $\mathbf{c}$
, the random variable
$\mathbf{c}$
, the random variable
![]() $\mathbf{a}$
becomes uniformly distributed on
$\mathbf{a}$
becomes uniformly distributed on
![]() $\mathbb{Z}/p\mathbb{Z}$
, thus
$\mathbb{Z}/p\mathbb{Z}$
, thus
 $$\begin{eqnarray}\mathbb{E}f(\mathbf{a})=\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}f(a).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f(\mathbf{a})=\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}f(a).\end{eqnarray}$$
Also, from (3.11) we have the conditional expectation
 $$\begin{eqnarray}\mathbb{E}(f(\mathbf{a})|\mathbf{c}=c)\approx \int _{G_{c}}F_{c}(x)\,d\unicode[STIX]{x1D707}_{c}(x).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}(f(\mathbf{a})|\mathbf{c}=c)\approx \int _{G_{c}}F_{c}(x)\,d\unicode[STIX]{x1D707}_{c}(x).\end{eqnarray}$$
A modification of the equidistribution analysis from the first example also gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f|\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad \gtrapprox \int _{G_{c}}\int _{G_{c}}\int _{G_{c}}F_{c}(x)F_{c}(y)F_{c}(z)F(x-3y+3z)\,d\unicode[STIX]{x1D707}_{c}(x)\,d\unicode[STIX]{x1D707}_{c}(y)\,d\unicode[STIX]{x1D707}_{c}(z),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f|\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad \gtrapprox \int _{G_{c}}\int _{G_{c}}\int _{G_{c}}F_{c}(x)F_{c}(y)F_{c}(z)F(x-3y+3z)\,d\unicode[STIX]{x1D707}_{c}(x)\,d\unicode[STIX]{x1D707}_{c}(y)\,d\unicode[STIX]{x1D707}_{c}(z),\nonumber\end{eqnarray}$$
where the conditional quartic form
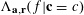 $\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f|\mathbf{c}=c)$
was defined in (3.1), and hence by Lemma 3.2 we have
$\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f|\mathbf{c}=c)$
was defined in (3.1), and hence by Lemma 3.2 we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f|\mathbf{c}=c)\gtrapprox (\mathbb{E}(f(\mathbf{a})|\mathbf{c}=c))^{4}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f|\mathbf{c}=c)\gtrapprox (\mathbb{E}(f(\mathbf{a})|\mathbf{c}=c))^{4}.\end{eqnarray}$$
Averaging in
![]() $c$
(weighted by
$c$
(weighted by
 $\mathbb{P}(\mathbf{c}=c)$
) to remove the conditional expectation on the left-hand side, and then applying Hölder’s inequality, we obtain a heuristic version of Theorem 3.1 in this case.
$\mathbb{P}(\mathbf{c}=c)$
) to remove the conditional expectation on the left-hand side, and then applying Hölder’s inequality, we obtain a heuristic version of Theorem 3.1 in this case.
Example 3 (A poorly distributed pure quadratic factor).
We now return to the situation of the first example, except that we no longer impose the genericity hypothesis, that is to say we allow for a non-trivial relation of the form (3.7). Without loss of generality we can take the coefficient
![]() $k_{d}$
of this relation to be non-zero. Because of this relation, the quantity
$k_{d}$
of this relation to be non-zero. Because of this relation, the quantity
![]() $Q(\mathbf{a})$
studied in the first example and the tuple (3.8) may not necessarily be as equidistributed as before. However, we can use this irregularity of distribution to modify the representation of
$Q(\mathbf{a})$
studied in the first example and the tuple (3.8) may not necessarily be as equidistributed as before. However, we can use this irregularity of distribution to modify the representation of
![]() $f$
(up to a small error) in such a manner as to reduce the number
$f$
(up to a small error) in such a manner as to reduce the number
![]() $d$
of quadratic phases involved. Namely, we can write
$d$
of quadratic phases involved. Namely, we can write
 $$\begin{eqnarray}f(a):=\tilde{F}\biggl(\tilde{Q}(a),\frac{\unicode[STIX]{x1D6FE}a}{p}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}f(a):=\tilde{F}\biggl(\tilde{Q}(a),\frac{\unicode[STIX]{x1D6FE}a}{p}\biggr)\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle \tilde{Q}(a) & := & \displaystyle \biggl(\frac{k_{d}^{-1}\unicode[STIX]{x1D6FC}_{1}a^{2}+k_{d}^{-1}\unicode[STIX]{x1D6FD}_{1}a}{p},\ldots ,\frac{k_{d}^{-1}\unicode[STIX]{x1D6FC}_{d-1}a^{2}+k_{d}^{-1}\unicode[STIX]{x1D6FD}_{d-1}a}{p}\biggr),\nonumber\\ \displaystyle \unicode[STIX]{x1D6FE} & := & \displaystyle \unicode[STIX]{x1D6FD}_{d}+k_{1}k_{d}^{-1}\unicode[STIX]{x1D6FD}_{1}+\cdots +k_{d-1}k_{d}^{-1}\unicode[STIX]{x1D6FD}_{d-1},\nonumber\\ \displaystyle \tilde{F}(x_{1},\ldots ,x_{d-1},y) & := & \displaystyle F(k_{d}x_{1},\ldots ,k_{d}x_{d-1},-k_{1}x_{1}-\cdots -k_{d-1}x_{d-1}+y)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{Q}(a) & := & \displaystyle \biggl(\frac{k_{d}^{-1}\unicode[STIX]{x1D6FC}_{1}a^{2}+k_{d}^{-1}\unicode[STIX]{x1D6FD}_{1}a}{p},\ldots ,\frac{k_{d}^{-1}\unicode[STIX]{x1D6FC}_{d-1}a^{2}+k_{d}^{-1}\unicode[STIX]{x1D6FD}_{d-1}a}{p}\biggr),\nonumber\\ \displaystyle \unicode[STIX]{x1D6FE} & := & \displaystyle \unicode[STIX]{x1D6FD}_{d}+k_{1}k_{d}^{-1}\unicode[STIX]{x1D6FD}_{1}+\cdots +k_{d-1}k_{d}^{-1}\unicode[STIX]{x1D6FD}_{d-1},\nonumber\\ \displaystyle \tilde{F}(x_{1},\ldots ,x_{d-1},y) & := & \displaystyle F(k_{d}x_{1},\ldots ,k_{d}x_{d-1},-k_{1}x_{1}-\cdots -k_{d-1}x_{d-1}+y)\nonumber\end{eqnarray}$$
and where we take advantage of the field structure of
![]() $\mathbb{Z}/p\mathbb{Z}$
to locate an inverse
$\mathbb{Z}/p\mathbb{Z}$
to locate an inverse
![]() $k_{d}^{-1}$
of
$k_{d}^{-1}$
of
![]() $k_{d}$
in this field. For our quantitative analysis we will run into a technical difficulty with this representation, in that the Lipschitz constant of
$k_{d}$
in this field. For our quantitative analysis we will run into a technical difficulty with this representation, in that the Lipschitz constant of
![]() $\tilde{F}$
will increase by an undesirable amount compared to that of
$\tilde{F}$
will increase by an undesirable amount compared to that of
![]() $F$
when one performs this change of variable, at least if one uses the standard metric on the torus. To fix this, we will eventually have to work with more general tori
$F$
when one performs this change of variable, at least if one uses the standard metric on the torus. To fix this, we will eventually have to work with more general tori
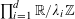 $\prod _{i=1}^{d}\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}$
than the standard torus
$\prod _{i=1}^{d}\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}$
than the standard torus
![]() $(\mathbb{R}/\mathbb{Z})^{d}$
, but we ignore this issue for now to continue with the heuristic discussion.
$(\mathbb{R}/\mathbb{Z})^{d}$
, but we ignore this issue for now to continue with the heuristic discussion.
To remove the dependence on the linear phase
![]() $\unicode[STIX]{x1D6FE}a/p$
, we partition
$\unicode[STIX]{x1D6FE}a/p$
, we partition
![]() $\mathbb{Z}/p\mathbb{Z}$
into “(shifted) Bohr sets”
$\mathbb{Z}/p\mathbb{Z}$
into “(shifted) Bohr sets”
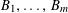 $B_{1},\ldots ,B_{m}$
for some moderately large
$B_{1},\ldots ,B_{m}$
for some moderately large
![]() $m$
(e.g.
$m$
(e.g.
 $m\sim \exp (1/\unicode[STIX]{x1D702}^{-C})$
for some constant
$m\sim \exp (1/\unicode[STIX]{x1D702}^{-C})$
for some constant
![]() $C>0$
), defined by
$C>0$
), defined by
 $$\begin{eqnarray}B_{c}:=\biggl\{a\in \mathbb{Z}/p\mathbb{Z}:\frac{\unicode[STIX]{x1D6FE}a}{p}\in \biggl[\frac{c-1}{m},\frac{c}{m}\biggr)~(\operatorname{mod}~1)\biggr\}\end{eqnarray}$$
$$\begin{eqnarray}B_{c}:=\biggl\{a\in \mathbb{Z}/p\mathbb{Z}:\frac{\unicode[STIX]{x1D6FE}a}{p}\in \biggl[\frac{c-1}{m},\frac{c}{m}\biggr)~(\operatorname{mod}~1)\biggr\}\end{eqnarray}$$
for
 $c=1,\ldots ,m$
. On each Bohr set
$c=1,\ldots ,m$
. On each Bohr set
![]() $B_{c}$
, we have the approximation
$B_{c}$
, we have the approximation
 $$\begin{eqnarray}f(a):=\tilde{F}_{c}(\tilde{Q}(a))\end{eqnarray}$$
$$\begin{eqnarray}f(a):=\tilde{F}_{c}(\tilde{Q}(a))\end{eqnarray}$$
where
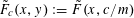 $\tilde{F}_{c}(x,y):=\tilde{F}(x,c/m)$
. Using the heuristic that Bohr sets behave like arithmetic progressions, the situation is now similar to that in the second example, with the number of quadratic phases involved reduced from
$\tilde{F}_{c}(x,y):=\tilde{F}(x,c/m)$
. Using the heuristic that Bohr sets behave like arithmetic progressions, the situation is now similar to that in the second example, with the number of quadratic phases involved reduced from
![]() $d$
to
$d$
to
![]() $d-1$
, except that there may still be some non-trivial relations among the surviving quadratic phases (and one also now has some lower order linear terms in the quadratic phases). To deal with this difficulty, we turn now to the consideration of yet another example.
$d-1$
, except that there may still be some non-trivial relations among the surviving quadratic phases (and one also now has some lower order linear terms in the quadratic phases). To deal with this difficulty, we turn now to the consideration of yet another example.
Example 4 (A poorly distributed impure quadratic factor).
We now consider an example that is in some sense a combination of the second and third examples. Namely, we suppose we are in the same situation as in the second example, except that we allow some of the indices
![]() $c$
to have “poor quadratic distribution” in the sense that they admit non-trivial relations of the form (3.10). Again we may assume without loss of generality that
$c$
to have “poor quadratic distribution” in the sense that they admit non-trivial relations of the form (3.10). Again we may assume without loss of generality that
![]() $k_{d_{c}}$
is non-zero in such relations. Because of such relations, we no longer expect to have the equidistribution properties that were used in the second example. However, by modifying the calculations in the third example, we can obtain a new representation of
$k_{d_{c}}$
is non-zero in such relations. Because of such relations, we no longer expect to have the equidistribution properties that were used in the second example. However, by modifying the calculations in the third example, we can obtain a new representation of
![]() $f$
(again allowing for a small error) on each of the progressions
$f$
(again allowing for a small error) on each of the progressions
![]() $P_{c}$
with poor quadratic distribution to reduce the number
$P_{c}$
with poor quadratic distribution to reduce the number
![]() $d_{c}$
of quadratic polynomials used in that progression by one. Iterating this process a finite number of times, one eventually returns to the situation in the second example in which no non-trivial relations occur, at which point one can (heuristically, at least) verify Theorem 3.1 in this case.
$d_{c}$
of quadratic polynomials used in that progression by one. Iterating this process a finite number of times, one eventually returns to the situation in the second example in which no non-trivial relations occur, at which point one can (heuristically, at least) verify Theorem 3.1 in this case.
The situation becomes slightly more complicated if one adds a lower order linear term
![]() $\unicode[STIX]{x1D701}_{c,i}n$
to the purely quadratic phases
$\unicode[STIX]{x1D701}_{c,i}n$
to the purely quadratic phases
![]() $\unicode[STIX]{x1D709}_{c,i}n^{2}$
appearing in the second example; this basically is the type of situation one encounters for instance at the conclusion of the third example. In this case, every time one converts a non-trivial relation of the form (3.10) on one of the cells
$\unicode[STIX]{x1D709}_{c,i}n^{2}$
appearing in the second example; this basically is the type of situation one encounters for instance at the conclusion of the third example. In this case, every time one converts a non-trivial relation of the form (3.10) on one of the cells
![]() $P_{c}$
of the partition into a new representation of
$P_{c}$
of the partition into a new representation of
![]() $f$
on that cell, one must subdivide that cell
$f$
on that cell, one must subdivide that cell
![]() $P_{j}$
into smaller pieces, by intersecting
$P_{j}$
into smaller pieces, by intersecting
![]() $P_{j}$
with various Bohr sets. However, the resulting sets still behave somewhat like arithmetic progressions, and it turns out that we can still iterate the construction a bounded number of times until no further non-trivial relations between surviving quadratic phases remain on any of the cells of the partition, at which point one can (heuristically, at least) verify Theorem 3.1 in this case (as well as in the case considered in the third example).
$P_{j}$
with various Bohr sets. However, the resulting sets still behave somewhat like arithmetic progressions, and it turns out that we can still iterate the construction a bounded number of times until no further non-trivial relations between surviving quadratic phases remain on any of the cells of the partition, at which point one can (heuristically, at least) verify Theorem 3.1 in this case (as well as in the case considered in the third example).
Example 5 (A pseudorandom perturbation of a pure quadratic factor).
In all the preceding examples, the function
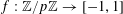 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
under consideration was “locally quadratically structured”, in the sense that on local regions such as
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
under consideration was “locally quadratically structured”, in the sense that on local regions such as
![]() $P_{c}$
, the function
$P_{c}$
, the function
![]() $f$
could be accurately represented in terms of quadratic phase functions
$f$
could be accurately represented in terms of quadratic phase functions
 $a\mapsto Q(a)$
. This is however not the typical behaviour expected for a general function
$a\mapsto Q(a)$
. This is however not the typical behaviour expected for a general function
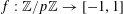 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
. A more representative example would be a function of the form
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
. A more representative example would be a function of the form
 $$\begin{eqnarray}f(a):=f_{1}(a)+f_{2}(a),\end{eqnarray}$$
$$\begin{eqnarray}f(a):=f_{1}(a)+f_{2}(a),\end{eqnarray}$$
where
 $f_{1}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{R}$
is a function of the type considered in the first example, thus
$f_{1}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{R}$
is a function of the type considered in the first example, thus
 $$\begin{eqnarray}f_{1}(a)=F(Q(a))\end{eqnarray}$$
$$\begin{eqnarray}f_{1}(a)=F(Q(a))\end{eqnarray}$$
for some quadratic function
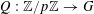 $Q:\mathbb{Z}/p\mathbb{Z}\rightarrow G$
into a torus
$Q:\mathbb{Z}/p\mathbb{Z}\rightarrow G$
into a torus
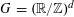 $G=(\mathbb{R}/\mathbb{Z})^{d}$
and some smooth
$G=(\mathbb{R}/\mathbb{Z})^{d}$
and some smooth
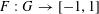 $F:G\rightarrow [-1,1]$
, and
$F:G\rightarrow [-1,1]$
, and
 $f_{2}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
is a function that is globally Gowers uniform in the sense that
$f_{2}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
is a function that is globally Gowers uniform in the sense that
 $$\begin{eqnarray}\mathbb{E}\mathop{\prod }_{(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}}f_{2}(\mathbf{a}+\unicode[STIX]{x1D714}_{1}\mathbf{h}_{1}+\unicode[STIX]{x1D714}_{2}\mathbf{h}_{2}+\unicode[STIX]{x1D714}_{3}\mathbf{h}_{3})\approx 0,\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}\mathop{\prod }_{(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}}f_{2}(\mathbf{a}+\unicode[STIX]{x1D714}_{1}\mathbf{h}_{1}+\unicode[STIX]{x1D714}_{2}\mathbf{h}_{2}+\unicode[STIX]{x1D714}_{3}\mathbf{h}_{3})\approx 0,\end{eqnarray}$$
where
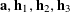 $\mathbf{a},\mathbf{h}_{1},\mathbf{h}_{2},\mathbf{h}_{3}$
are drawn independently and uniformly at random from
$\mathbf{a},\mathbf{h}_{1},\mathbf{h}_{2},\mathbf{h}_{3}$
are drawn independently and uniformly at random from
![]() $\mathbb{Z}/p\mathbb{Z}$
. A typical example to keep in mind is when
$\mathbb{Z}/p\mathbb{Z}$
. A typical example to keep in mind is when
![]() $F$
(and hence
$F$
(and hence
![]() $f_{1}$
) takes values in
$f_{1}$
) takes values in
![]() $[0,1]$
, and
$[0,1]$
, and
![]() $f=\mathbf{f}$
is a random function with
$f=\mathbf{f}$
is a random function with
![]() $f(a)$
equal to
$f(a)$
equal to
![]() $1$
with probability
$1$
with probability
![]() $f_{1}(a)$
and
$f_{1}(a)$
and
![]() $0$
with probability
$0$
with probability
 $1-f_{1}(a)$
, independently as
$1-f_{1}(a)$
, independently as
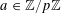 $a\in \mathbb{Z}/p\mathbb{Z}$
varies; then the
$a\in \mathbb{Z}/p\mathbb{Z}$
varies; then the
![]() $f_{2}(a)$
for
$f_{2}(a)$
for
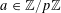 $a\in \mathbb{Z}/p\mathbb{Z}$
become independent random variables of mean zero, and the global Gowers uniformity can be established with high probability using tools such as the Chernoff inequality.
$a\in \mathbb{Z}/p\mathbb{Z}$
become independent random variables of mean zero, and the global Gowers uniformity can be established with high probability using tools such as the Chernoff inequality.
From the standard theory of the Gowers norms (see e.g. [Reference Tao and Vu33, Ch. 11]), one can use the global Gowers uniformity of
![]() $f_{2}$
, combined with a number of applications of the Cauchy–Schwarz inequality, to establish a “generalized von Neumann theorem” that, in our current context, implies that
$f_{2}$
, combined with a number of applications of the Cauchy–Schwarz inequality, to establish a “generalized von Neumann theorem” that, in our current context, implies that
![]() $f$
and
$f$
and
![]() $f_{1}$
globally count approximately the same number of length-four progressions in the sense that
$f_{1}$
globally count approximately the same number of length-four progressions in the sense that
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f)\approx \unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f_{1});\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f)\approx \unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f_{1});\end{eqnarray}$$
similarly one also has
 $$\begin{eqnarray}\mathbb{E}f(\mathbf{a})\approx \mathbb{E}f_{1}(\mathbf{a}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f(\mathbf{a})\approx \mathbb{E}f_{1}(\mathbf{a}).\end{eqnarray}$$
As a consequence, Theorem 3.1 for such functions follows (heuristically, at least) from the analysis of the first example, at least if one assumes the genericity of the frequencies
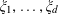 $\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{d}$
.
$\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{d}$
.
Example 6 (A pseudorandom perturbation of an impure quadratic factor).
We now consider a situation that is to the second example as the fifth example was to the first. Namely, we consider a function of the form
 $$\begin{eqnarray}f(a):=f_{1}(a)+f_{2}(a),\end{eqnarray}$$
$$\begin{eqnarray}f(a):=f_{1}(a)+f_{2}(a),\end{eqnarray}$$
where
 $f_{1}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
is a function of the type considered in the second example, thus
$f_{1}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
is a function of the type considered in the second example, thus
 $$\begin{eqnarray}f_{1}(b_{c}+ns_{c}):=F_{c}(\unicode[STIX]{x1D709}_{c,d_{1}}n^{2},\ldots ,\unicode[STIX]{x1D709}_{c,d_{c}}n^{2})\end{eqnarray}$$
$$\begin{eqnarray}f_{1}(b_{c}+ns_{c}):=F_{c}(\unicode[STIX]{x1D709}_{c,d_{1}}n^{2},\ldots ,\unicode[STIX]{x1D709}_{c,d_{c}}n^{2})\end{eqnarray}$$
for
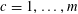 $c=1,\ldots ,m$
and
$c=1,\ldots ,m$
and
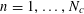 $n=1,\ldots ,N_{c}$
. As for the function
$n=1,\ldots ,N_{c}$
. As for the function
 $f_{2}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
, global Gowers uniformity of
$f_{2}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
, global Gowers uniformity of
![]() $f_{2}$
will be too weak of a hypothesis for our purposes, because the random variable
$f_{2}$
will be too weak of a hypothesis for our purposes, because the random variable
![]() $\mathbf{r}$
appearing in the second example is now localized to a significantly smaller region than
$\mathbf{r}$
appearing in the second example is now localized to a significantly smaller region than
![]() $\mathbb{Z}/p\mathbb{Z}$
. Instead, we will require the local Gowers uniformity hypothesis
$\mathbb{Z}/p\mathbb{Z}$
. Instead, we will require the local Gowers uniformity hypothesis
 $$\begin{eqnarray}\mathbb{E}\mathop{\prod }_{(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}}f_{2}(\mathbf{a}+\unicode[STIX]{x1D714}_{1}\mathbf{h}_{1}+\unicode[STIX]{x1D714}_{2}\mathbf{h}_{2}+\unicode[STIX]{x1D714}_{3}\mathbf{h}_{3})\approx 0,\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}\mathop{\prod }_{(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}}f_{2}(\mathbf{a}+\unicode[STIX]{x1D714}_{1}\mathbf{h}_{1}+\unicode[STIX]{x1D714}_{2}\mathbf{h}_{2}+\unicode[STIX]{x1D714}_{3}\mathbf{h}_{3})\approx 0,\end{eqnarray}$$
where
![]() $\mathbf{a}$
is now the random variable from the second example (in particular,
$\mathbf{a}$
is now the random variable from the second example (in particular,
![]() $\mathbf{a}$
depends on the auxiliary random variable
$\mathbf{a}$
depends on the auxiliary random variable
![]() $\mathbf{c}$
), and once one conditions on an event
$\mathbf{c}$
), and once one conditions on an event
![]() $\mathbf{c}=c$
for
$\mathbf{c}=c$
for
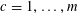 $c=1,\ldots ,m$
, one draws
$c=1,\ldots ,m$
, one draws
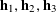 $\mathbf{h}_{1},\mathbf{h}_{2},\mathbf{h}_{3}$
independently of each other and from
$\mathbf{h}_{1},\mathbf{h}_{2},\mathbf{h}_{3}$
independently of each other and from
![]() $\mathbf{a}$
, and each
$\mathbf{a}$
, and each
![]() $\mathbf{h}_{i}$
drawn uniformly from an arithmetic progression of the form
$\mathbf{h}_{i}$
drawn uniformly from an arithmetic progression of the form
 $$\begin{eqnarray}\{ns_{c}:|n|\leqslant \exp (-1/\unicode[STIX]{x1D702}^{-C_{i}})N_{c}\},\end{eqnarray}$$
$$\begin{eqnarray}\{ns_{c}:|n|\leqslant \exp (-1/\unicode[STIX]{x1D702}^{-C_{i}})N_{c}\},\end{eqnarray}$$
for some constant
![]() $C_{i}>0$
(for technical reasons, it is convenient to allow these constants
$C_{i}>0$
(for technical reasons, it is convenient to allow these constants
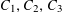 $C_{1},C_{2},C_{3}$
to be different from each other, and also to be larger than the constant
$C_{1},C_{2},C_{3}$
to be different from each other, and also to be larger than the constant
![]() $C$
appearing in (3.12), so that
$C$
appearing in (3.12), so that
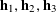 $\mathbf{h}_{1},\mathbf{h}_{2},\mathbf{h}_{3}$
range over a narrower scale than
$\mathbf{h}_{1},\mathbf{h}_{2},\mathbf{h}_{3}$
range over a narrower scale than
![]() $\mathbf{r}$
). As with
$\mathbf{r}$
). As with
![]() $\mathbf{a}$
and
$\mathbf{a}$
and
![]() $\mathbf{r}$
, the random variables
$\mathbf{r}$
, the random variables
 $\mathbf{a},\mathbf{h}_{1},\mathbf{h}_{2},\mathbf{h}_{3}$
are now only conditionally independent relative to the auxiliary variable
$\mathbf{a},\mathbf{h}_{1},\mathbf{h}_{2},\mathbf{h}_{3}$
are now only conditionally independent relative to the auxiliary variable
![]() $\mathbf{c}$
, but are not independent of each other without this conditioning, as they are coupled to each other through
$\mathbf{c}$
, but are not independent of each other without this conditioning, as they are coupled to each other through
![]() $\mathbf{c}$
.
$\mathbf{c}$
.
As it turns out, once one assumes this local Gowers uniformity of
![]() $f_{2}$
, one can modify the Cauchy–Schwarz arguments used to establish the global generalized von Neumann theorem to obtain the approximations (3.14), (3.15) for the random variables
$f_{2}$
, one can modify the Cauchy–Schwarz arguments used to establish the global generalized von Neumann theorem to obtain the approximations (3.14), (3.15) for the random variables
![]() $\mathbf{a},\mathbf{r}$
considered in the second example, at which point Theorem 3.1 for this choice of
$\mathbf{a},\mathbf{r}$
considered in the second example, at which point Theorem 3.1 for this choice of
![]() $f$
follows (heuristically, at least) from the analysis of that example, at least if one assumes that there are no non-trivial relations of the form (3.10).
$f$
follows (heuristically, at least) from the analysis of that example, at least if one assumes that there are no non-trivial relations of the form (3.10).
Example 7 (Non-pseudorandom perturbation of a pure quadratic factor).
We now modify the fifth example by replacing the hypothesis (3.13) by its negation
 $$\begin{eqnarray}\mathbb{E}\mathop{\prod }_{(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}}f_{2}(\mathbf{a}+\unicode[STIX]{x1D714}_{1}\mathbf{h}_{1}+\unicode[STIX]{x1D714}_{2}\mathbf{h}_{2}+\unicode[STIX]{x1D714}_{3}\mathbf{h}_{3})\gg 1\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}\mathop{\prod }_{(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}}f_{2}(\mathbf{a}+\unicode[STIX]{x1D714}_{1}\mathbf{h}_{1}+\unicode[STIX]{x1D714}_{2}\mathbf{h}_{2}+\unicode[STIX]{x1D714}_{3}\mathbf{h}_{3})\gg 1\end{eqnarray}$$
(it is not difficult to show that the left-hand side is non-negative). In this case, the generalized von Neumann theorem used in that example does not give a good estimate. However, in this situation one can apply the inverse theorem for the Gowers norm established by us in [Reference Green and Tao14]. To obtain good quantitative bounds, we will use the version of that theorem that involves local correlation with quadratic objects (as opposed to a somewhat weak global correlation with a single “locally quadratic” object). Namely, if (3.18) holds, then one can partition
![]() $\mathbb{Z}/p\mathbb{Z}$
into a moderately large (e.g.
$\mathbb{Z}/p\mathbb{Z}$
into a moderately large (e.g.
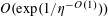 $O(\exp (1/\unicode[STIX]{x1D702}^{-O(1)}))$
) number of pieces
$O(\exp (1/\unicode[STIX]{x1D702}^{-O(1)}))$
) number of pieces
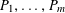 $P_{1},\ldots ,P_{m}$
, such that on each piece
$P_{1},\ldots ,P_{m}$
, such that on each piece
![]() $P_{c}$
, the function
$P_{c}$
, the function
![]() $f_{2}$
correlates with a “quadratically structured” object. The precise statement is somewhat technical to state, but one simple special case of this conclusion is that the pieces
$f_{2}$
correlates with a “quadratically structured” object. The precise statement is somewhat technical to state, but one simple special case of this conclusion is that the pieces
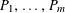 $P_{1},\ldots ,P_{m}$
are arithmetic progressions as in the second example, and for a “significant number” of the progressions
$P_{1},\ldots ,P_{m}$
are arithmetic progressions as in the second example, and for a “significant number” of the progressions
 $$\begin{eqnarray}P_{c}=\{b_{c}+ns_{c}:1\leqslant n\leqslant N_{c}\}\end{eqnarray}$$
$$\begin{eqnarray}P_{c}=\{b_{c}+ns_{c}:1\leqslant n\leqslant N_{c}\}\end{eqnarray}$$
there exists a frequency
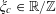 $\unicode[STIX]{x1D709}_{c}\in \mathbb{R}/\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}_{c}\in \mathbb{R}/\mathbb{Z}$
such that
 $$\begin{eqnarray}|\mathbb{E}_{1\leqslant n\leqslant N_{c}}f_{2}(b_{c}+ns_{c})e(-\unicode[STIX]{x1D709}_{c}n^{2})|\gg 1.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}_{1\leqslant n\leqslant N_{c}}f_{2}(b_{c}+ns_{c})e(-\unicode[STIX]{x1D709}_{c}n^{2})|\gg 1.\end{eqnarray}$$
(In general, one would take
![]() $P_{c}$
to be Bohr sets of moderately high rank, rather than arithmetic progressions, and the phase
$P_{c}$
to be Bohr sets of moderately high rank, rather than arithmetic progressions, and the phase
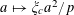 $a\mapsto \unicode[STIX]{x1D709}_{c}a^{2}/p$
would have to be replaced by a more general locally quadratic phase function on such a Bohr set, but we ignore these technicalities for the current informal discussion.) From this and the cosine rule, it is possible to find a function
$a\mapsto \unicode[STIX]{x1D709}_{c}a^{2}/p$
would have to be replaced by a more general locally quadratic phase function on such a Bohr set, but we ignore these technicalities for the current informal discussion.) From this and the cosine rule, it is possible to find a function
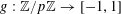 $g:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
that is equal to (the real part of) a scalar multiple of the quadratic phases
$g:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
that is equal to (the real part of) a scalar multiple of the quadratic phases
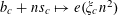 $b_{c}+ns_{c}\mapsto e(\unicode[STIX]{x1D709}_{c}n^{2})$
on each progression
$b_{c}+ns_{c}\mapsto e(\unicode[STIX]{x1D709}_{c}n^{2})$
on each progression
![]() $P_{c}$
, such that
$P_{c}$
, such that
![]() $f_{2}+g$
has an energy decrement compared to
$f_{2}+g$
has an energy decrement compared to
![]() $f_{2}$
in the sense that
$f_{2}$
in the sense that
 $$\begin{eqnarray}\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}(f_{2}(a)+g(a))^{2}\leqslant \mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}f_{2}(a)^{2}-\unicode[STIX]{x1D702}^{C}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}(f_{2}(a)+g(a))^{2}\leqslant \mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}f_{2}(a)^{2}-\unicode[STIX]{x1D702}^{C}\end{eqnarray}$$
for some constant
![]() $C>0$
. In this situation, we can modify the decomposition
$C>0$
. In this situation, we can modify the decomposition
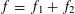 $f=f_{1}+f_{2}$
by adding
$f=f_{1}+f_{2}$
by adding
![]() $g$
to
$g$
to
![]() $f_{2}$
and subtracting it from
$f_{2}$
and subtracting it from
![]() $f_{1}$
. (Strictly speaking, this may make
$f_{1}$
. (Strictly speaking, this may make
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
range slightly outside of
$f_{2}$
range slightly outside of
![]() $[-1,1]$
, but because
$[-1,1]$
, but because
![]() $f$
itself ranges in
$f$
itself ranges in
![]() $[-1,1]$
, it turns out to be relatively easy to modify
$[-1,1]$
, it turns out to be relatively easy to modify
![]() $f_{1},f_{2}$
further to rectify this problem.) The new function
$f_{1},f_{2}$
further to rectify this problem.) The new function
![]() $f_{1}$
has a similar “quadratic structure” to the previous function
$f_{1}$
has a similar “quadratic structure” to the previous function
![]() $f_{1}$
, except that the quadratic structure is now localized to the cells
$f_{1}$
, except that the quadratic structure is now localized to the cells
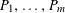 $P_{1},\ldots ,P_{m}$
of the partition of
$P_{1},\ldots ,P_{m}$
of the partition of
![]() $\mathbb{Z}/p\mathbb{Z}$
, and the number of quadratic functions has been increased by one. If the new function
$\mathbb{Z}/p\mathbb{Z}$
, and the number of quadratic functions has been increased by one. If the new function
![]() $f_{2}$
is now locally Gowers uniform in the sense of (3.16), then we are now essentially in the situation of the sixth example (at least if there are no non-trivial relations of the form (3.10)), and we can (heuristically at least) conclude Theorem 3.1 in this case by the previous analysis. If
$f_{2}$
is now locally Gowers uniform in the sense of (3.16), then we are now essentially in the situation of the sixth example (at least if there are no non-trivial relations of the form (3.10)), and we can (heuristically at least) conclude Theorem 3.1 in this case by the previous analysis. If
![]() $f_{2}$
is locally Gowers uniform but there are additionally some relations of the form (3.10), then one can hope to adapt the analysis of the fourth example to reduce the quadratic complexity of
$f_{2}$
is locally Gowers uniform but there are additionally some relations of the form (3.10), then one can hope to adapt the analysis of the fourth example to reduce the quadratic complexity of
![]() $f_{1}$
on all the poorly distributed cells, at which point one restarts the analysis. If however
$f_{1}$
on all the poorly distributed cells, at which point one restarts the analysis. If however
![]() $f_{2}$
remains non-uniform, then we need to argue using the analysis of the next and final example.
$f_{2}$
remains non-uniform, then we need to argue using the analysis of the next and final example.
Example 8 (Non-pseudorandom perturbation of an impure quadratic factor).
Our final and most difficult example will be as to the sixth example as the seventh example was to the fifth. Namely, we modify the sixth example by assuming that the negation of (3.16) holds. Equivalently, one has the lower bound
 $$\begin{eqnarray}\mathbb{E}\biggl(\mathop{\prod }_{(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}}f_{2}(\mathbf{a}+\unicode[STIX]{x1D714}_{1}\mathbf{h}_{1}+\unicode[STIX]{x1D714}_{2}\mathbf{h}_{2}+\unicode[STIX]{x1D714}_{3}\mathbf{h}_{3})|\mathbf{c}=c\biggr)\gg 1\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}\biggl(\mathop{\prod }_{(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}}f_{2}(\mathbf{a}+\unicode[STIX]{x1D714}_{1}\mathbf{h}_{1}+\unicode[STIX]{x1D714}_{2}\mathbf{h}_{2}+\unicode[STIX]{x1D714}_{3}\mathbf{h}_{3})|\mathbf{c}=c\biggr)\gg 1\end{eqnarray}$$
on the local Gowers norm for a “significant fraction” of the
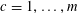 $c=1,\ldots ,m$
.
$c=1,\ldots ,m$
.
At the qualitative level, the inverse theorem in [Reference Green and Tao14] for the global Gowers norm allows one to also deduce a similar conclusion starting from the hypothesis (3.20). However, the quantitative bounds obtained by this approach turn out to be too poor for the purposes of establishing Theorems 3.1 or 1.1. Instead, one must obtain a quantitative local inverse theorem for the Gowers norm that has reasonably good bounds (of polynomial type) on the amount of correlation that is (locally) attained. Establishing such a theorem is by far the most complicated and lengthy component of this paper, although broadly speaking it follows the same strategy as previous theorems of this type in [Reference Gowers11, Reference Green and Tao14]. If one takes this local inverse theorem for granted, then roughly speaking what we can then conclude from the hypothesis (3.20) is that for a significant number of
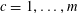 $c=1,\ldots ,m$
, one can partition the cell
$c=1,\ldots ,m$
, one can partition the cell
![]() $P_{c}$
into subcells
$P_{c}$
into subcells
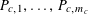 $P_{c,1},\ldots ,P_{c,m_{c}}$
, and locate a “locally quadratic phase function”
$P_{c,1},\ldots ,P_{c,m_{c}}$
, and locate a “locally quadratic phase function”
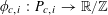 $\unicode[STIX]{x1D719}_{c,i}:P_{c,i}\rightarrow \mathbb{R}/\mathbb{Z}$
on each such subcell (generalizing the functions
$\unicode[STIX]{x1D719}_{c,i}:P_{c,i}\rightarrow \mathbb{R}/\mathbb{Z}$
on each such subcell (generalizing the functions
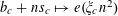 $b_{c}+ns_{c}\mapsto e(\unicode[STIX]{x1D709}_{c}n^{2})$
from the previous example), such that
$b_{c}+ns_{c}\mapsto e(\unicode[STIX]{x1D709}_{c}n^{2})$
from the previous example), such that
 $$\begin{eqnarray}|\mathbb{E}_{a\in P_{c,i}}f_{2}(b_{c,i})e(-\unicode[STIX]{x1D719}_{c,i}(a))|\gg 1\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}_{a\in P_{c,i}}f_{2}(b_{c,i})e(-\unicode[STIX]{x1D719}_{c,i}(a))|\gg 1\end{eqnarray}$$
for a significant fraction of the
![]() $c,i$
. Using this, one can again obtain an energy decrement of the form (3.19), where now
$c,i$
. Using this, one can again obtain an energy decrement of the form (3.19), where now
![]() $g$
is (the real part of) a scalar multiple of the functions
$g$
is (the real part of) a scalar multiple of the functions
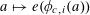 $a\mapsto e(\unicode[STIX]{x1D719}_{c,i}(a))$
on each
$a\mapsto e(\unicode[STIX]{x1D719}_{c,i}(a))$
on each
![]() $P_{c,i}$
. By arguing as in the sixth example, one can then modify
$P_{c,i}$
. By arguing as in the sixth example, one can then modify
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
in such a way that the “energy”
$f_{2}$
in such a way that the “energy”
![]() $\mathbb{E}f_{2}(\mathbf{a})^{2}$
decreases significantly, while
$\mathbb{E}f_{2}(\mathbf{a})^{2}$
decreases significantly, while
![]() $f_{1}$
is now locally quadratically structured on a somewhat finer partition of
$f_{1}$
is now locally quadratically structured on a somewhat finer partition of
![]() $\mathbb{Z}/p\mathbb{Z}$
than the original partition
$\mathbb{Z}/p\mathbb{Z}$
than the original partition
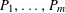 $P_{1},\ldots ,P_{m}$
, with the number of quadratic phases needed to describe
$P_{1},\ldots ,P_{m}$
, with the number of quadratic phases needed to describe
![]() $f_{1}$
on each partition having increased by one. If the function
$f_{1}$
on each partition having increased by one. If the function
![]() $f_{2}$
is now locally Gowers uniform (with respect to a new set of random variables
$f_{2}$
is now locally Gowers uniform (with respect to a new set of random variables
![]() $\mathbf{a},\mathbf{r}$
adapted to this finer partition), and there are no non-trivial relations of the form we can now (heuristically) conclude Theorem 3.1 from the analysis of the sixth example, assuming the addition of the new quadratic phase has not introduced relations of the form (3.10). If such relations occur, though, one can hope to adapt the analysis of the fourth example to reduce the quadratic complexity of the poorly distributed cells, perhaps at the cost of further subdivision of the cells. Finally, if the new version of
$\mathbf{a},\mathbf{r}$
adapted to this finer partition), and there are no non-trivial relations of the form we can now (heuristically) conclude Theorem 3.1 from the analysis of the sixth example, assuming the addition of the new quadratic phase has not introduced relations of the form (3.10). If such relations occur, though, one can hope to adapt the analysis of the fourth example to reduce the quadratic complexity of the poorly distributed cells, perhaps at the cost of further subdivision of the cells. Finally, if the new version of
![]() $f_{2}$
remains non-uniform with respect to the finer partition, then one iterates the analysis of this example to reduce the energy of
$f_{2}$
remains non-uniform with respect to the finer partition, then one iterates the analysis of this example to reduce the energy of
![]() $f_{2}$
further. This process cannot continue indefinitely due to the non-negativity of the energy (and also because none of the other steps in the iteration will cause a significant increase in energy). Because of this, one can hope to cover all cases of Theorem 3.1 by some complicated iteration of the eight arguments described above.
$f_{2}$
further. This process cannot continue indefinitely due to the non-negativity of the energy (and also because none of the other steps in the iteration will cause a significant increase in energy). Because of this, one can hope to cover all cases of Theorem 3.1 by some complicated iteration of the eight arguments described above.
Having informally discussed the eight key examples for Theorem 3.1, we return now to the task of proving this theorem rigorously.
It will be convenient to work throughout the rest of the paper with a fixed choice
 $$\begin{eqnarray}1<C_{1}<C_{2}<\cdots <C_{5}\end{eqnarray}$$
$$\begin{eqnarray}1<C_{1}<C_{2}<\cdots <C_{5}\end{eqnarray}$$
of absolute constants, with each
![]() $C_{i}$
assumed to be sufficiently large depending on the previous
$C_{i}$
assumed to be sufficiently large depending on the previous
 $C_{1},\ldots ,C_{i-1}$
. For instance, for sake of concreteness one could choose
$C_{1},\ldots ,C_{i-1}$
. For instance, for sake of concreteness one could choose
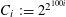 $C_{i}:=2^{2^{100i}}$
; of course, other choices are possible. The implied constants in the
$C_{i}:=2^{2^{100i}}$
; of course, other choices are possible. The implied constants in the
![]() $O(\,)$
notation will not depend on the
$O(\,)$
notation will not depend on the
![]() $C_{i}$
unless otherwise specified. These constants will serve as exponents for various scales
$C_{i}$
unless otherwise specified. These constants will serve as exponents for various scales
![]() $\unicode[STIX]{x1D702}^{-C_{i}}$
that will appear in our analysis, with the point being that any scale of the form
$\unicode[STIX]{x1D702}^{-C_{i}}$
that will appear in our analysis, with the point being that any scale of the form
![]() $\unicode[STIX]{x1D702}^{-C_{i}}$
for
$\unicode[STIX]{x1D702}^{-C_{i}}$
for
 $i=2,\ldots ,5$
is extremely tiny with respect to any polynomial combination of the previous scales
$i=2,\ldots ,5$
is extremely tiny with respect to any polynomial combination of the previous scales
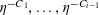 $\unicode[STIX]{x1D702}^{-C_{1}},\ldots ,\unicode[STIX]{x1D702}^{-C_{i-1}}$
.
$\unicode[STIX]{x1D702}^{-C_{1}},\ldots ,\unicode[STIX]{x1D702}^{-C_{i-1}}$
.
In all of the eight examples considered above, the function
![]() $f$
was approximated by some “quadratically structured” function, usually denoted
$f$
was approximated by some “quadratically structured” function, usually denoted
![]() $f_{1}$
, with the approximation being accurate in various senses with respect to some pair
$f_{1}$
, with the approximation being accurate in various senses with respect to some pair
![]() $(\mathbf{a},\mathbf{r})$
of random variables. The rigorous argument will similarly approximate
$(\mathbf{a},\mathbf{r})$
of random variables. The rigorous argument will similarly approximate
![]() $f$
by a quadratically structured object; it will be convenient to make this object a random function
$f$
by a quadratically structured object; it will be convenient to make this object a random function
![]() $\mathbf{f}$
rather than a deterministic one (though as it turns out, this function will become deterministic again once an auxiliary random variable
$\mathbf{f}$
rather than a deterministic one (though as it turns out, this function will become deterministic again once an auxiliary random variable
![]() $\mathbf{c}$
is fixed). The precise definition of “quadratically structured” will be rather technical, and will eventually be given in Definition 6.1. For now, we shall abstract the properties of “quadratic structure” that we will need, in the following proposition involving an abstract directed graph
$\mathbf{c}$
is fixed). The precise definition of “quadratically structured” will be rather technical, and will eventually be given in Definition 6.1. For now, we shall abstract the properties of “quadratic structure” that we will need, in the following proposition involving an abstract directed graph
 $G=(V,E)$
(encoding the “structured local approximants”), which we will construct more explicitly later. We will shortly iterate this proposition to establish Theorem 3.1 and hence Theorem 1.1.
$G=(V,E)$
(encoding the “structured local approximants”), which we will construct more explicitly later. We will shortly iterate this proposition to establish Theorem 3.1 and hence Theorem 1.1.
Proposition 3.3 (Main proposition, abstract form).
Let
![]() $\unicode[STIX]{x1D702}$
be a real number with
$\unicode[STIX]{x1D702}$
be a real number with
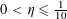 $0<\unicode[STIX]{x1D702}\leqslant {\textstyle \frac{1}{10}}$
, and let
$0<\unicode[STIX]{x1D702}\leqslant {\textstyle \frac{1}{10}}$
, and let
![]() $p$
be a prime with
$p$
be a prime with
 $$\begin{eqnarray}p\geqslant \exp (\unicode[STIX]{x1D702}^{-3C_{5}}).\end{eqnarray}$$
$$\begin{eqnarray}p\geqslant \exp (\unicode[STIX]{x1D702}^{-3C_{5}}).\end{eqnarray}$$
Let
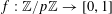 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow [0,1]$
be a function. Then there exist the following:
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow [0,1]$
be a function. Then there exist the following:
-
(a) a (possibly infinite) directed graph
 $G=(V,E)$
, with elements
$G=(V,E)$
, with elements
 $v\in V$
referred to as structured local approximants, and the notation
$v\in V$
referred to as structured local approximants, and the notation
 $v\rightarrow v^{\prime }$
used to denote the existence of a directed edge from one structured local approximant
$v\rightarrow v^{\prime }$
used to denote the existence of a directed edge from one structured local approximant
 $v$
to another
$v$
to another
 $v^{\prime }$
;
$v^{\prime }$
; -
(b) a triple
 $(\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v})$
associated to
$(\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v})$
associated to
 $f$
and to each structured local approximant
$f$
and to each structured local approximant
 $v\in V$
, where
$v\in V$
, where
 $\mathbf{a}_{v},\mathbf{r}_{v}$
are random variables in
$\mathbf{a}_{v},\mathbf{r}_{v}$
are random variables in
 $\mathbb{Z}/p\mathbb{Z}$
, and
$\mathbb{Z}/p\mathbb{Z}$
, and
 $\mathbf{f}_{v}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
is a random function (with
$\mathbf{f}_{v}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
is a random function (with
 $\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v}$
not assumed to be independent);
$\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v}$
not assumed to be independent); -
(c) a quadratic dimension
 $d_{2}(v)\in \mathbb{N}$
assigned to each vertex
$d_{2}(v)\in \mathbb{N}$
assigned to each vertex
 $v\in V$
;
$v\in V$
; -
(d) a poorly distributed quadratic dimension
 $d_{2}^{\text{poor}}(v)\in \mathbb{N}$
assigned to each vertex
$d_{2}^{\text{poor}}(v)\in \mathbb{N}$
assigned to each vertex
 $v\in V$
, with
$v\in V$
, with
 $0\leqslant d_{2}^{\text{poor}}(v)\leqslant d_{2}(v)$
; and
$0\leqslant d_{2}^{\text{poor}}(v)\leqslant d_{2}(v)$
; and -
(e) an initial approximant
 $v_{0}\in V$
, with
$v_{0}\in V$
, with
 $d_{2}(v_{0})=0$
(and hence
$d_{2}(v_{0})=0$
(and hence
 $d_{2}^{\text{poor}}(v_{0})=0$
).
$d_{2}^{\text{poor}}(v_{0})=0$
).
Furthermore, whenever a structured local approximant
![]() $v_{k}\in V$
can be reached from
$v_{k}\in V$
can be reached from
![]() $v_{0}$
by a path
$v_{0}$
by a path
 $v_{0}\rightarrow v_{1}\rightarrow \cdots \rightarrow v_{k}$
with
$v_{0}\rightarrow v_{1}\rightarrow \cdots \rightarrow v_{k}$
with
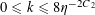 $0\leqslant k\leqslant 8\unicode[STIX]{x1D702}^{-2C_{2}}$
, then the following properties are obeyed:
$0\leqslant k\leqslant 8\unicode[STIX]{x1D702}^{-2C_{2}}$
, then the following properties are obeyed:
-
(i) one has the “thickness” condition
(3.22) $$\begin{eqnarray}\mathbb{P}(\mathbf{r}_{v_{k}}=0)\ll \exp (3\unicode[STIX]{x1D702}^{-C_{5}})/p;\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{r}_{v_{k}}=0)\ll \exp (3\unicode[STIX]{x1D702}^{-C_{5}})/p;\end{eqnarray}$$
-
(ii) we have the almost uniformity condition
(3.23) $$\begin{eqnarray}|\mathbb{E}f(\mathbf{a}_{v_{k}})-\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}f(a)|\leqslant \unicode[STIX]{x1D702};\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f(\mathbf{a}_{v_{k}})-\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}f(a)|\leqslant \unicode[STIX]{x1D702};\end{eqnarray}$$
-
(iii) bad approximation implies energy decrement: if
(3.24)or $$\begin{eqnarray}|\mathbb{E}\mathbf{f}_{v_{k}}(\mathbf{a}_{v_{k}})-f(\mathbf{a}_{v_{k}})|>\unicode[STIX]{x1D702}\end{eqnarray}$$
(3.25)then there exists a structured local approximant
$$\begin{eqnarray}|\mathbb{E}\mathbf{f}_{v_{k}}(\mathbf{a}_{v_{k}})-f(\mathbf{a}_{v_{k}})|>\unicode[STIX]{x1D702}\end{eqnarray}$$
(3.25)then there exists a structured local approximant $$\begin{eqnarray}|\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(\mathbf{f}_{v_{k}})-\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(f)|>\unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(\mathbf{f}_{v_{k}})-\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(f)|>\unicode[STIX]{x1D702}\end{eqnarray}$$
 $v_{k+1}\in V$
with
$v_{k+1}\in V$
with
 $v_{k}\rightarrow v_{k+1}$
such that and
$v_{k}\rightarrow v_{k+1}$
such that and $$\begin{eqnarray}\mathbb{E}|f(\mathbf{a}_{v_{k+1}})-\mathbf{f}_{v_{k+1}}(\mathbf{a}_{v_{k+1}})|^{2}\leqslant \mathbb{E}|f(\mathbf{a}_{v_{k}})-\mathbf{f}_{v_{k}}k(\mathbf{a}_{v_{k}})|^{2}-\unicode[STIX]{x1D702}^{C_{2}}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}|f(\mathbf{a}_{v_{k+1}})-\mathbf{f}_{v_{k+1}}(\mathbf{a}_{v_{k+1}})|^{2}\leqslant \mathbb{E}|f(\mathbf{a}_{v_{k}})-\mathbf{f}_{v_{k}}k(\mathbf{a}_{v_{k}})|^{2}-\unicode[STIX]{x1D702}^{C_{2}}\end{eqnarray}$$
 $$\begin{eqnarray}d_{2}(v_{k+1})\leqslant d_{2}(v_{k})+1.\end{eqnarray}$$
$$\begin{eqnarray}d_{2}(v_{k+1})\leqslant d_{2}(v_{k})+1.\end{eqnarray}$$
-
(iv) failure of “Khinchin-type recurrence” implies dimension decrement: if
(3.26)then there exists a structured local approximant $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(\mathbf{f}_{v_{k}})\leqslant (\mathbb{E}\mathbf{f}_{v_{k}}(\mathbf{a}_{v_{k}}))^{4}-\unicode[STIX]{x1D702},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(\mathbf{f}_{v_{k}})\leqslant (\mathbb{E}\mathbf{f}_{v_{k}}(\mathbf{a}_{v_{k}}))^{4}-\unicode[STIX]{x1D702},\end{eqnarray}$$
 $v_{k+1}\in V$
with
$v_{k+1}\in V$
with
 $v_{k}\rightarrow v_{k+1}$
obeying the bounds
$v_{k}\rightarrow v_{k+1}$
obeying the bounds  $$\begin{eqnarray}\displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k+1}})-\mathbf{f}_{v_{k+1}}(\mathbf{a}_{v_{k+1}})|^{2} & {\leqslant} & \displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k}})-\mathbf{f}_{v_{k}}(\mathbf{a}_{v_{k}})|^{2}+\unicode[STIX]{x1D702}^{3C_{2}},\nonumber\\ \displaystyle d_{2}(v_{k+1}) & {\leqslant} & \displaystyle d_{2}(v_{k}),\nonumber\\ \displaystyle d_{2}^{\text{poor}}(v_{k+1}) & {\leqslant} & \displaystyle d_{2}^{\text{poor}}(v_{k})-1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k+1}})-\mathbf{f}_{v_{k+1}}(\mathbf{a}_{v_{k+1}})|^{2} & {\leqslant} & \displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k}})-\mathbf{f}_{v_{k}}(\mathbf{a}_{v_{k}})|^{2}+\unicode[STIX]{x1D702}^{3C_{2}},\nonumber\\ \displaystyle d_{2}(v_{k+1}) & {\leqslant} & \displaystyle d_{2}(v_{k}),\nonumber\\ \displaystyle d_{2}^{\text{poor}}(v_{k+1}) & {\leqslant} & \displaystyle d_{2}^{\text{poor}}(v_{k})-1.\nonumber\end{eqnarray}$$
The proof of this proposition will occupy the remainder of the paper. For now, let us see how this proposition implies Theorem 3.1. Let
![]() $p,\unicode[STIX]{x1D702},f$
be as in that theorem, and let
$p,\unicode[STIX]{x1D702},f$
be as in that theorem, and let
 $C_{1},\ldots ,C_{5}$
be as above. If the largeness criterion (3.21) fails, then we may set
$C_{1},\ldots ,C_{5}$
be as above. If the largeness criterion (3.21) fails, then we may set
![]() $\mathbf{r}:=0$
,
$\mathbf{r}:=0$
,
![]() $\mathbf{f}:=f$
, and draw
$\mathbf{f}:=f$
, and draw
![]() $\mathbf{a}$
uniformly at random from
$\mathbf{a}$
uniformly at random from
![]() $\mathbb{Z}/p\mathbb{Z}$
, and it is easy to see that the conclusions of Theorem 3.1 are obeyed (with (3.3) following from Hölder’s inequality). Thus we may assume without loss of generality that (3.21) holds.
$\mathbb{Z}/p\mathbb{Z}$
, and it is easy to see that the conclusions of Theorem 3.1 are obeyed (with (3.3) following from Hölder’s inequality). Thus we may assume without loss of generality that (3.21) holds.
Let
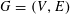 $G=(V,E)$
,
$G=(V,E)$
,
![]() $v_{0}$
,
$v_{0}$
,
![]() $d_{2}(\,)$
,
$d_{2}(\,)$
,
![]() $d_{2}^{\text{poor}}(\,)$
, and
$d_{2}^{\text{poor}}(\,)$
, and
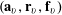 $(\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v})$
be as in Proposition 3.3. Suppose first that there exists a structured local approximant
$(\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v})$
be as in Proposition 3.3. Suppose first that there exists a structured local approximant
![]() $v_{k}\in V$
that can be reached from
$v_{k}\in V$
that can be reached from
![]() $v_{0}$
by a path of length at most
$v_{0}$
by a path of length at most
![]() $8\unicode[STIX]{x1D702}^{-2C_{2}}$
, and for which none of the inequalities (3.24)–(3.26) hold, that is to say one has the bounds
$8\unicode[STIX]{x1D702}^{-2C_{2}}$
, and for which none of the inequalities (3.24)–(3.26) hold, that is to say one has the bounds
 $$\begin{eqnarray}\displaystyle & \displaystyle |\mathbb{E}\mathbf{f}_{v_{k}}(\mathbf{a}_{v_{k}})-f_{v_{k}}(\mathbf{a}_{v_{k}})|\leqslant \unicode[STIX]{x1D702}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle |\mathbb{E}\mathbf{f}_{v_{k}}(\mathbf{a}_{v_{k}})-f_{v_{k}}(\mathbf{a}_{v_{k}})|\leqslant \unicode[STIX]{x1D702}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle |\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(\mathbf{f}_{v_{k}})-\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(f_{v_{k}})|\leqslant \unicode[STIX]{x1D702} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle |\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(\mathbf{f}_{v_{k}})-\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(f_{v_{k}})|\leqslant \unicode[STIX]{x1D702} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(\mathbf{f}_{v_{k}})>(\mathbb{E}\mathbf{f}_{v_{k}}(\mathbf{a}_{v_{k}}))^{4}-\unicode[STIX]{x1D702}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(\mathbf{f}_{v_{k}})>(\mathbb{E}\mathbf{f}_{v_{k}}(\mathbf{a}_{v_{k}}))^{4}-\unicode[STIX]{x1D702}. & \displaystyle\end{eqnarray}$$
From (3.29), (3.28), (3.27) and the triangle inequality (and the boundedness of
![]() $\mathbf{f}_{v_{k}},f$
) we conclude that
$\mathbf{f}_{v_{k}},f$
) we conclude that
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(f_{v_{k}})>(\mathbb{E}f(\mathbf{a}_{v_{k}}))^{4}-O(\unicode[STIX]{x1D702});\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}}(f_{v_{k}})>(\mathbb{E}f(\mathbf{a}_{v_{k}}))^{4}-O(\unicode[STIX]{x1D702});\end{eqnarray}$$
combining this with (3.22) and (3.23) we see that the random variables
![]() $\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}$
obey the properties required of Theorem 3.1. Thus we may assume for sake of contradiction that this situation never occurs, which by Proposition 3.3 implies that whenever
$\mathbf{a}_{v_{k}},\mathbf{r}_{v_{k}}$
obey the properties required of Theorem 3.1. Thus we may assume for sake of contradiction that this situation never occurs, which by Proposition 3.3 implies that whenever
![]() $v_{k}\in V$
is a structured local approximant that can be reached from
$v_{k}\in V$
is a structured local approximant that can be reached from
![]() $v_{0}$
by a path of length at most
$v_{0}$
by a path of length at most
![]() $8\unicode[STIX]{x1D702}^{-2C_{2}}$
, then the conclusions of at least one of (iii) and (iv) hold. Iterating this we may therefore construct a path
$8\unicode[STIX]{x1D702}^{-2C_{2}}$
, then the conclusions of at least one of (iii) and (iv) hold. Iterating this we may therefore construct a path
 $$\begin{eqnarray}v_{0}\rightarrow v_{1}\rightarrow \cdots \rightarrow v_{k_{0}+1}\end{eqnarray}$$
$$\begin{eqnarray}v_{0}\rightarrow v_{1}\rightarrow \cdots \rightarrow v_{k_{0}+1}\end{eqnarray}$$
with
 $$\begin{eqnarray}k_{0}:=\lfloor 8\unicode[STIX]{x1D702}^{-2C_{2}}\rfloor ,\end{eqnarray}$$
$$\begin{eqnarray}k_{0}:=\lfloor 8\unicode[STIX]{x1D702}^{-2C_{2}}\rfloor ,\end{eqnarray}$$
such that for every
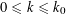 $0\leqslant k\leqslant k_{0}$
, one either has the energy decrement bounds
$0\leqslant k\leqslant k_{0}$
, one either has the energy decrement bounds
 $$\begin{eqnarray}\displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k+1}})-\mathbf{f}_{k+1}(\mathbf{a}_{v_{k+1}})|^{2} & {\leqslant} & \displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k}})-\mathbf{f}_{k}(\mathbf{a}_{v_{k}})|^{2}-\unicode[STIX]{x1D702}^{C_{2}},\nonumber\\ \displaystyle d_{2}(v_{k+1}) & {\leqslant} & \displaystyle d_{2}(v_{k})+1\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k+1}})-\mathbf{f}_{k+1}(\mathbf{a}_{v_{k+1}})|^{2} & {\leqslant} & \displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k}})-\mathbf{f}_{k}(\mathbf{a}_{v_{k}})|^{2}-\unicode[STIX]{x1D702}^{C_{2}},\nonumber\\ \displaystyle d_{2}(v_{k+1}) & {\leqslant} & \displaystyle d_{2}(v_{k})+1\nonumber\end{eqnarray}$$
or the dimension decrement bounds
 $$\begin{eqnarray}\displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k+1}})-\mathbf{f}_{k+1}(\mathbf{a}_{v_{k+1}})|^{2} & {\leqslant} & \displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k}})-\mathbf{f}_{k}(\mathbf{a}_{v_{k}})|^{2}+\unicode[STIX]{x1D702}^{3C_{2}},\nonumber\\ \displaystyle d_{2}(v_{k+1}) & {\leqslant} & \displaystyle d_{2}(v_{k}),\nonumber\\ \displaystyle d_{2}^{\text{poor}}(v_{k+1}) & {\leqslant} & \displaystyle d_{2}^{\text{poor}}(v_{k})-1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k+1}})-\mathbf{f}_{k+1}(\mathbf{a}_{v_{k+1}})|^{2} & {\leqslant} & \displaystyle \mathbb{E}|f(\mathbf{a}_{v_{k}})-\mathbf{f}_{k}(\mathbf{a}_{v_{k}})|^{2}+\unicode[STIX]{x1D702}^{3C_{2}},\nonumber\\ \displaystyle d_{2}(v_{k+1}) & {\leqslant} & \displaystyle d_{2}(v_{k}),\nonumber\\ \displaystyle d_{2}^{\text{poor}}(v_{k+1}) & {\leqslant} & \displaystyle d_{2}^{\text{poor}}(v_{k})-1.\nonumber\end{eqnarray}$$
Since
![]() $v_{0}$
already has the minimum quadratic dimension
$v_{0}$
already has the minimum quadratic dimension
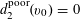 $d_{2}^{\text{poor}}(v_{0})=0$
, we see that we must experience an energy decrement at the
$d_{2}^{\text{poor}}(v_{0})=0$
, we see that we must experience an energy decrement at the
![]() $k=0$
stage. Also, if
$k=0$
stage. Also, if
![]() $k$
is the
$k$
is the
![]() $j$
th index to experience an energy decrement, we see that
$j$
th index to experience an energy decrement, we see that
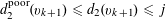 $d_{2}^{\text{poor}}(v_{k+1})\leqslant d_{2}(v_{k+1})\leqslant j$
, and so one can have at most
$d_{2}^{\text{poor}}(v_{k+1})\leqslant d_{2}(v_{k+1})\leqslant j$
, and so one can have at most
![]() $j$
consecutive dimension decrements after the
$j$
consecutive dimension decrements after the
![]() $k$
th stage; in other words, we must experience another energy decrement within
$k$
th stage; in other words, we must experience another energy decrement within
![]() $j+1$
steps. By definition of
$j+1$
steps. By definition of
![]() $k_{0}$
, we have
$k_{0}$
, we have
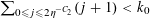 $\sum _{0\leqslant j\leqslant 2\unicode[STIX]{x1D702}^{-C_{2}}}(j+1)<k_{0}$
if
$\sum _{0\leqslant j\leqslant 2\unicode[STIX]{x1D702}^{-C_{2}}}(j+1)<k_{0}$
if
![]() $C_{2}$
is large enough. We conclude that at least
$C_{2}$
is large enough. We conclude that at least
![]() $2\unicode[STIX]{x1D702}^{-C_{2}}$
energy decrements occur within the path
$2\unicode[STIX]{x1D702}^{-C_{2}}$
energy decrements occur within the path
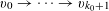 $v_{0}\rightarrow \cdots \rightarrow v_{k_{0}+1}$
. This implies that
$v_{0}\rightarrow \cdots \rightarrow v_{k_{0}+1}$
. This implies that
 $$\begin{eqnarray}\mathbb{E}|f(\mathbf{a}_{v_{k_{0}+1}})-\mathbf{f}_{k_{0}+1}(\mathbf{a}_{v_{k_{0}+1}})|^{2}\leqslant \mathbb{E}|f(\mathbf{a}_{v_{0}})-\mathbf{f}_{k+1}(\mathbf{a}_{v_{0}})|^{2}-(2\unicode[STIX]{x1D702}^{-C_{2}})\unicode[STIX]{x1D702}^{C_{2}}+k_{0}\unicode[STIX]{x1D702}^{3C_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}|f(\mathbf{a}_{v_{k_{0}+1}})-\mathbf{f}_{k_{0}+1}(\mathbf{a}_{v_{k_{0}+1}})|^{2}\leqslant \mathbb{E}|f(\mathbf{a}_{v_{0}})-\mathbf{f}_{k+1}(\mathbf{a}_{v_{0}})|^{2}-(2\unicode[STIX]{x1D702}^{-C_{2}})\unicode[STIX]{x1D702}^{C_{2}}+k_{0}\unicode[STIX]{x1D702}^{3C_{2}}.\end{eqnarray}$$
But if
![]() $C_{2}$
is sufficiently large, this implies from (3.30) that
$C_{2}$
is sufficiently large, this implies from (3.30) that
 $$\begin{eqnarray}\mathbb{E}|f(\mathbf{a}_{v_{k_{0}+1}})-\mathbf{f}_{k_{0}+1}(\mathbf{a}_{v_{k_{0}+1}})|^{2}<\mathbb{E}|f(\mathbf{a}_{v_{0}})-\mathbf{f}_{0}(\mathbf{a}_{v_{0}})|^{2}-4\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}|f(\mathbf{a}_{v_{k_{0}+1}})-\mathbf{f}_{k_{0}+1}(\mathbf{a}_{v_{k_{0}+1}})|^{2}<\mathbb{E}|f(\mathbf{a}_{v_{0}})-\mathbf{f}_{0}(\mathbf{a}_{v_{0}})|^{2}-4\end{eqnarray}$$
(for example), which leads to a contradiction because the left-hand side is clearly non-negative, and the right-hand side non-positive. This gives the desired contradiction that establishes Theorem 3.1 and hence Theorem 1.1.
It remains to establish Proposition 3.3. This will occupy the remaining portions of the paper.
4 Bohr sets
To define and manipulate the “structured local approximants” that appear in Proposition 3.3, we will need to develop the theory of two mathematical objects. The first is that of a Bohr set, which will be covered in this section; the second is that of a dilated torus, which we will discuss in the next section.
Definition 4.1 (Bohr set).
A subset
![]() $S$
of
$S$
of
![]() $\mathbb{Z}/p\mathbb{Z}$
is said to be non-degenerate if it contains at least one non-zero element. In this case we define the dual
$\mathbb{Z}/p\mathbb{Z}$
is said to be non-degenerate if it contains at least one non-zero element. In this case we define the dual
![]() $S$
-norm
$S$
-norm
 $$\begin{eqnarray}\Vert a\Vert _{S^{\bot }}:=\sup _{\unicode[STIX]{x1D709}\in S}\biggl\|\frac{a\unicode[STIX]{x1D709}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert a\Vert _{S^{\bot }}:=\sup _{\unicode[STIX]{x1D709}\in S}\biggl\|\frac{a\unicode[STIX]{x1D709}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\end{eqnarray}$$
for any
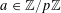 $a\in \mathbb{Z}/p\mathbb{Z}$
, and then define the Bohr set
$a\in \mathbb{Z}/p\mathbb{Z}$
, and then define the Bohr set
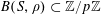 $B(S,\unicode[STIX]{x1D70C})\subset \mathbb{Z}/p\mathbb{Z}$
for any
$B(S,\unicode[STIX]{x1D70C})\subset \mathbb{Z}/p\mathbb{Z}$
for any
![]() $\unicode[STIX]{x1D70C}>0$
by the formula
$\unicode[STIX]{x1D70C}>0$
by the formula
 $$\begin{eqnarray}B(S,\unicode[STIX]{x1D70C}):=\{a\in \mathbb{Z}/p\mathbb{Z}:\Vert a\Vert _{S^{\bot }}<\unicode[STIX]{x1D70C}\}\end{eqnarray}$$
$$\begin{eqnarray}B(S,\unicode[STIX]{x1D70C}):=\{a\in \mathbb{Z}/p\mathbb{Z}:\Vert a\Vert _{S^{\bot }}<\unicode[STIX]{x1D70C}\}\end{eqnarray}$$
where
![]() $\Vert \unicode[STIX]{x1D703}\Vert _{\mathbb{R}/\mathbb{Z}}$
denotes the distance from
$\Vert \unicode[STIX]{x1D703}\Vert _{\mathbb{R}/\mathbb{Z}}$
denotes the distance from
![]() $\unicode[STIX]{x1D703}$
to the nearest integer. We refer to
$\unicode[STIX]{x1D703}$
to the nearest integer. We refer to
![]() $S$
as the set of frequencies of the Bohr set,
$S$
as the set of frequencies of the Bohr set,
![]() $\unicode[STIX]{x1D70C}$
as the radius, and
$\unicode[STIX]{x1D70C}$
as the radius, and
![]() $|S|$
as the rank of the Bohr set. We also define the shifted Bohr sets
$|S|$
as the rank of the Bohr set. We also define the shifted Bohr sets
 $$\begin{eqnarray}n+B(S,\unicode[STIX]{x1D70C}):=\{a+n:a\in B(S,\unicode[STIX]{x1D70C})\}\end{eqnarray}$$
$$\begin{eqnarray}n+B(S,\unicode[STIX]{x1D70C}):=\{a+n:a\in B(S,\unicode[STIX]{x1D70C})\}\end{eqnarray}$$
for any
 $n\in \mathbb{Z}/p\mathbb{Z}$
.
$n\in \mathbb{Z}/p\mathbb{Z}$
.
From (2.4) we have the triangle inequalities
 $$\begin{eqnarray}\Vert a+b\Vert _{S^{\bot }}\leqslant \Vert a\Vert _{S^{\bot }}+\Vert b\Vert _{S^{\bot }};\qquad \Vert ka\Vert _{S^{\bot }}\leqslant |k|\Vert a\Vert _{S^{\bot }}\end{eqnarray}$$
$$\begin{eqnarray}\Vert a+b\Vert _{S^{\bot }}\leqslant \Vert a\Vert _{S^{\bot }}+\Vert b\Vert _{S^{\bot }};\qquad \Vert ka\Vert _{S^{\bot }}\leqslant |k|\Vert a\Vert _{S^{\bot }}\end{eqnarray}$$
for
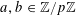 $a,b\in \mathbb{Z}/p\mathbb{Z}$
and
$a,b\in \mathbb{Z}/p\mathbb{Z}$
and
![]() $k\in \mathbb{Z}$
; also we trivially have
$k\in \mathbb{Z}$
; also we trivially have
 $$\begin{eqnarray}\Vert a\Vert _{S^{\bot }}\leqslant \Vert a\Vert _{(S^{\prime })^{\bot }}\end{eqnarray}$$
$$\begin{eqnarray}\Vert a\Vert _{S^{\bot }}\leqslant \Vert a\Vert _{(S^{\prime })^{\bot }}\end{eqnarray}$$
if
![]() $S\subset S^{\prime }$
and
$S\subset S^{\prime }$
and
 $a\in \mathbb{Z}/p\mathbb{Z}$
, or equivalently that
$a\in \mathbb{Z}/p\mathbb{Z}$
, or equivalently that
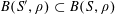 $B(S^{\prime },\unicode[STIX]{x1D70C})\subset B(S,\unicode[STIX]{x1D70C})$
for
$B(S^{\prime },\unicode[STIX]{x1D70C})\subset B(S,\unicode[STIX]{x1D70C})$
for
![]() $\unicode[STIX]{x1D70C}>0$
. We will frequently use these inequalities in the sequel, usually without further comment. In Lemma 4.6 below, we will show that
$\unicode[STIX]{x1D70C}>0$
. We will frequently use these inequalities in the sequel, usually without further comment. In Lemma 4.6 below, we will show that
![]() $\Vert \Vert _{S^{\bot }}$
is “dual” to a certain word norm
$\Vert \Vert _{S^{\bot }}$
is “dual” to a certain word norm
![]() $\Vert \Vert _{S}$
on
$\Vert \Vert _{S}$
on
![]() $\mathbb{Z}/p\mathbb{Z}$
. One could also define Bohr sets in the case when
$\mathbb{Z}/p\mathbb{Z}$
. One could also define Bohr sets in the case when
![]() $S$
is degenerate, but this creates some minor complications in our arguments, so we remove this case from our definition of a Bohr set.
$S$
is degenerate, but this creates some minor complications in our arguments, so we remove this case from our definition of a Bohr set.
We have the following standard size bounds for Bohr sets, whose proof may be found in [Reference Tao and Vu33, Lemma 4.20].
Lemma 4.2. If
![]() $B(S,\unicode[STIX]{x1D70C})$
is a Bohr set, then
$B(S,\unicode[STIX]{x1D70C})$
is a Bohr set, then
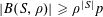 $|B(S,\unicode[STIX]{x1D70C})|\geqslant \unicode[STIX]{x1D70C}^{|S|}p$
and
$|B(S,\unicode[STIX]{x1D70C})|\geqslant \unicode[STIX]{x1D70C}^{|S|}p$
and
 $|B(S,2\unicode[STIX]{x1D70C})|\leqslant 4^{|S|}|B(S,\unicode[STIX]{x1D70C})|$
.
$|B(S,2\unicode[STIX]{x1D70C})|\leqslant 4^{|S|}|B(S,\unicode[STIX]{x1D70C})|$
.
In previous work on Roth-type theorems, one sometimes restricts attention to regular Bohr sets, as first introduced in [Reference Bourgain6]; see [Reference Tao and Vu33, §4.4] for some discussion of this concept. Due to our use of the probabilistic method, we will be able to work with a technically simpler and “smoothed out” version of a regular Bohr set, which we call the regular probability distribution on a Bohr set.
Definition 4.3. Let
![]() $B(S,\unicode[STIX]{x1D70C})$
be a Bohr set. The regular probability distribution
$B(S,\unicode[STIX]{x1D70C})$
be a Bohr set. The regular probability distribution
 $\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C})}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{R}$
associated to
$\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C})}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{R}$
associated to
![]() $B(S,\unicode[STIX]{x1D70C})$
is the function defined by the formula
$B(S,\unicode[STIX]{x1D70C})$
is the function defined by the formula
 $$\begin{eqnarray}\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C})}(a):=2\int _{1/2}^{1}\frac{1_{B(S,t\unicode[STIX]{x1D70C})}(a)}{|B(S,t\unicode[STIX]{x1D70C})|}\,dt;\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C})}(a):=2\int _{1/2}^{1}\frac{1_{B(S,t\unicode[STIX]{x1D70C})}(a)}{|B(S,t\unicode[STIX]{x1D70C})|}\,dt;\end{eqnarray}$$
it is easy to see (from Fubini’s theorem) that this is indeed a probability distribution on
![]() $\mathbb{Z}/p\mathbb{Z}$
. A random variable
$\mathbb{Z}/p\mathbb{Z}$
. A random variable
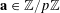 $\mathbf{a}\in \mathbb{Z}/p\mathbb{Z}$
is said to be drawn regularly from
$\mathbf{a}\in \mathbb{Z}/p\mathbb{Z}$
is said to be drawn regularly from
![]() $B(S,\unicode[STIX]{x1D70C})$
if it has probability density function
$B(S,\unicode[STIX]{x1D70C})$
if it has probability density function
![]() $\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C})}$
, thus
$\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C})}$
, thus
 $\mathbb{P}(\mathbf{a}=a)=\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C})}(a)$
for all
$\mathbb{P}(\mathbf{a}=a)=\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C})}(a)$
for all
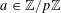 $a\in \mathbb{Z}/p\mathbb{Z}$
.
$a\in \mathbb{Z}/p\mathbb{Z}$
.
More generally, for any shifted Bohr set
 $n+B(S,\unicode[STIX]{x1D70C})$
, we define the regular probability distribution
$n+B(S,\unicode[STIX]{x1D70C})$
, we define the regular probability distribution
 $\mathfrak{p}_{n+B(S,\unicode[STIX]{x1D70C})}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{R}$
by the formula
$\mathfrak{p}_{n+B(S,\unicode[STIX]{x1D70C})}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{R}$
by the formula
 $$\begin{eqnarray}\mathfrak{p}_{n+B(S,\unicode[STIX]{x1D70C})}(a):=\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C})}(a-n),\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}_{n+B(S,\unicode[STIX]{x1D70C})}(a):=\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C})}(a-n),\end{eqnarray}$$
and say that
![]() $\mathbf{a}$
is drawn regularly from
$\mathbf{a}$
is drawn regularly from
 $n+B(S,\unicode[STIX]{x1D70C})$
if it has probability distribution
$n+B(S,\unicode[STIX]{x1D70C})$
if it has probability distribution
 $\mathfrak{p}_{n+B(S,\unicode[STIX]{x1D70C})}$
.
$\mathfrak{p}_{n+B(S,\unicode[STIX]{x1D70C})}$
.
Informally, to draw a random variable
![]() $\mathbf{a}$
regularly from
$\mathbf{a}$
regularly from
 $n+B(S,\unicode[STIX]{x1D70C})$
, one should draw it uniformly from
$n+B(S,\unicode[STIX]{x1D70C})$
, one should draw it uniformly from
 $n\,+\,B(S,\mathbf{t}\unicode[STIX]{x1D70C})$
, where
$n\,+\,B(S,\mathbf{t}\unicode[STIX]{x1D70C})$
, where
![]() $\mathbf{t}$
is itself selected uniformly at random from the interval
$\mathbf{t}$
is itself selected uniformly at random from the interval
![]() $[1/2,1]$
. Note that if
$[1/2,1]$
. Note that if
![]() $\mathbf{a}$
is drawn regularly from
$\mathbf{a}$
is drawn regularly from
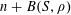 $n+B(S,\unicode[STIX]{x1D70C})$
, then
$n+B(S,\unicode[STIX]{x1D70C})$
, then
![]() $m+\mathbf{a}$
will be drawn regularly from
$m+\mathbf{a}$
will be drawn regularly from
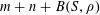 $m+n+B(S,\unicode[STIX]{x1D70C})$
for any
$m+n+B(S,\unicode[STIX]{x1D70C})$
for any
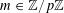 $m\in \mathbb{Z}/p\mathbb{Z}$
, and similarly
$m\in \mathbb{Z}/p\mathbb{Z}$
, and similarly
![]() $k\mathbf{a}$
will be drawn from
$k\mathbf{a}$
will be drawn from
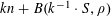 $kn+B(k^{-1}\cdot S,\unicode[STIX]{x1D70C})$
for any non-zero
$kn+B(k^{-1}\cdot S,\unicode[STIX]{x1D70C})$
for any non-zero
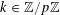 $k\in \mathbb{Z}/p\mathbb{Z}$
, where
$k\in \mathbb{Z}/p\mathbb{Z}$
, where
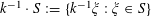 $k^{-1}\cdot S:=\{k^{-1}\unicode[STIX]{x1D709}:\unicode[STIX]{x1D709}\in S\}$
is the dilate of the frequency set
$k^{-1}\cdot S:=\{k^{-1}\unicode[STIX]{x1D709}:\unicode[STIX]{x1D709}\in S\}$
is the dilate of the frequency set
![]() $S$
by
$S$
by
![]() $k^{-1}$
.
$k^{-1}$
.
From Lemma 4.2 we see that if
![]() $\mathbf{a}$
is drawn regularly from a shifted Bohr set
$\mathbf{a}$
is drawn regularly from a shifted Bohr set
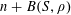 $n+B(S,\unicode[STIX]{x1D70C})$
, then
$n+B(S,\unicode[STIX]{x1D70C})$
, then
 $$\begin{eqnarray}\mathbb{P}(\mathbf{a}=a)\leqslant \frac{1}{(\unicode[STIX]{x1D70C}/2)^{|S|}p}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{a}=a)\leqslant \frac{1}{(\unicode[STIX]{x1D70C}/2)^{|S|}p}\end{eqnarray}$$
for all
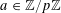 $a\in \mathbb{Z}/p\mathbb{Z}$
. In practice, this will mean that the influence of any given value of
$a\in \mathbb{Z}/p\mathbb{Z}$
. In practice, this will mean that the influence of any given value of
![]() $\mathbf{a}$
will be negligible.
$\mathbf{a}$
will be negligible.
The presence of the averaging parameter
![]() $t$
in (4.2) allows for the following very convenient approximate translation-invariance property. Given two random variables
$t$
in (4.2) allows for the following very convenient approximate translation-invariance property. Given two random variables
![]() $\mathbf{a},\mathbf{a}^{\prime }$
taking values in a finite set
$\mathbf{a},\mathbf{a}^{\prime }$
taking values in a finite set
![]() $A$
, we define the total variation distance between the two to be the quantity
$A$
, we define the total variation distance between the two to be the quantity
 $$\begin{eqnarray}d_{\operatorname{TV}}(\mathbf{a},\mathbf{a}^{\prime }):=\mathop{\sum }_{a\in A}|\mathbb{P}(\mathbf{a}=a)-\mathbb{P}(\mathbf{a}^{\prime }=a)|,\end{eqnarray}$$
$$\begin{eqnarray}d_{\operatorname{TV}}(\mathbf{a},\mathbf{a}^{\prime }):=\mathop{\sum }_{a\in A}|\mathbb{P}(\mathbf{a}=a)-\mathbb{P}(\mathbf{a}^{\prime }=a)|,\end{eqnarray}$$
or equivalently
 $$\begin{eqnarray}d_{\operatorname{TV}}(\mathbf{a},\mathbf{a}^{\prime })=\sup _{f}|\mathbb{E}f(\mathbf{a})-\mathbb{E}f(\mathbf{a}^{\prime })|\end{eqnarray}$$
$$\begin{eqnarray}d_{\operatorname{TV}}(\mathbf{a},\mathbf{a}^{\prime })=\sup _{f}|\mathbb{E}f(\mathbf{a})-\mathbb{E}f(\mathbf{a}^{\prime })|\end{eqnarray}$$
where
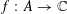 $f:A\rightarrow \mathbb{C}$
ranges over
$f:A\rightarrow \mathbb{C}$
ranges over
![]() $1$
-bounded functions.
$1$
-bounded functions.
The next lemma gives some approximate translation-invariance properties of Bohr sets. Its proof is a thinly disguised version of the arguments of Bourgain [Reference Bourgain6].
Lemma 4.4. Let
 $n+B(S,\unicode[STIX]{x1D70C})$
be a shifted Bohr set, and let
$n+B(S,\unicode[STIX]{x1D70C})$
be a shifted Bohr set, and let
![]() $\mathbf{a}$
be drawn regularly from
$\mathbf{a}$
be drawn regularly from
![]() $B(S,\unicode[STIX]{x1D70C})$
. Let
$B(S,\unicode[STIX]{x1D70C})$
. Let
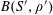 $B(S^{\prime },\unicode[STIX]{x1D70C}^{\prime })$
be another Bohr set with
$B(S^{\prime },\unicode[STIX]{x1D70C}^{\prime })$
be another Bohr set with
![]() $S^{\prime }\supset S$
.
$S^{\prime }\supset S$
.
-
(i) If
 $h\in B(S^{\prime },\unicode[STIX]{x1D70C}^{\prime })$
, then
$h\in B(S^{\prime },\unicode[STIX]{x1D70C}^{\prime })$
, then
 $\mathbf{a}$
and
$\mathbf{a}$
and
 $\mathbf{a}+h$
differ in total variation by at most
$\mathbf{a}+h$
differ in total variation by at most
 $O(|S|\unicode[STIX]{x1D70C}^{\prime }/\unicode[STIX]{x1D70C})$
.
$O(|S|\unicode[STIX]{x1D70C}^{\prime }/\unicode[STIX]{x1D70C})$
. -
(ii) More generally, if
 $\mathbf{h}$
is a random variable independent of
$\mathbf{h}$
is a random variable independent of
 $\mathbf{a}$
that takes values in
$\mathbf{a}$
that takes values in
 $B(S^{\prime },\unicode[STIX]{x1D70C}^{\prime })$
, then
$B(S^{\prime },\unicode[STIX]{x1D70C}^{\prime })$
, then
 $\mathbf{a}$
and
$\mathbf{a}$
and
 $\mathbf{a}+\mathbf{h}$
differ in total variation by at most
$\mathbf{a}+\mathbf{h}$
differ in total variation by at most
 $O(|S|\unicode[STIX]{x1D70C}^{\prime }/\unicode[STIX]{x1D70C})$
.
$O(|S|\unicode[STIX]{x1D70C}^{\prime }/\unicode[STIX]{x1D70C})$
.
Proof. To prove (i), it suffices to show that
 $$\begin{eqnarray}\mathbb{E}f(\mathbf{a}+h)=\mathbb{E}f(\mathbf{a})+O\biggl(|S|\frac{\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x1D70C}}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f(\mathbf{a}+h)=\mathbb{E}f(\mathbf{a})+O\biggl(|S|\frac{\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x1D70C}}\biggr)\end{eqnarray}$$
for any
![]() $1$
-bounded function
$1$
-bounded function
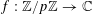 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
; the claim (ii) then also follows by conditioning
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
; the claim (ii) then also follows by conditioning
![]() $\mathbf{h}$
to a fixed value
$\mathbf{h}$
to a fixed value
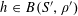 $h\in B(S^{\prime },\unicode[STIX]{x1D70C}^{\prime })$
, then multiplying by
$h\in B(S^{\prime },\unicode[STIX]{x1D70C}^{\prime })$
, then multiplying by
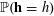 $\mathbb{P}(\mathbf{h}=h)$
and summing over
$\mathbb{P}(\mathbf{h}=h)$
and summing over
![]() $h$
.
$h$
.
By translating
![]() $f$
by
$f$
by
![]() $n$
, we may assume that
$n$
, we may assume that
![]() $n=0$
. We may assume that
$n=0$
. We may assume that
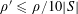 $\unicode[STIX]{x1D70C}^{\prime }\leqslant \unicode[STIX]{x1D70C}/10|S|$
, as the claim is trivial otherwise.
$\unicode[STIX]{x1D70C}^{\prime }\leqslant \unicode[STIX]{x1D70C}/10|S|$
, as the claim is trivial otherwise.
From (4.2) we have
 $$\begin{eqnarray}\mathbb{E}f(\mathbf{a})=2\int _{1/2}^{1}\mathop{\sum }_{a\in \mathbb{Z}/p\mathbb{Z}}f(a)\frac{1_{B(S,t\unicode[STIX]{x1D70C})}(a)}{|B(S,t\unicode[STIX]{x1D70C})|}\,dt\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f(\mathbf{a})=2\int _{1/2}^{1}\mathop{\sum }_{a\in \mathbb{Z}/p\mathbb{Z}}f(a)\frac{1_{B(S,t\unicode[STIX]{x1D70C})}(a)}{|B(S,t\unicode[STIX]{x1D70C})|}\,dt\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathbb{E}f(\mathbf{a}+h)=2\int _{1/2}^{1}\mathop{\sum }_{a\in \mathbb{Z}/p\mathbb{Z}}f(a)\frac{1_{B(S,t\unicode[STIX]{x1D70C})-h}(a)}{|B(S,t\unicode[STIX]{x1D70C})|}\,dt\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f(\mathbf{a}+h)=2\int _{1/2}^{1}\mathop{\sum }_{a\in \mathbb{Z}/p\mathbb{Z}}f(a)\frac{1_{B(S,t\unicode[STIX]{x1D70C})-h}(a)}{|B(S,t\unicode[STIX]{x1D70C})|}\,dt\end{eqnarray}$$
so by the triangle inequality it suffices to show that
 $$\begin{eqnarray}\int _{1/2}^{1}\frac{\mathop{\sum }_{a\in \mathbb{Z}/p\mathbb{Z}}|1_{B(S,t\unicode[STIX]{x1D70C})}(a)-1_{B(S,t\unicode[STIX]{x1D70C})-h}(a)|}{|B(S,t\unicode[STIX]{x1D70C})|}\,dt\ll |S|\frac{\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{1/2}^{1}\frac{\mathop{\sum }_{a\in \mathbb{Z}/p\mathbb{Z}}|1_{B(S,t\unicode[STIX]{x1D70C})}(a)-1_{B(S,t\unicode[STIX]{x1D70C})-h}(a)|}{|B(S,t\unicode[STIX]{x1D70C})|}\,dt\ll |S|\frac{\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
By the triangle inequality, the integrand here is bounded above by
![]() $2$
. Also, from (4.1), we see that any
$2$
. Also, from (4.1), we see that any
![]() $a$
for which
$a$
for which
 $1_{B(S,t\unicode[STIX]{x1D70C})-h}(a)\neq 1_{B(S,t\unicode[STIX]{x1D70C})}(a)$
lies in the “annulus”
$1_{B(S,t\unicode[STIX]{x1D70C})-h}(a)\neq 1_{B(S,t\unicode[STIX]{x1D70C})}(a)$
lies in the “annulus”
 $B(S,t\unicode[STIX]{x1D70C}+\unicode[STIX]{x1D70C}^{\prime })\backslash B(S,t\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}^{\prime })$
. We conclude that the left-hand side of (4.4) is bounded by
$B(S,t\unicode[STIX]{x1D70C}+\unicode[STIX]{x1D70C}^{\prime })\backslash B(S,t\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}^{\prime })$
. We conclude that the left-hand side of (4.4) is bounded by
 $$\begin{eqnarray}\int _{1/2}^{1}O\biggl(\min \biggl(\frac{|B(S,t\unicode[STIX]{x1D70C}+\unicode[STIX]{x1D70C}^{\prime })|-|B(S,t\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}^{\prime })|}{|B(S,t\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}^{\prime })|},1\biggr)\biggr)\,dt\end{eqnarray}$$
$$\begin{eqnarray}\int _{1/2}^{1}O\biggl(\min \biggl(\frac{|B(S,t\unicode[STIX]{x1D70C}+\unicode[STIX]{x1D70C}^{\prime })|-|B(S,t\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}^{\prime })|}{|B(S,t\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}^{\prime })|},1\biggr)\biggr)\,dt\end{eqnarray}$$
which, using the elementary bound
 $\min (x-1,1)\ll \log x$
for
$\min (x-1,1)\ll \log x$
for
![]() $x\geqslant 1$
, can be bounded in turn by
$x\geqslant 1$
, can be bounded in turn by
 $$\begin{eqnarray}O\biggl(\int _{1/2}^{1}\log \frac{|B(S,t\unicode[STIX]{x1D70C}+\unicode[STIX]{x1D70C}^{\prime })|}{|B(S,t\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}^{\prime })|}\,dt\biggr).\end{eqnarray}$$
$$\begin{eqnarray}O\biggl(\int _{1/2}^{1}\log \frac{|B(S,t\unicode[STIX]{x1D70C}+\unicode[STIX]{x1D70C}^{\prime })|}{|B(S,t\unicode[STIX]{x1D70C}-\unicode[STIX]{x1D70C}^{\prime })|}\,dt\biggr).\end{eqnarray}$$
The integral telescopes to
 $$\begin{eqnarray}O\biggl(\int _{1}^{1+\unicode[STIX]{x1D70C}^{\prime }/\unicode[STIX]{x1D70C}}\log |B(S,t\unicode[STIX]{x1D70C})|\,dt-\int _{1/2-\unicode[STIX]{x1D70C}^{\prime }/\unicode[STIX]{x1D70C}}^{1/2}\log |B(S,t\unicode[STIX]{x1D70C})|\,dt\biggr)\end{eqnarray}$$
$$\begin{eqnarray}O\biggl(\int _{1}^{1+\unicode[STIX]{x1D70C}^{\prime }/\unicode[STIX]{x1D70C}}\log |B(S,t\unicode[STIX]{x1D70C})|\,dt-\int _{1/2-\unicode[STIX]{x1D70C}^{\prime }/\unicode[STIX]{x1D70C}}^{1/2}\log |B(S,t\unicode[STIX]{x1D70C})|\,dt\biggr)\end{eqnarray}$$
which can be bounded in turn by
 $$\begin{eqnarray}O\biggl(\frac{\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x1D70C}}\log \frac{|B(S,2\unicode[STIX]{x1D70C})|}{|B(S,\unicode[STIX]{x1D70C}/4)|}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}O\biggl(\frac{\unicode[STIX]{x1D70C}^{\prime }}{\unicode[STIX]{x1D70C}}\log \frac{|B(S,2\unicode[STIX]{x1D70C})|}{|B(S,\unicode[STIX]{x1D70C}/4)|}\biggr).\end{eqnarray}$$
The claim now follows from Lemma 4.2. ◻
We will be interested in the Fourier coefficients
 $\mathbb{E}e_{p}(\unicode[STIX]{x1D706}\mathbf{n})=\mathbb{E}e(\unicode[STIX]{x1D706}\mathbf{n}/p)$
of random variables
$\mathbb{E}e_{p}(\unicode[STIX]{x1D706}\mathbf{n})=\mathbb{E}e(\unicode[STIX]{x1D706}\mathbf{n}/p)$
of random variables
![]() $\mathbf{n}$
drawn regularly from Bohr sets
$\mathbf{n}$
drawn regularly from Bohr sets
![]() $B(S,\unicode[STIX]{x1D70C})$
. As was noted by Bourgain [Reference Bourgain6], these coefficients are controlled by a “word norm”
$B(S,\unicode[STIX]{x1D70C})$
. As was noted by Bourgain [Reference Bourgain6], these coefficients are controlled by a “word norm”
![]() $\Vert \Vert _{S}$
, defined as follows.
$\Vert \Vert _{S}$
, defined as follows.
Definition 4.5 (Word norm).
If
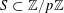 $S\subset \mathbb{Z}/p\mathbb{Z}$
is non-degenerate, and
$S\subset \mathbb{Z}/p\mathbb{Z}$
is non-degenerate, and
![]() $a$
is an element of
$a$
is an element of
![]() $\mathbb{Z}/p\mathbb{Z}$
, we define the word norm
$\mathbb{Z}/p\mathbb{Z}$
, we define the word norm
![]() $\Vert a\Vert _{S}$
of
$\Vert a\Vert _{S}$
of
![]() $a$
to be the minimum value of
$a$
to be the minimum value of
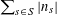 $\sum _{s\in S}|n_{s}|$
, where
$\sum _{s\in S}|n_{s}|$
, where
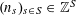 $(n_{s})_{s\in S}\in \mathbb{Z}^{S}$
ranges over tuples of integers such that one has a representation
$(n_{s})_{s\in S}\in \mathbb{Z}^{S}$
ranges over tuples of integers such that one has a representation
 $a=\sum _{s\in S}n_{s}s$
; note that such a representation always exists because
$a=\sum _{s\in S}n_{s}s$
; note that such a representation always exists because
![]() $S$
is non-degenerate.
$S$
is non-degenerate.
Similarly to (4.1), we observe the triangle inequalities
 $$\begin{eqnarray}\Vert a+b\Vert _{S}\leqslant \Vert a\Vert _{S}+\Vert b\Vert _{S};\qquad \Vert ka\Vert _{S}\leqslant |k|\Vert a\Vert _{S}\end{eqnarray}$$
$$\begin{eqnarray}\Vert a+b\Vert _{S}\leqslant \Vert a\Vert _{S}+\Vert b\Vert _{S};\qquad \Vert ka\Vert _{S}\leqslant |k|\Vert a\Vert _{S}\end{eqnarray}$$
for
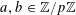 $a,b\in \mathbb{Z}/p\mathbb{Z}$
and
$a,b\in \mathbb{Z}/p\mathbb{Z}$
and
![]() $k\in \mathbb{Z}$
, which we will use frequently in the sequel, often without further comment.
$k\in \mathbb{Z}$
, which we will use frequently in the sequel, often without further comment.
We now give a duality relationship between the word norm
![]() $\Vert \Vert _{S}$
and the dual
$\Vert \Vert _{S}$
and the dual
![]() $S$
-norm
$S$
-norm
![]() $\Vert \Vert _{S^{\bot }}$
.
$\Vert \Vert _{S^{\bot }}$
.
Lemma 4.6 (Duality).
Let
![]() $S$
be a non-degenerate subset of
$S$
be a non-degenerate subset of
![]() $\mathbb{Z}/p\mathbb{Z}$
, and let
$\mathbb{Z}/p\mathbb{Z}$
, and let
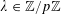 $\unicode[STIX]{x1D706}\in \mathbb{Z}/p\mathbb{Z}$
:
$\unicode[STIX]{x1D706}\in \mathbb{Z}/p\mathbb{Z}$
:
-
(i) for every
 $n\in \mathbb{Z}/p\mathbb{Z}$
, one has
$n\in \mathbb{Z}/p\mathbb{Z}$
, one has
 $\Vert n\unicode[STIX]{x1D706}/p\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant \Vert n\Vert _{S^{\bot }}\Vert \unicode[STIX]{x1D706}\Vert _{S}$
;
$\Vert n\unicode[STIX]{x1D706}/p\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant \Vert n\Vert _{S^{\bot }}\Vert \unicode[STIX]{x1D706}\Vert _{S}$
; -
(ii) conversely, if one has the estimate
 $\Vert n\unicode[STIX]{x1D706}/p\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant A\Vert n\Vert _{S^{\bot }}$
for some
$\Vert n\unicode[STIX]{x1D706}/p\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant A\Vert n\Vert _{S^{\bot }}$
for some
 $A\geqslant 1$
and all
$A\geqslant 1$
and all
 $n\in \mathbb{Z}/p\mathbb{Z}$
, then
$n\in \mathbb{Z}/p\mathbb{Z}$
, then
 $\Vert \unicode[STIX]{x1D706}\Vert _{S}\ll |S|^{3/2}A$
.
$\Vert \unicode[STIX]{x1D706}\Vert _{S}\ll |S|^{3/2}A$
.
Proof. To prove (i), we simply observe (using (2.4)) that for any
 $n\in \mathbb{Z}/p\mathbb{Z}$
, one has
$n\in \mathbb{Z}/p\mathbb{Z}$
, one has
 $$\begin{eqnarray}\displaystyle & & \displaystyle \Vert n\unicode[STIX]{x1D706}/p\Vert _{\mathbb{R}/\mathbb{Z}}\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl\|\mathop{\sum }_{\unicode[STIX]{x1D709}\in S}a_{\unicode[STIX]{x1D709}}\frac{n\unicode[STIX]{x1D709}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \mathop{\sum }_{\unicode[STIX]{x1D709}\in S}|a_{\unicode[STIX]{x1D709}}|\biggl\|\frac{n\unicode[STIX]{x1D709}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \mathop{\sum }_{\unicode[STIX]{x1D709}\in S}|a_{\unicode[STIX]{x1D709}}|\Vert n\Vert _{S^{\bot }}\leqslant \Vert \unicode[STIX]{x1D706}\Vert _{S}\Vert n\Vert _{S^{\bot }}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \Vert n\unicode[STIX]{x1D706}/p\Vert _{\mathbb{R}/\mathbb{Z}}\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl\|\mathop{\sum }_{\unicode[STIX]{x1D709}\in S}a_{\unicode[STIX]{x1D709}}\frac{n\unicode[STIX]{x1D709}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \mathop{\sum }_{\unicode[STIX]{x1D709}\in S}|a_{\unicode[STIX]{x1D709}}|\biggl\|\frac{n\unicode[STIX]{x1D709}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \mathop{\sum }_{\unicode[STIX]{x1D709}\in S}|a_{\unicode[STIX]{x1D709}}|\Vert n\Vert _{S^{\bot }}\leqslant \Vert \unicode[STIX]{x1D706}\Vert _{S}\Vert n\Vert _{S^{\bot }}\nonumber\end{eqnarray}$$
as desired, where
 $\unicode[STIX]{x1D706}=\sum _{\unicode[STIX]{x1D709}\in S}a_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D709}$
is a representation of
$\unicode[STIX]{x1D706}=\sum _{\unicode[STIX]{x1D709}\in S}a_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D709}$
is a representation of
![]() $\unicode[STIX]{x1D706}$
that minimizes
$\unicode[STIX]{x1D706}$
that minimizes
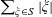 $\sum _{\unicode[STIX]{x1D709}\in S}|\unicode[STIX]{x1D709}|$
.
$\sum _{\unicode[STIX]{x1D709}\in S}|\unicode[STIX]{x1D709}|$
.
Estimates such as (ii) go back to the work of Bourgain [Reference Bourgain6]. We will prove this claim by a Fourier-analytic argument. We may assume that
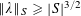 $\Vert \unicode[STIX]{x1D706}\Vert _{S}\geqslant |S|^{3/2}$
, as the claim is trivial otherwise. Let
$\Vert \unicode[STIX]{x1D706}\Vert _{S}\geqslant |S|^{3/2}$
, as the claim is trivial otherwise. Let
 $\unicode[STIX]{x1D713}:\mathbb{R}\rightarrow \mathbb{R}$
be a non-negative smooth even function (not depending on
$\unicode[STIX]{x1D713}:\mathbb{R}\rightarrow \mathbb{R}$
be a non-negative smooth even function (not depending on
![]() $p$
or
$p$
or
![]() $\unicode[STIX]{x1D706}$
) supported on
$\unicode[STIX]{x1D706}$
) supported on
![]() $[-1,1]$
and non-zero on
$[-1,1]$
and non-zero on
 $[-1/2,1/2]$
, whose Fourier transform
$[-1/2,1/2]$
, whose Fourier transform
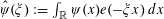 $\hat{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D709}):=\int _{\mathbb{R}}\unicode[STIX]{x1D713}(x)e(-\unicode[STIX]{x1D709}x)\,dx$
is also non-negative. Set
$\hat{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D709}):=\int _{\mathbb{R}}\unicode[STIX]{x1D713}(x)e(-\unicode[STIX]{x1D709}x)\,dx$
is also non-negative. Set
 $N:=|S|^{-1}\Vert \unicode[STIX]{x1D706}\Vert _{S}$
, so in particular
$N:=|S|^{-1}\Vert \unicode[STIX]{x1D706}\Vert _{S}$
, so in particular
![]() $N\geqslant 1$
. We consider the kernel
$N\geqslant 1$
. We consider the kernel
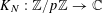 $K_{N}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
defined by
$K_{N}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
defined by
 $$\begin{eqnarray}K_{N}(n):=\mathop{\sum }_{k\in \mathbb{Z}}e_{p}(kn)\unicode[STIX]{x1D713}\biggl(\frac{k}{N}\biggr);\end{eqnarray}$$
$$\begin{eqnarray}K_{N}(n):=\mathop{\sum }_{k\in \mathbb{Z}}e_{p}(kn)\unicode[STIX]{x1D713}\biggl(\frac{k}{N}\biggr);\end{eqnarray}$$
by the Poisson summation formula we have
 $$\begin{eqnarray}K_{N}(n~(\operatorname{mod}~p))=N\mathop{\sum }_{m\in \mathbb{Z}}\hat{\unicode[STIX]{x1D713}}\biggl(\frac{Nn}{p}-Nm\biggr)\end{eqnarray}$$
$$\begin{eqnarray}K_{N}(n~(\operatorname{mod}~p))=N\mathop{\sum }_{m\in \mathbb{Z}}\hat{\unicode[STIX]{x1D713}}\biggl(\frac{Nn}{p}-Nm\biggr)\end{eqnarray}$$
for any integer
![]() $n$
, so in particular
$n$
, so in particular
![]() $K_{N}$
is non-negative.
$K_{N}$
is non-negative.
By definition of
![]() $N$
, the frequency
$N$
, the frequency
![]() $\unicode[STIX]{x1D706}$
has no representations of the form
$\unicode[STIX]{x1D706}$
has no representations of the form
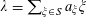 $\unicode[STIX]{x1D706}=\sum _{\unicode[STIX]{x1D709}\in S}a_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D709}$
with
$\unicode[STIX]{x1D706}=\sum _{\unicode[STIX]{x1D709}\in S}a_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D709}$
with
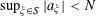 $\sup _{\unicode[STIX]{x1D709}\in S}|a_{\unicode[STIX]{x1D709}}|<N$
. Hence the Riesz-type product
$\sup _{\unicode[STIX]{x1D709}\in S}|a_{\unicode[STIX]{x1D709}}|<N$
. Hence the Riesz-type product
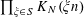 $\prod _{\unicode[STIX]{x1D709}\in S}K_{N}(\unicode[STIX]{x1D709}n)$
, when expanded, contains no terms of the form
$\prod _{\unicode[STIX]{x1D709}\in S}K_{N}(\unicode[STIX]{x1D709}n)$
, when expanded, contains no terms of the form
![]() $e_{p}(\unicode[STIX]{x1D706}n)$
or
$e_{p}(\unicode[STIX]{x1D706}n)$
or
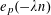 $e_{p}(-\unicode[STIX]{x1D706}n)$
, and is therefore orthogonal to
$e_{p}(-\unicode[STIX]{x1D706}n)$
, and is therefore orthogonal to
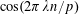 $\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D706}n/p)$
. In particular we have the identity
$\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D706}n/p)$
. In particular we have the identity
 $$\begin{eqnarray}\mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\mathop{\prod }_{\unicode[STIX]{x1D709}\in S}K_{N}(\unicode[STIX]{x1D709}n)=\mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\biggl(1-\cos \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D706}n}{p}\biggr)\biggr)\mathop{\prod }_{\unicode[STIX]{x1D709}\in S}K_{N}(\unicode[STIX]{x1D709}n).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\mathop{\prod }_{\unicode[STIX]{x1D709}\in S}K_{N}(\unicode[STIX]{x1D709}n)=\mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\biggl(1-\cos \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D706}n}{p}\biggr)\biggr)\mathop{\prod }_{\unicode[STIX]{x1D709}\in S}K_{N}(\unicode[STIX]{x1D709}n).\end{eqnarray}$$
On the other hand, from two applications of (2.3) we have
 $$\begin{eqnarray}\displaystyle 1-\cos \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D706}n}{p}\biggr) & \ll & \displaystyle \biggl\|\frac{\unicode[STIX]{x1D706}n}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}^{2}\leqslant A^{2}\Vert n\Vert _{S^{\bot }}^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle A^{2}\mathop{\sum }_{\unicode[STIX]{x1D709}_{0}\in S}\biggl\|\frac{\unicode[STIX]{x1D709}_{0}n}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}^{2}\leqslant A^{2}\mathop{\sum }_{\unicode[STIX]{x1D709}_{0}\in S}\biggl(1-\cos \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D709}_{0}n}{p}\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 1-\cos \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D706}n}{p}\biggr) & \ll & \displaystyle \biggl\|\frac{\unicode[STIX]{x1D706}n}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}^{2}\leqslant A^{2}\Vert n\Vert _{S^{\bot }}^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle A^{2}\mathop{\sum }_{\unicode[STIX]{x1D709}_{0}\in S}\biggl\|\frac{\unicode[STIX]{x1D709}_{0}n}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}^{2}\leqslant A^{2}\mathop{\sum }_{\unicode[STIX]{x1D709}_{0}\in S}\biggl(1-\cos \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D709}_{0}n}{p}\biggr)\biggr).\nonumber\end{eqnarray}$$
As
![]() $K_{N}$
is non-negative, we conclude that
$K_{N}$
is non-negative, we conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\mathop{\prod }_{\unicode[STIX]{x1D709}\in S}K_{N}(\unicode[STIX]{x1D709}n)\nonumber\\ \displaystyle & & \displaystyle \quad \ll A^{2}\mathop{\sum }_{\unicode[STIX]{x1D709}_{0}\in S}\mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\biggl(\biggl(\mathop{\prod }_{\unicode[STIX]{x1D709}\in S\backslash \unicode[STIX]{x1D709}_{0}}\!K_{\!N}(\unicode[STIX]{x1D709}n)\biggr)K_{\!N}(\unicode[STIX]{x1D709}_{0}n)\biggl(1-\cos \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D709}_{0}n}{p}\biggr)\biggr)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\mathop{\prod }_{\unicode[STIX]{x1D709}\in S}K_{N}(\unicode[STIX]{x1D709}n)\nonumber\\ \displaystyle & & \displaystyle \quad \ll A^{2}\mathop{\sum }_{\unicode[STIX]{x1D709}_{0}\in S}\mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\biggl(\biggl(\mathop{\prod }_{\unicode[STIX]{x1D709}\in S\backslash \unicode[STIX]{x1D709}_{0}}\!K_{\!N}(\unicode[STIX]{x1D709}n)\biggr)K_{\!N}(\unicode[STIX]{x1D709}_{0}n)\biggl(1-\cos \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D709}_{0}n}{p}\biggr)\biggr)\biggr).\end{eqnarray}$$
We can expand
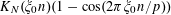 $K_{N}(\unicode[STIX]{x1D709}_{0}n)(1-\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D709}_{0}n/p))$
as a Fourier series
$K_{N}(\unicode[STIX]{x1D709}_{0}n)(1-\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D709}_{0}n/p))$
as a Fourier series
 $$\begin{eqnarray}\mathop{\sum }_{k\in \mathbb{Z}}e_{p}(kn)\biggl(\unicode[STIX]{x1D713}\biggl(\frac{k}{N}\biggr)-\frac{\unicode[STIX]{x1D713}((k-1)/N)+\unicode[STIX]{x1D713}((k+1)/N)}{2}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k\in \mathbb{Z}}e_{p}(kn)\biggl(\unicode[STIX]{x1D713}\biggl(\frac{k}{N}\biggr)-\frac{\unicode[STIX]{x1D713}((k-1)/N)+\unicode[STIX]{x1D713}((k+1)/N)}{2}\biggr).\end{eqnarray}$$
The expression inside parentheses is only non-vanishing for
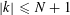 $|k|\leqslant N+1$
, and has magnitude
$|k|\leqslant N+1$
, and has magnitude
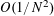 $O(1/N^{2})$
. As
$O(1/N^{2})$
. As
![]() $\unicode[STIX]{x1D713}$
is non-negative everywhere and non-zero on
$\unicode[STIX]{x1D713}$
is non-negative everywhere and non-zero on
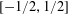 $[-1/2,1/2]$
, we thus have a pointwise estimate of the form
$[-1/2,1/2]$
, we thus have a pointwise estimate of the form
 $$\begin{eqnarray}\unicode[STIX]{x1D713}\biggl(\frac{k}{N}\biggr)-\frac{\unicode[STIX]{x1D713}((k-1)/N)+\unicode[STIX]{x1D713}((k+1)/N)}{2}\ll \frac{1}{N^{2}}\mathop{\sum }_{j=-8}^{8}\unicode[STIX]{x1D713}\biggl(\frac{k}{N}-\frac{j}{4}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}\biggl(\frac{k}{N}\biggr)-\frac{\unicode[STIX]{x1D713}((k-1)/N)+\unicode[STIX]{x1D713}((k+1)/N)}{2}\ll \frac{1}{N^{2}}\mathop{\sum }_{j=-8}^{8}\unicode[STIX]{x1D713}\biggl(\frac{k}{N}-\frac{j}{4}\biggr)\end{eqnarray}$$
(for example). By using the non-negativity of the Fourier coefficients of
![]() $K_{N}$
, this gives the estimate
$K_{N}$
, this gives the estimate
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\biggl(\mathop{\prod }_{\unicode[STIX]{x1D709}\in S\backslash \unicode[STIX]{x1D709}_{0}}K_{N}(\unicode[STIX]{x1D709}n)\biggr)K_{N}(\unicode[STIX]{x1D709}_{0}n)\biggl(1-\cos \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D709}_{0}n}{p}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \ll \frac{1}{N^{2}}\mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\mathop{\prod }_{\unicode[STIX]{x1D709}\in S}K_{N}(\unicode[STIX]{x1D709}n).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\biggl(\mathop{\prod }_{\unicode[STIX]{x1D709}\in S\backslash \unicode[STIX]{x1D709}_{0}}K_{N}(\unicode[STIX]{x1D709}n)\biggr)K_{N}(\unicode[STIX]{x1D709}_{0}n)\biggl(1-\cos \biggl(\frac{2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D709}_{0}n}{p}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \ll \frac{1}{N^{2}}\mathbb{E}_{n\in \mathbb{Z}/p\mathbb{Z}}\mathop{\prod }_{\unicode[STIX]{x1D709}\in S}K_{N}(\unicode[STIX]{x1D709}n).\nonumber\end{eqnarray}$$
Comparing this with (4.6), we conclude that
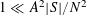 $1\ll A^{2}|S|/N^{2}$
, and the claim follows from the definition of
$1\ll A^{2}|S|/N^{2}$
, and the claim follows from the definition of
![]() $N$
.◻
$N$
.◻
Next, we estimate the Fourier coefficients of a regular distribution on a Bohr set in terms of the word norm.
Lemma 4.7. Let
![]() $S$
be a non-degenerate subset of
$S$
be a non-degenerate subset of
![]() $\mathbb{Z}/p\mathbb{Z}$
. Suppose that
$\mathbb{Z}/p\mathbb{Z}$
. Suppose that
![]() $\mathbf{n}$
is drawn regularly from
$\mathbf{n}$
is drawn regularly from
![]() $B(S,\unicode[STIX]{x1D70C})$
. Then we have
$B(S,\unicode[STIX]{x1D70C})$
. Then we have
 $$\begin{eqnarray}\mathbb{E}e_{p}(\unicode[STIX]{x1D706}\mathbf{n})\ll \frac{|S|^{5/2}}{\unicode[STIX]{x1D70C}\Vert \unicode[STIX]{x1D706}\Vert _{S}}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}e_{p}(\unicode[STIX]{x1D706}\mathbf{n})\ll \frac{|S|^{5/2}}{\unicode[STIX]{x1D70C}\Vert \unicode[STIX]{x1D706}\Vert _{S}}\end{eqnarray}$$
for all
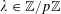 $\unicode[STIX]{x1D706}\in \mathbb{Z}/p\mathbb{Z}$
, where we adopt the convention that the above estimate is vacuously true if
$\unicode[STIX]{x1D706}\in \mathbb{Z}/p\mathbb{Z}$
, where we adopt the convention that the above estimate is vacuously true if
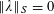 $\Vert \unicode[STIX]{x1D706}\Vert _{S}=0$
.
$\Vert \unicode[STIX]{x1D706}\Vert _{S}=0$
.
Proof. For any
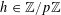 $h\in \mathbb{Z}/p\mathbb{Z}$
, one has from Lemma 4.4 that
$h\in \mathbb{Z}/p\mathbb{Z}$
, one has from Lemma 4.4 that
 $$\begin{eqnarray}\mathbb{E}e_{p}(\unicode[STIX]{x1D706}\mathbf{n})=\mathbb{E}e_{p}(\unicode[STIX]{x1D706}(\mathbf{n}+h))+O\biggl(\frac{|S|\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}e_{p}(\unicode[STIX]{x1D706}\mathbf{n})=\mathbb{E}e_{p}(\unicode[STIX]{x1D706}(\mathbf{n}+h))+O\biggl(\frac{|S|\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}}\biggr)\end{eqnarray}$$
which we may rearrange as
 $$\begin{eqnarray}(1-e_{p}(\unicode[STIX]{x1D706}h))\mathbb{E}e_{p}(\unicode[STIX]{x1D706}\mathbf{n})\ll \frac{|S|\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
$$\begin{eqnarray}(1-e_{p}(\unicode[STIX]{x1D706}h))\mathbb{E}e_{p}(\unicode[STIX]{x1D706}\mathbf{n})\ll \frac{|S|\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
Since
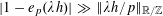 $|1-e_{p}(\unicode[STIX]{x1D706}h)|\gg \Vert \unicode[STIX]{x1D706}h/p\Vert _{\mathbb{R}/\mathbb{Z}}$
, we conclude that
$|1-e_{p}(\unicode[STIX]{x1D706}h)|\gg \Vert \unicode[STIX]{x1D706}h/p\Vert _{\mathbb{R}/\mathbb{Z}}$
, we conclude that
 $$\begin{eqnarray}\biggl\|\frac{\unicode[STIX]{x1D706}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\mathbb{E}e_{p}(\unicode[STIX]{x1D706}\mathbf{n})\ll \frac{|S|\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl\|\frac{\unicode[STIX]{x1D706}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\mathbb{E}e_{p}(\unicode[STIX]{x1D706}\mathbf{n})\ll \frac{|S|\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}}.\end{eqnarray}$$
Taking
![]() $h$
so as to minimize the ratio
$h$
so as to minimize the ratio
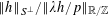 $\Vert h\Vert _{S^{\bot }}/\Vert \unicode[STIX]{x1D706}h/p\Vert _{\mathbb{R}/\mathbb{Z}}$
, the claim follows from Lemma 4.6.◻
$\Vert h\Vert _{S^{\bot }}/\Vert \unicode[STIX]{x1D706}h/p\Vert _{\mathbb{R}/\mathbb{Z}}$
, the claim follows from Lemma 4.6.◻
We will take advantage of the fact that Bohr sets can be approximately described as generalized arithmetic progressions. A key lemma in this regard is the following.
Lemma 4.8. Let
![]() $\unicode[STIX]{x1D6E4}$
be a lattice in
$\unicode[STIX]{x1D6E4}$
be a lattice in
![]() $\mathbb{R}^{d}$
. Then there exist linearly independent generators
$\mathbb{R}^{d}$
. Then there exist linearly independent generators
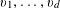 $v_{1},\ldots ,v_{d}$
of
$v_{1},\ldots ,v_{d}$
of
![]() $\unicode[STIX]{x1D6E4}$
and real numbers
$\unicode[STIX]{x1D6E4}$
and real numbers
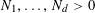 $N_{1},\ldots ,N_{d}>0$
such that
$N_{1},\ldots ,N_{d}>0$
such that
 $$\begin{eqnarray}B_{\mathbb{R}^{d}}(0,O(d)^{-3d/2}t)\cap \unicode[STIX]{x1D6E4}\subset \biggl\{\mathop{\sum }_{i=1}^{d}n_{i}v_{i}:|n_{i}|<tN_{i}\biggr\}\subset B_{\mathbb{R}^{d}}(0,t)\cap \unicode[STIX]{x1D6E4}\end{eqnarray}$$
$$\begin{eqnarray}B_{\mathbb{R}^{d}}(0,O(d)^{-3d/2}t)\cap \unicode[STIX]{x1D6E4}\subset \biggl\{\mathop{\sum }_{i=1}^{d}n_{i}v_{i}:|n_{i}|<tN_{i}\biggr\}\subset B_{\mathbb{R}^{d}}(0,t)\cap \unicode[STIX]{x1D6E4}\end{eqnarray}$$
for all
![]() $t>0$
, where
$t>0$
, where
 $B_{\mathbb{R}^{d}}(0,r)$
is the open Euclidean ball of radius
$B_{\mathbb{R}^{d}}(0,r)$
is the open Euclidean ball of radius
![]() $r$
in
$r$
in
![]() $\mathbb{R}^{d}$
, and the
$\mathbb{R}^{d}$
, and the
![]() $n_{i}$
are understood to be integers. Furthermore, the determinant/covolume
$n_{i}$
are understood to be integers. Furthermore, the determinant/covolume
![]() $\det (\unicode[STIX]{x1D6E4})$
obeys the bounds
$\det (\unicode[STIX]{x1D6E4})$
obeys the bounds
 $$\begin{eqnarray}\det (\unicode[STIX]{x1D6E4})=(2d)^{O(d)}\mathop{\prod }_{i=1}^{d}N_{i}^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\det (\unicode[STIX]{x1D6E4})=(2d)^{O(d)}\mathop{\prod }_{i=1}^{d}N_{i}^{-1}.\end{eqnarray}$$
Proof. Applying [Reference Tao and Vu34, Theorem 1.6], we can find elements
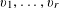 $v_{1},\ldots ,v_{r}$
of
$v_{1},\ldots ,v_{r}$
of
![]() $\unicode[STIX]{x1D6E4}$
for some
$\unicode[STIX]{x1D6E4}$
for some
![]() $r\leqslant d$
, linearly independent over the rationals, and real numbers
$r\leqslant d$
, linearly independent over the rationals, and real numbers
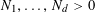 $N_{1},\ldots ,N_{d}>0$
such that
$N_{1},\ldots ,N_{d}>0$
such that
 $$\begin{eqnarray}B_{\mathbb{R}^{d}}(0,O(d)^{-3d/2}t)\cap \unicode[STIX]{x1D6E4}\subset \biggl\{\mathop{\sum }_{i=1}^{r}n_{i}v_{i}:|n_{i}|<tN_{i}\biggr\}\subset B_{\mathbb{R}^{d}}(0,t)\cap \unicode[STIX]{x1D6E4}\end{eqnarray}$$
$$\begin{eqnarray}B_{\mathbb{R}^{d}}(0,O(d)^{-3d/2}t)\cap \unicode[STIX]{x1D6E4}\subset \biggl\{\mathop{\sum }_{i=1}^{r}n_{i}v_{i}:|n_{i}|<tN_{i}\biggr\}\subset B_{\mathbb{R}^{d}}(0,t)\cap \unicode[STIX]{x1D6E4}\end{eqnarray}$$
for all
![]() $t>0$
, and such that
$t>0$
, and such that
 $$\begin{eqnarray}O(d)^{-7d/2}|B_{\mathbb{ R}^{d}}(0,t)\cap \unicode[STIX]{x1D6E4}|\leqslant \biggl|\biggl\{\mathop{\sum }_{i=1}^{r}n_{i}v_{i}:|n_{i}|<tN_{i}\biggr\}\biggr|\leqslant |B_{\mathbb{R}^{d}}(0,t)\cap \unicode[STIX]{x1D6E4}|.\end{eqnarray}$$
$$\begin{eqnarray}O(d)^{-7d/2}|B_{\mathbb{ R}^{d}}(0,t)\cap \unicode[STIX]{x1D6E4}|\leqslant \biggl|\biggl\{\mathop{\sum }_{i=1}^{r}n_{i}v_{i}:|n_{i}|<tN_{i}\biggr\}\biggr|\leqslant |B_{\mathbb{R}^{d}}(0,t)\cap \unicode[STIX]{x1D6E4}|.\end{eqnarray}$$
(Strictly speaking, the statement of [Reference Tao and Vu34, Theorem 1.6] only claims the latter bound for
![]() $t=1$
, but the same argument gives the bound for all
$t=1$
, but the same argument gives the bound for all
![]() $t>0$
.) Sending
$t>0$
.) Sending
![]() $t$
to infinity, we conclude that the
$t$
to infinity, we conclude that the
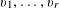 $v_{1},\ldots ,v_{r}$
generate
$v_{1},\ldots ,v_{r}$
generate
![]() $\unicode[STIX]{x1D6E4}$
; since, by virtue of being a lattice,
$\unicode[STIX]{x1D6E4}$
; since, by virtue of being a lattice,
![]() $\unicode[STIX]{x1D6E4}$
is cocompact, this forces
$\unicode[STIX]{x1D6E4}$
is cocompact, this forces
![]() $d=r$
. Also, volume packing arguments show that as
$d=r$
. Also, volume packing arguments show that as
![]() $t\rightarrow \infty$
, the cardinality
$t\rightarrow \infty$
, the cardinality
 $|B_{\mathbb{R}^{d}}(0,t)\,\cap \,\unicode[STIX]{x1D6E4}|$
is asymptotic to the measure of
$|B_{\mathbb{R}^{d}}(0,t)\,\cap \,\unicode[STIX]{x1D6E4}|$
is asymptotic to the measure of
 $B_{\mathbb{R}^{d}}(0,t)$
divided by
$B_{\mathbb{R}^{d}}(0,t)$
divided by
![]() $\det (\unicode[STIX]{x1D6E4})$
, while the cardinality of
$\det (\unicode[STIX]{x1D6E4})$
, while the cardinality of
 $|\{n_{1}v_{1}+\cdots +n_{d}v_{d}:|n_{i}|\leqslant tN_{i}\}|$
is asymptotic to
$|\{n_{1}v_{1}+\cdots +n_{d}v_{d}:|n_{i}|\leqslant tN_{i}\}|$
is asymptotic to
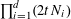 $\prod _{i=1}^{d}(2tN_{i})$
. We conclude (4.8) as desired.◻
$\prod _{i=1}^{d}(2tN_{i})$
. We conclude (4.8) as desired.◻
The following corollary describes how we may pick a “basis” for a Bohr set.
Corollary 4.9. Let
![]() $S$
be a non-degenerate subset of
$S$
be a non-degenerate subset of
![]() $\mathbb{Z}/p\mathbb{Z}$
, and set
$\mathbb{Z}/p\mathbb{Z}$
, and set
![]() $d:=|S|$
. Then there exist elements
$d:=|S|$
. Then there exist elements
 $a_{1},\ldots ,a_{d}$
of
$a_{1},\ldots ,a_{d}$
of
![]() $\mathbb{Z}/p\mathbb{Z}$
and real numbers
$\mathbb{Z}/p\mathbb{Z}$
and real numbers
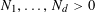 $N_{1},\ldots ,N_{d}>0$
such that
$N_{1},\ldots ,N_{d}>0$
such that
 $$\begin{eqnarray}\mathop{\prod }_{i=1}^{d}N_{i}^{-1}=(2d)^{O(d)}p\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{i=1}^{d}N_{i}^{-1}=(2d)^{O(d)}p\end{eqnarray}$$
and
 $$\begin{eqnarray}\Vert a_{i}\Vert _{S^{\bot }}\leqslant N_{i}^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\Vert a_{i}\Vert _{S^{\bot }}\leqslant N_{i}^{-1}\end{eqnarray}$$
for all
 $i=1,\ldots ,d$
. Furthermore, for any
$i=1,\ldots ,d$
. Furthermore, for any
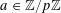 $a\in \mathbb{Z}/p\mathbb{Z}$
, there exists a representation
$a\in \mathbb{Z}/p\mathbb{Z}$
, there exists a representation
 $$\begin{eqnarray}a=n_{1}a_{1}+\cdots +n_{d}a_{d}\end{eqnarray}$$
$$\begin{eqnarray}a=n_{1}a_{1}+\cdots +n_{d}a_{d}\end{eqnarray}$$
with
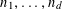 $n_{1},\ldots ,n_{d}$
integers of size
$n_{1},\ldots ,n_{d}$
integers of size
 $$\begin{eqnarray}n_{i}=(2d)^{O(d)}N_{i}\Vert a\Vert _{S^{\bot }}\end{eqnarray}$$
$$\begin{eqnarray}n_{i}=(2d)^{O(d)}N_{i}\Vert a\Vert _{S^{\bot }}\end{eqnarray}$$
for
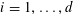 $i=1,\ldots ,d$
. Finally, if one imposes the additional condition
$i=1,\ldots ,d$
. Finally, if one imposes the additional condition
 $|n_{i}|<N_{i}/2$
for all
$|n_{i}|<N_{i}/2$
for all
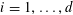 $i=1,\ldots ,d$
, then there is at most one such representation of this form (4.12) for a given
$i=1,\ldots ,d$
, then there is at most one such representation of this form (4.12) for a given
![]() $a$
.
$a$
.
Proof. For each
![]() $s\in S$
, the fraction
$s\in S$
, the fraction
![]() $s/p$
can be viewed as an element of
$s/p$
can be viewed as an element of
![]() $\mathbb{R}/\mathbb{Z}$
of order at most
$\mathbb{R}/\mathbb{Z}$
of order at most
![]() $p$
; as
$p$
; as
![]() $S$
is non-degenerate, we see that the tuple
$S$
is non-degenerate, we see that the tuple
 $(s/p)_{s\in S}$
is an element of the torus
$(s/p)_{s\in S}$
is an element of the torus
![]() $(\mathbb{R}/\mathbb{Z})^{S}$
of order
$(\mathbb{R}/\mathbb{Z})^{S}$
of order
![]() $p$
. Let
$p$
. Let
![]() $\unicode[STIX]{x1D6E4}$
be the preimage in
$\unicode[STIX]{x1D6E4}$
be the preimage in
![]() $\mathbb{R}^{S}$
of the group generated by this element, thus
$\mathbb{R}^{S}$
of the group generated by this element, thus
![]() $\unicode[STIX]{x1D6E4}$
is a lattice of
$\unicode[STIX]{x1D6E4}$
is a lattice of
![]() $\mathbb{R}^{S}$
that contains
$\mathbb{R}^{S}$
that contains
![]() $\mathbb{Z}^{S}$
as a sublattice of index
$\mathbb{Z}^{S}$
as a sublattice of index
![]() $p$
; in particular,
$p$
; in particular,
![]() $\unicode[STIX]{x1D6E4}$
has determinant
$\unicode[STIX]{x1D6E4}$
has determinant
![]() $p$
. Applying Lemma 4.8, one can find generators
$p$
. Applying Lemma 4.8, one can find generators
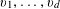 $v_{1},\ldots ,v_{d}$
of
$v_{1},\ldots ,v_{d}$
of
![]() $\unicode[STIX]{x1D6E4}$
and real numbers
$\unicode[STIX]{x1D6E4}$
and real numbers
 $N_{1},\ldots ,N_{d}$
obeying (4.10) such that
$N_{1},\ldots ,N_{d}$
obeying (4.10) such that
 $$\begin{eqnarray}B_{\mathbb{R}^{S}}(0,O(d)^{-3d/2}t)\cap \unicode[STIX]{x1D6E4}\subset \biggl\{\mathop{\sum }_{i=1}^{d}n_{i}v_{i}:|n_{i}|<tN_{i}\biggr\}\subset B_{\mathbb{R}^{S}}(0,t)\cap \unicode[STIX]{x1D6E4}\end{eqnarray}$$
$$\begin{eqnarray}B_{\mathbb{R}^{S}}(0,O(d)^{-3d/2}t)\cap \unicode[STIX]{x1D6E4}\subset \biggl\{\mathop{\sum }_{i=1}^{d}n_{i}v_{i}:|n_{i}|<tN_{i}\biggr\}\subset B_{\mathbb{R}^{S}}(0,t)\cap \unicode[STIX]{x1D6E4}\end{eqnarray}$$
for all
![]() $t>0$
.
$t>0$
.
By construction of
![]() $\unicode[STIX]{x1D6E4}$
, we can find elements
$\unicode[STIX]{x1D6E4}$
, we can find elements
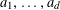 $a_{1},\ldots ,a_{d}$
of
$a_{1},\ldots ,a_{d}$
of
![]() $\mathbb{Z}/p\mathbb{Z}$
such that
$\mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}v_{i}=\biggl(\frac{a_{i}s}{p}\biggr)_{s\in S}\quad (\operatorname{mod}~\mathbb{Z}^{S})\end{eqnarray}$$
$$\begin{eqnarray}v_{i}=\biggl(\frac{a_{i}s}{p}\biggr)_{s\in S}\quad (\operatorname{mod}~\mathbb{Z}^{S})\end{eqnarray}$$
for
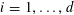 $i=1,\ldots ,d$
. Applying (4.14) with
$i=1,\ldots ,d$
. Applying (4.14) with
![]() $t$
slightly larger than
$t$
slightly larger than
![]() $N_{i}^{-1}$
for some
$N_{i}^{-1}$
for some
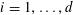 $i=1,\ldots ,d$
, we see that
$i=1,\ldots ,d$
, we see that
 $v_{i}\in B_{\mathbb{R}^{d}}(N_{i}^{-1})$
, and hence by (4.15) we have (4.11).
$v_{i}\in B_{\mathbb{R}^{d}}(N_{i}^{-1})$
, and hence by (4.15) we have (4.11).
Finally, if
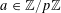 $a\in \mathbb{Z}/p\mathbb{Z}$
, then by definition of
$a\in \mathbb{Z}/p\mathbb{Z}$
, then by definition of
![]() $\unicode[STIX]{x1D6E4}$
we can find an element
$\unicode[STIX]{x1D6E4}$
we can find an element
![]() $x$
of
$x$
of
![]() $\unicode[STIX]{x1D6E4}$
in the preimage of
$\unicode[STIX]{x1D6E4}$
in the preimage of
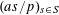 $(as/p)_{s\in S}$
such that each component of
$(as/p)_{s\in S}$
such that each component of
![]() $x$
has magnitude less than
$x$
has magnitude less than
![]() $\Vert a\Vert _{S^{\bot }}$
; in particular,
$\Vert a\Vert _{S^{\bot }}$
; in particular,
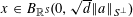 $x\in B_{\mathbb{R}^{S}}(0,\sqrt{d}\Vert a\Vert _{S^{\bot }})$
. Applying (4.14), we conclude that
$x\in B_{\mathbb{R}^{S}}(0,\sqrt{d}\Vert a\Vert _{S^{\bot }})$
. Applying (4.14), we conclude that
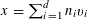 $x=\sum _{i=1}^{d}n_{i}v_{i}$
for some integers
$x=\sum _{i=1}^{d}n_{i}v_{i}$
for some integers
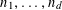 $n_{1},\ldots ,n_{d}$
obeying (4.13), giving the desired representation (4.12).
$n_{1},\ldots ,n_{d}$
obeying (4.13), giving the desired representation (4.12).
Finally, we show uniqueness. If there were two representations of the form (4.12) with
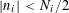 $|n_{i}|<N_{i}/2$
for all
$|n_{i}|<N_{i}/2$
for all
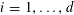 $i=1,\ldots ,d$
, then there exists a tuple
$i=1,\ldots ,d$
, then there exists a tuple
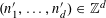 $(n_{1}^{\prime },\ldots ,n_{d}^{\prime })\in \mathbb{Z}^{d}$
, not identically zero, with
$(n_{1}^{\prime },\ldots ,n_{d}^{\prime })\in \mathbb{Z}^{d}$
, not identically zero, with
 $|n_{i}^{\prime }|<N_{i}$
for all
$|n_{i}^{\prime }|<N_{i}$
for all
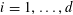 $i=1,\ldots ,d$
and
$i=1,\ldots ,d$
and
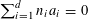 $\sum _{i=1}^{d}n_{i}a_{i}=0$
, which implies that the vector
$\sum _{i=1}^{d}n_{i}a_{i}=0$
, which implies that the vector
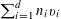 $\sum _{i=1}^{d}n_{i}v_{i}$
lies in
$\sum _{i=1}^{d}n_{i}v_{i}$
lies in
![]() $\mathbb{Z}^{S}$
. As the
$\mathbb{Z}^{S}$
. As the
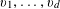 $v_{1},\ldots ,v_{d}$
are linearly independent, this vector must have magnitude at least
$v_{1},\ldots ,v_{d}$
are linearly independent, this vector must have magnitude at least
![]() $1$
; but this contradicts (4.7) (with
$1$
; but this contradicts (4.7) (with
![]() $t=1$
).◻
$t=1$
).◻
Linear and quadratic functions on Bohr sets
We will frequently need to deal with locally linear or quadratic functions on Bohr sets. We review the definitions of these now.
Definition 4.10. Let
![]() $B$
be a subset of
$B$
be a subset of
![]() $\mathbb{Z}/p\mathbb{Z}$
, and let
$\mathbb{Z}/p\mathbb{Z}$
, and let
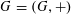 $G=(G,+)$
be an abelian group. A function
$G=(G,+)$
be an abelian group. A function
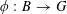 $\unicode[STIX]{x1D719}:B\rightarrow G$
is said to be locally linear on
$\unicode[STIX]{x1D719}:B\rightarrow G$
is said to be locally linear on
![]() $B$
if one has
$B$
if one has
 $$\begin{eqnarray}\unicode[STIX]{x1D719}(n+h_{1}+h_{2})-\unicode[STIX]{x1D719}(n+h_{1})-\unicode[STIX]{x1D719}(n+h_{2})+\unicode[STIX]{x1D719}(n)=0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}(n+h_{1}+h_{2})-\unicode[STIX]{x1D719}(n+h_{1})-\unicode[STIX]{x1D719}(n+h_{2})+\unicode[STIX]{x1D719}(n)=0\end{eqnarray}$$
whenever
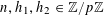 $n,h_{1},h_{2}\in \mathbb{Z}/p\mathbb{Z}$
are such that
$n,h_{1},h_{2}\in \mathbb{Z}/p\mathbb{Z}$
are such that
 $n,n+h_{1},n+h_{2},n+h_{1}+h_{2}\in B$
. Similarly,
$n,n+h_{1},n+h_{2},n+h_{1}+h_{2}\in B$
. Similarly,
![]() $\unicode[STIX]{x1D719}$
is said to be locally quadratic on
$\unicode[STIX]{x1D719}$
is said to be locally quadratic on
![]() $B$
if one has
$B$
if one has
 $$\begin{eqnarray}\mathop{\sum }_{(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}}(-1)^{\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D714}_{2}+\unicode[STIX]{x1D714}_{3}}\unicode[STIX]{x1D719}(n+\unicode[STIX]{x1D714}_{1}h_{1}+\unicode[STIX]{x1D714}_{2}h_{2}+\unicode[STIX]{x1D714}_{3}h_{3})=0\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}}(-1)^{\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D714}_{2}+\unicode[STIX]{x1D714}_{3}}\unicode[STIX]{x1D719}(n+\unicode[STIX]{x1D714}_{1}h_{1}+\unicode[STIX]{x1D714}_{2}h_{2}+\unicode[STIX]{x1D714}_{3}h_{3})=0\end{eqnarray}$$
whenever
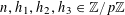 $n,h_{1},h_{2},h_{3}\in \mathbb{Z}/p\mathbb{Z}$
are such that
$n,h_{1},h_{2},h_{3}\in \mathbb{Z}/p\mathbb{Z}$
are such that
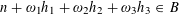 $n+\unicode[STIX]{x1D714}_{1}h_{1}+\unicode[STIX]{x1D714}_{2}h_{2}+\unicode[STIX]{x1D714}_{3}h_{3}\in B$
for all
$n+\unicode[STIX]{x1D714}_{1}h_{1}+\unicode[STIX]{x1D714}_{2}h_{2}+\unicode[STIX]{x1D714}_{3}h_{3}\in B$
for all
 $(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}$
.
$(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3})\in \{0,1\}^{3}$
.
A function
 $\unicode[STIX]{x1D713}:B\times B\rightarrow G$
is said to be locally bilinear on
$\unicode[STIX]{x1D713}:B\times B\rightarrow G$
is said to be locally bilinear on
![]() $B$
if one has
$B$
if one has
 $$\begin{eqnarray}\unicode[STIX]{x1D713}(h_{1}+h_{1}^{\prime },h_{2})=\unicode[STIX]{x1D713}(h_{1},h_{2})+\unicode[STIX]{x1D713}(h_{1}^{\prime },h_{2})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}(h_{1}+h_{1}^{\prime },h_{2})=\unicode[STIX]{x1D713}(h_{1},h_{2})+\unicode[STIX]{x1D713}(h_{1}^{\prime },h_{2})\end{eqnarray}$$
whenever
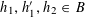 $h_{1},h_{1}^{\prime },h_{2}\in B$
are such that
$h_{1},h_{1}^{\prime },h_{2}\in B$
are such that
 $h_{1}+h_{1}^{\prime }\in B$
, and similarly one has
$h_{1}+h_{1}^{\prime }\in B$
, and similarly one has
 $$\begin{eqnarray}\unicode[STIX]{x1D713}(h_{1},h_{2}+h_{2}^{\prime })=\unicode[STIX]{x1D713}(h_{1},h_{2})+\unicode[STIX]{x1D713}(h_{1},h_{2}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}(h_{1},h_{2}+h_{2}^{\prime })=\unicode[STIX]{x1D713}(h_{1},h_{2})+\unicode[STIX]{x1D713}(h_{1},h_{2}^{\prime })\end{eqnarray}$$
whenever
 $h_{1},h_{2},h_{2}^{\prime }\in B$
are such that
$h_{1},h_{2},h_{2}^{\prime }\in B$
are such that
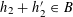 $h_{2}+h_{2}^{\prime }\in B$
.
$h_{2}+h_{2}^{\prime }\in B$
.
Specializing (4.16) to the case
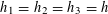 $h_{1}=h_{2}=h_{3}=h$
, we conclude that
$h_{1}=h_{2}=h_{3}=h$
, we conclude that
 $$\begin{eqnarray}\unicode[STIX]{x1D719}(n)-3\unicode[STIX]{x1D719}(n+h)+3\unicode[STIX]{x1D719}(n+2h)-\unicode[STIX]{x1D719}(n+3h)=0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}(n)-3\unicode[STIX]{x1D719}(n+h)+3\unicode[STIX]{x1D719}(n+2h)-\unicode[STIX]{x1D719}(n+3h)=0\end{eqnarray}$$
whenever
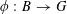 $\unicode[STIX]{x1D719}:B\rightarrow G$
is locally quadratic on
$\unicode[STIX]{x1D719}:B\rightarrow G$
is locally quadratic on
![]() $B$
and
$B$
and
 $n,n+h,n+2h,n+3h\in B$
.
$n,n+h,n+2h,n+3h\in B$
.
It is well known (from the Weyl exponential sum estimates) that quadratic exponential sums such as
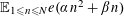 $\mathbb{E}_{1\leqslant n\leqslant N}e(\unicode[STIX]{x1D6FC}n^{2}+\unicode[STIX]{x1D6FD}n)$
can only be large when the quadratic phase
$\mathbb{E}_{1\leqslant n\leqslant N}e(\unicode[STIX]{x1D6FC}n^{2}+\unicode[STIX]{x1D6FD}n)$
can only be large when the quadratic phase
![]() $\unicode[STIX]{x1D6FC}n^{2}$
is of “major arc” type in the sense that
$\unicode[STIX]{x1D6FC}n^{2}$
is of “major arc” type in the sense that
![]() $k\unicode[STIX]{x1D6FC}n^{2}$
is close to constant on the range
$k\unicode[STIX]{x1D6FC}n^{2}$
is close to constant on the range
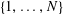 $\{1,\ldots ,N\}$
of the summation variable
$\{1,\ldots ,N\}$
of the summation variable
![]() $n$
, for some bounded positive integer
$n$
, for some bounded positive integer
![]() $k$
. The following proposition is an analogue of this phenomenon on Bohr sets.
$k$
. The following proposition is an analogue of this phenomenon on Bohr sets.
Proposition 4.11 (Large local quadratic exponential sums).
Let
![]() $B(S,\unicode[STIX]{x1D70C})$
be a Bohr set, let
$B(S,\unicode[STIX]{x1D70C})$
be a Bohr set, let
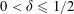 $0<\unicode[STIX]{x1D6FF}\leqslant 1/2$
, let
$0<\unicode[STIX]{x1D6FF}\leqslant 1/2$
, let
 $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}:B(S,10\unicode[STIX]{x1D70C})\rightarrow \mathbb{R}/\mathbb{Z}$
be locally linear maps, and let
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}:B(S,10\unicode[STIX]{x1D70C})\rightarrow \mathbb{R}/\mathbb{Z}$
be locally linear maps, and let
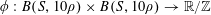 $\unicode[STIX]{x1D719}:B(S,10\unicode[STIX]{x1D70C})\times B(S,10\unicode[STIX]{x1D70C})\rightarrow \mathbb{R}/\mathbb{Z}$
be a locally bilinear phase such that
$\unicode[STIX]{x1D719}:B(S,10\unicode[STIX]{x1D70C})\times B(S,10\unicode[STIX]{x1D70C})\rightarrow \mathbb{R}/\mathbb{Z}$
be a locally bilinear phase such that
 $$\begin{eqnarray}|\mathbb{E}e(\unicode[STIX]{x1D719}(\mathbf{n},\mathbf{m})+\unicode[STIX]{x1D706}(\mathbf{n})+\unicode[STIX]{x1D707}(\mathbf{m}))|\geqslant \unicode[STIX]{x1D6FF}\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}e(\unicode[STIX]{x1D719}(\mathbf{n},\mathbf{m})+\unicode[STIX]{x1D706}(\mathbf{n})+\unicode[STIX]{x1D707}(\mathbf{m}))|\geqslant \unicode[STIX]{x1D6FF}\end{eqnarray}$$
if
![]() $\mathbf{n},\mathbf{m}$
are drawn independently and regularly from
$\mathbf{n},\mathbf{m}$
are drawn independently and regularly from
![]() $B(S,\unicode[STIX]{x1D70C})$
. Then there exists a natural number
$B(S,\unicode[STIX]{x1D70C})$
. Then there exists a natural number
 $$\begin{eqnarray}1\leqslant k\leqslant \unicode[STIX]{x1D6FF}^{-O(C_{1}|S|^{2})}\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant k\leqslant \unicode[STIX]{x1D6FF}^{-O(C_{1}|S|^{2})}\end{eqnarray}$$
such that
 $$\begin{eqnarray}\Vert k\unicode[STIX]{x1D719}(n,m)\Vert _{\mathbb{R}/\mathbb{Z}}\ll \unicode[STIX]{x1D6FF}^{-O(C_{1}|S|^{2})}\frac{\Vert n\Vert _{S}\Vert m\Vert _{S}}{\unicode[STIX]{x1D70C}^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert k\unicode[STIX]{x1D719}(n,m)\Vert _{\mathbb{R}/\mathbb{Z}}\ll \unicode[STIX]{x1D6FF}^{-O(C_{1}|S|^{2})}\frac{\Vert n\Vert _{S}\Vert m\Vert _{S}}{\unicode[STIX]{x1D70C}^{2}}\end{eqnarray}$$
whenever
 $n,m\in B(S,\unicode[STIX]{x1D6FF}^{C_{1}}\unicode[STIX]{x1D70C}/(C_{1}|S|)^{3|S|})$
.
$n,m\in B(S,\unicode[STIX]{x1D6FF}^{C_{1}}\unicode[STIX]{x1D70C}/(C_{1}|S|)^{3|S|})$
.
Proof. Let
![]() $d:=|S|$
, thus
$d:=|S|$
, thus
![]() $d\geqslant 1$
. By Corollary 4.9, we can find elements
$d\geqslant 1$
. By Corollary 4.9, we can find elements
 $a_{1},\ldots ,a_{d}$
of
$a_{1},\ldots ,a_{d}$
of
![]() $\mathbb{Z}/p\mathbb{Z}$
and real numbers
$\mathbb{Z}/p\mathbb{Z}$
and real numbers
 $N_{1},\ldots ,N_{d}$
obeying the conclusions of that corollary.
$N_{1},\ldots ,N_{d}$
obeying the conclusions of that corollary.
Suppose that
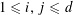 $1\leqslant i,j\leqslant d$
are such that
$1\leqslant i,j\leqslant d$
are such that
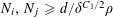 $N_{i},N_{j}\geqslant d/\unicode[STIX]{x1D6FF}^{C_{1}/2}\unicode[STIX]{x1D70C}$
(we allow
$N_{i},N_{j}\geqslant d/\unicode[STIX]{x1D6FF}^{C_{1}/2}\unicode[STIX]{x1D70C}$
(we allow
![]() $i$
and
$i$
and
![]() $j$
to be equal). Then by (4.11) we have
$j$
to be equal). Then by (4.11) we have
 $$\begin{eqnarray}\Vert a_{i}\Vert _{S^{\bot }},\Vert a_{j}\Vert _{S^{\bot }}\leqslant d^{-1}\unicode[STIX]{x1D6FF}^{C_{1}/2}\unicode[STIX]{x1D70C}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert a_{i}\Vert _{S^{\bot }},\Vert a_{j}\Vert _{S^{\bot }}\leqslant d^{-1}\unicode[STIX]{x1D6FF}^{C_{1}/2}\unicode[STIX]{x1D70C}.\end{eqnarray}$$
We can control the coefficient
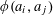 $\unicode[STIX]{x1D719}(a_{i},a_{j})$
by the following argument. If we draw
$\unicode[STIX]{x1D719}(a_{i},a_{j})$
by the following argument. If we draw
![]() $\mathbf{b}_{i}$
and
$\mathbf{b}_{i}$
and
![]() $\mathbf{b}_{j}$
uniformly from
$\mathbf{b}_{j}$
uniformly from
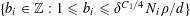 $\{b_{i}\in \mathbb{Z}:1\leqslant b_{i}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{i}\unicode[STIX]{x1D70C}/d\}$
and
$\{b_{i}\in \mathbb{Z}:1\leqslant b_{i}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{i}\unicode[STIX]{x1D70C}/d\}$
and
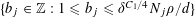 $\{b_{j}\in \mathbb{Z}:1\leqslant b_{j}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{j}\unicode[STIX]{x1D70C}/d\}$
respectively and independently of each other and of
$\{b_{j}\in \mathbb{Z}:1\leqslant b_{j}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{j}\unicode[STIX]{x1D70C}/d\}$
respectively and independently of each other and of
![]() $\mathbf{n},\mathbf{m}$
, then from two applications of Lemma 4.4 (comparing
$\mathbf{n},\mathbf{m}$
, then from two applications of Lemma 4.4 (comparing
![]() $\mathbf{n}$
with
$\mathbf{n}$
with
![]() $\mathbf{n}+\mathbf{b}_{i}a_{i}$
, and
$\mathbf{n}+\mathbf{b}_{i}a_{i}$
, and
![]() $\mathbf{m}$
with
$\mathbf{m}$
with
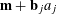 $\mathbf{m}+\mathbf{b}_{j}a_{j}$
) we have
$\mathbf{m}+\mathbf{b}_{j}a_{j}$
) we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}e(\unicode[STIX]{x1D719}(\mathbf{n}+\mathbf{b}_{i}a_{i},\mathbf{m}+\mathbf{b}_{j}a_{j})+\unicode[STIX]{x1D706}(\mathbf{n}+\mathbf{b}_{i}a_{i})+\unicode[STIX]{x1D707}(\mathbf{m}+\mathbf{b}_{j}a_{j}))\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbb{E}e(\unicode[STIX]{x1D719}(\mathbf{n},\mathbf{m})+\unicode[STIX]{x1D706}(\mathbf{n})+\unicode[STIX]{x1D707}(\mathbf{m}))+O(\unicode[STIX]{x1D6FF}^{C_{1}/4})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}e(\unicode[STIX]{x1D719}(\mathbf{n}+\mathbf{b}_{i}a_{i},\mathbf{m}+\mathbf{b}_{j}a_{j})+\unicode[STIX]{x1D706}(\mathbf{n}+\mathbf{b}_{i}a_{i})+\unicode[STIX]{x1D707}(\mathbf{m}+\mathbf{b}_{j}a_{j}))\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbb{E}e(\unicode[STIX]{x1D719}(\mathbf{n},\mathbf{m})+\unicode[STIX]{x1D706}(\mathbf{n})+\unicode[STIX]{x1D707}(\mathbf{m}))+O(\unicode[STIX]{x1D6FF}^{C_{1}/4})\nonumber\end{eqnarray}$$
and hence from (4.18) (assuming
![]() $C_{1}$
large enough) we have
$C_{1}$
large enough) we have
 $$\begin{eqnarray}|\mathbb{E}e(\unicode[STIX]{x1D719}(\mathbf{n}+\mathbf{b}_{i}a_{i},\mathbf{m}+\mathbf{b}_{j}a_{j})+\unicode[STIX]{x1D706}(\mathbf{n}+\mathbf{b}_{i}a_{i})+\unicode[STIX]{x1D707}(\mathbf{m}+\mathbf{b}_{j}a_{j}))|\gg \unicode[STIX]{x1D6FF}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}e(\unicode[STIX]{x1D719}(\mathbf{n}+\mathbf{b}_{i}a_{i},\mathbf{m}+\mathbf{b}_{j}a_{j})+\unicode[STIX]{x1D706}(\mathbf{n}+\mathbf{b}_{i}a_{i})+\unicode[STIX]{x1D707}(\mathbf{m}+\mathbf{b}_{j}a_{j}))|\gg \unicode[STIX]{x1D6FF}.\end{eqnarray}$$
By the pigeonhole principle, we can therefore find
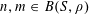 $n,m\in B(S,\unicode[STIX]{x1D70C})$
such that
$n,m\in B(S,\unicode[STIX]{x1D70C})$
such that
 $$\begin{eqnarray}|\mathbb{E}e(\unicode[STIX]{x1D719}(n+\mathbf{b}_{i}a_{i},m+\mathbf{b}_{j}a_{j})+\unicode[STIX]{x1D706}(n+\mathbf{b}_{i}a_{i})+\unicode[STIX]{x1D707}(m+\mathbf{b}_{j}a_{j}))|\gg \unicode[STIX]{x1D6FF}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}e(\unicode[STIX]{x1D719}(n+\mathbf{b}_{i}a_{i},m+\mathbf{b}_{j}a_{j})+\unicode[STIX]{x1D706}(n+\mathbf{b}_{i}a_{i})+\unicode[STIX]{x1D707}(m+\mathbf{b}_{j}a_{j}))|\gg \unicode[STIX]{x1D6FF}.\end{eqnarray}$$
Using the local bilinearity of
![]() $\unicode[STIX]{x1D719}$
, the left-hand side may be written as
$\unicode[STIX]{x1D719}$
, the left-hand side may be written as
 $$\begin{eqnarray}|\mathbb{E}e(\mathbf{b}_{i}\mathbf{b}_{j}\unicode[STIX]{x1D719}(a_{i},a_{j})+\unicode[STIX]{x1D6FC}\mathbf{b}_{i}+\unicode[STIX]{x1D6FD}\mathbf{b}_{j}+\unicode[STIX]{x1D6FE})|\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}e(\mathbf{b}_{i}\mathbf{b}_{j}\unicode[STIX]{x1D719}(a_{i},a_{j})+\unicode[STIX]{x1D6FC}\mathbf{b}_{i}+\unicode[STIX]{x1D6FD}\mathbf{b}_{j}+\unicode[STIX]{x1D6FE})|\end{eqnarray}$$
for some
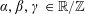 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in \mathbb{R}/\mathbb{Z}$
depending on
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in \mathbb{R}/\mathbb{Z}$
depending on
 $i,j,n,m$
whose exact values are not of importance to us. Evaluating the expectations and using the triangle inequality, we conclude that
$i,j,n,m$
whose exact values are not of importance to us. Evaluating the expectations and using the triangle inequality, we conclude that
 $$\begin{eqnarray}\mathbb{E}_{1\leqslant b_{i}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{i}\unicode[STIX]{x1D70C}/d}|\mathbb{E}_{1\leqslant b_{j}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{j}\unicode[STIX]{x1D70C}/d}e(b_{j}(b_{i}\unicode[STIX]{x1D719}(a_{i},a_{j})+\unicode[STIX]{x1D6FD}))|\gg \unicode[STIX]{x1D6FF}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}_{1\leqslant b_{i}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{i}\unicode[STIX]{x1D70C}/d}|\mathbb{E}_{1\leqslant b_{j}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{j}\unicode[STIX]{x1D70C}/d}e(b_{j}(b_{i}\unicode[STIX]{x1D719}(a_{i},a_{j})+\unicode[STIX]{x1D6FD}))|\gg \unicode[STIX]{x1D6FF}\end{eqnarray}$$
and hence (by Lemma 2.2)
 $$\begin{eqnarray}|\mathbb{E}_{1\leqslant b_{j}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{j}\unicode[STIX]{x1D70C}/d}e(b_{j}(b_{i}\unicode[STIX]{x1D719}(a_{i},a_{j})+\unicode[STIX]{x1D6FD}))|\gg \unicode[STIX]{x1D6FF}\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}_{1\leqslant b_{j}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{j}\unicode[STIX]{x1D70C}/d}e(b_{j}(b_{i}\unicode[STIX]{x1D719}(a_{i},a_{j})+\unicode[STIX]{x1D6FD}))|\gg \unicode[STIX]{x1D6FF}\end{eqnarray}$$
for
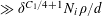 $\gg \unicode[STIX]{x1D6FF}^{C_{1}/4+1}N_{i}\unicode[STIX]{x1D70C}/d$
values of
$\gg \unicode[STIX]{x1D6FF}^{C_{1}/4+1}N_{i}\unicode[STIX]{x1D70C}/d$
values of
![]() $b_{i}$
in the range
$b_{i}$
in the range
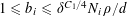 $1\leqslant b_{i}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{i}\unicode[STIX]{x1D70C}/d$
. This average is a geometric series that can be explicitly computed, leading to the bound
$1\leqslant b_{i}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{i}\unicode[STIX]{x1D70C}/d$
. This average is a geometric series that can be explicitly computed, leading to the bound
 $$\begin{eqnarray}\Vert b_{i}\unicode[STIX]{x1D719}(a_{i},a_{j})+\unicode[STIX]{x1D6FD}\Vert _{\mathbb{R}/\mathbb{Z}}\ll \frac{d}{\unicode[STIX]{x1D6FF}^{C_{1}/4+1}N_{j}\unicode[STIX]{x1D70C}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert b_{i}\unicode[STIX]{x1D719}(a_{i},a_{j})+\unicode[STIX]{x1D6FD}\Vert _{\mathbb{R}/\mathbb{Z}}\ll \frac{d}{\unicode[STIX]{x1D6FF}^{C_{1}/4+1}N_{j}\unicode[STIX]{x1D70C}}\end{eqnarray}$$
for
 $\gg \unicode[STIX]{x1D6FF}^{C_{1}/4+1}N_{i}\unicode[STIX]{x1D70C}/d$
values of
$\gg \unicode[STIX]{x1D6FF}^{C_{1}/4+1}N_{i}\unicode[STIX]{x1D70C}/d$
values of
![]() $b_{i}$
in the range
$b_{i}$
in the range
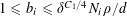 $1\leqslant b_{i}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{i}\unicode[STIX]{x1D70C}/d$
. Applying [Reference Green and Tao17, Lemma A.4] (which is really an observation of Vinogradov, used often in the theory of Weyl sums), we conclude that
$1\leqslant b_{i}\leqslant \unicode[STIX]{x1D6FF}^{C_{1}/4}N_{i}\unicode[STIX]{x1D70C}/d$
. Applying [Reference Green and Tao17, Lemma A.4] (which is really an observation of Vinogradov, used often in the theory of Weyl sums), we conclude that
 $$\begin{eqnarray}\Vert k_{i,j}\unicode[STIX]{x1D719}(a_{i},a_{j})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \frac{d^{2}}{\unicode[STIX]{x1D6FF}^{O(C_{1})}N_{i}N_{j}\unicode[STIX]{x1D70C}^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert k_{i,j}\unicode[STIX]{x1D719}(a_{i},a_{j})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \frac{d^{2}}{\unicode[STIX]{x1D6FF}^{O(C_{1})}N_{i}N_{j}\unicode[STIX]{x1D70C}^{2}}\end{eqnarray}$$
for some natural number
![]() $k_{i,j}$
with
$k_{i,j}$
with
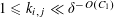 $1\leqslant k_{i,j}\ll \unicode[STIX]{x1D6FF}^{-O(C_{1})}$
. If we then “clear denominators” by defining
$1\leqslant k_{i,j}\ll \unicode[STIX]{x1D6FF}^{-O(C_{1})}$
. If we then “clear denominators” by defining
 $$\begin{eqnarray}k:=\mathop{\prod }_{1\leqslant i,j\leqslant d:N_{i},N_{j}\geqslant d/\unicode[STIX]{x1D6FF}^{C_{1}/2}\unicode[STIX]{x1D70C}}k_{i,j},\end{eqnarray}$$
$$\begin{eqnarray}k:=\mathop{\prod }_{1\leqslant i,j\leqslant d:N_{i},N_{j}\geqslant d/\unicode[STIX]{x1D6FF}^{C_{1}/2}\unicode[STIX]{x1D70C}}k_{i,j},\end{eqnarray}$$
then
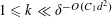 $1\leqslant k\ll \unicode[STIX]{x1D6FF}^{-O(C_{1}d^{2})}$
and
$1\leqslant k\ll \unicode[STIX]{x1D6FF}^{-O(C_{1}d^{2})}$
and
 $$\begin{eqnarray}\Vert k\unicode[STIX]{x1D719}(a_{i},a_{j})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \frac{1}{\unicode[STIX]{x1D6FF}^{O(C_{1}d^{2})}N_{i}N_{j}\unicode[STIX]{x1D70C}^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert k\unicode[STIX]{x1D719}(a_{i},a_{j})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \frac{1}{\unicode[STIX]{x1D6FF}^{O(C_{1}d^{2})}N_{i}N_{j}\unicode[STIX]{x1D70C}^{2}}\end{eqnarray}$$
for all
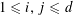 $1\leqslant i,j\leqslant d$
with
$1\leqslant i,j\leqslant d$
with
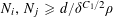 $N_{i},N_{j}\geqslant d/\unicode[STIX]{x1D6FF}^{C_{1}/2}\unicode[STIX]{x1D70C}$
.
$N_{i},N_{j}\geqslant d/\unicode[STIX]{x1D6FF}^{C_{1}/2}\unicode[STIX]{x1D70C}$
.
For any
 $n\in \mathbb{Z}/p\mathbb{Z}$
, we see from Corollary 4.9 that we can find integers
$n\in \mathbb{Z}/p\mathbb{Z}$
, we see from Corollary 4.9 that we can find integers
 $n_{1},\ldots ,n_{d}$
with
$n_{1},\ldots ,n_{d}$
with
 $$\begin{eqnarray}n_{i}\ll (2d)^{O(d)}N_{i}\Vert n\Vert _{S^{\bot }}\end{eqnarray}$$
$$\begin{eqnarray}n_{i}\ll (2d)^{O(d)}N_{i}\Vert n\Vert _{S^{\bot }}\end{eqnarray}$$
such that
 $$\begin{eqnarray}n=n_{1}a_{1}+\cdots +n_{d}a_{d}.\end{eqnarray}$$
$$\begin{eqnarray}n=n_{1}a_{1}+\cdots +n_{d}a_{d}.\end{eqnarray}$$
In particular, if
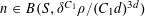 $n\in B(S,\unicode[STIX]{x1D6FF}^{C_{1}}\unicode[STIX]{x1D70C}/(C_{1}d)^{3d})$
, then
$n\in B(S,\unicode[STIX]{x1D6FF}^{C_{1}}\unicode[STIX]{x1D70C}/(C_{1}d)^{3d})$
, then
![]() $n_{i}$
is only non-zero when
$n_{i}$
is only non-zero when
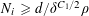 $N_{i}\geqslant d/\unicode[STIX]{x1D6FF}^{C_{1}/2}\unicode[STIX]{x1D70C}$
. From these bounds, (4.20), and the local bilinearity of
$N_{i}\geqslant d/\unicode[STIX]{x1D6FF}^{C_{1}/2}\unicode[STIX]{x1D70C}$
. From these bounds, (4.20), and the local bilinearity of
![]() $\unicode[STIX]{x1D719}$
, we conclude (4.19) as desired.◻
$\unicode[STIX]{x1D719}$
, we conclude (4.19) as desired.◻
Local
 $U^{2}$
-inverse theorem
$U^{2}$
-inverse theorem
The global inverse
![]() $U^{2}$
theorem, which is a simple and well-known exercise in discrete Fourier analysis, asserts that if a
$U^{2}$
theorem, which is a simple and well-known exercise in discrete Fourier analysis, asserts that if a
![]() $1$
-bounded function
$1$
-bounded function
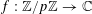 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
obeys the bound
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
obeys the bound
 $$\begin{eqnarray}|\mathbb{E}f(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\geqslant \unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\geqslant \unicode[STIX]{x1D702}\end{eqnarray}$$
where
 $\mathbf{h}_{0},\mathbf{h}_{1},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1}^{\prime }$
are drawn uniformly at random from
$\mathbf{h}_{0},\mathbf{h}_{1},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1}^{\prime }$
are drawn uniformly at random from
![]() $\mathbb{Z}/p\mathbb{Z}$
, then there exists
$\mathbb{Z}/p\mathbb{Z}$
, then there exists
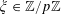 $\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}|\mathbb{E}f(\mathbf{h})e_{p}(-\unicode[STIX]{x1D709}\mathbf{h})|\geqslant \unicode[STIX]{x1D702}^{1/2}\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f(\mathbf{h})e_{p}(-\unicode[STIX]{x1D709}\mathbf{h})|\geqslant \unicode[STIX]{x1D702}^{1/2}\end{eqnarray}$$
where
![]() $\mathbf{h}$
is also drawn uniformly at random from
$\mathbf{h}$
is also drawn uniformly at random from
![]() $\mathbb{Z}/p\mathbb{Z}$
.
$\mathbb{Z}/p\mathbb{Z}$
.
In this section we give a local version of the above claim, in which the random variables
 $\mathbf{h},\mathbf{h}_{0},\mathbf{h}_{1},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1}^{\prime }$
are localized to a small Bohr set. If the rank of the Bohr set is bounded, one can modify the above arguments to obtain a reasonable inverse theorem of this nature, but in our application the rank of the Bohr set will be rather large, and it will be important that this rank does not affect the lower bound in correlations of the form (4.22). Fortunately, such a result is available, and will be crucial in the proofs of the two remaining claims (Corollary 4.13 and Theorem 8.1) needed to prove Theorem 1.1.
$\mathbf{h},\mathbf{h}_{0},\mathbf{h}_{1},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1}^{\prime }$
are localized to a small Bohr set. If the rank of the Bohr set is bounded, one can modify the above arguments to obtain a reasonable inverse theorem of this nature, but in our application the rank of the Bohr set will be rather large, and it will be important that this rank does not affect the lower bound in correlations of the form (4.22). Fortunately, such a result is available, and will be crucial in the proofs of the two remaining claims (Corollary 4.13 and Theorem 8.1) needed to prove Theorem 1.1.
Here is a precise version of the claim.
Theorem 4.12. Let
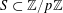 $S\subset \mathbb{Z}/p\mathbb{Z}$
be non-degenerate for some prime
$S\subset \mathbb{Z}/p\mathbb{Z}$
be non-degenerate for some prime
![]() $p$
, and let
$p$
, and let
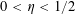 $0<\unicode[STIX]{x1D702}<1/2$
. Let
$0<\unicode[STIX]{x1D702}<1/2$
. Let
![]() $\unicode[STIX]{x1D70C}_{0},\unicode[STIX]{x1D70C}_{1}$
be real parameters with
$\unicode[STIX]{x1D70C}_{0},\unicode[STIX]{x1D70C}_{1}$
be real parameters with
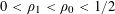 $0<\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{0}<1/2$
and such that
$0<\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{0}<1/2$
and such that
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{0}>\frac{C|S|}{\unicode[STIX]{x1D702}^{2}}\unicode[STIX]{x1D70C}_{1}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{0}>\frac{C|S|}{\unicode[STIX]{x1D702}^{2}}\unicode[STIX]{x1D70C}_{1}\end{eqnarray}$$
for a sufficiently large absolute constant
![]() $C$
. Let
$C$
. Let
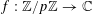 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
be a
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
be a
![]() $1$
-bounded function such that
$1$
-bounded function such that
 $$\begin{eqnarray}|\mathbb{E}f(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\geqslant \unicode[STIX]{x1D702},\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\geqslant \unicode[STIX]{x1D702},\end{eqnarray}$$
where
 $\mathbf{h}_{0},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1},\mathbf{h}_{1}^{\prime }$
are drawn independently and regularly from
$\mathbf{h}_{0},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1},\mathbf{h}_{1}^{\prime }$
are drawn independently and regularly from
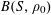 $B(S,\unicode[STIX]{x1D70C}_{0})$
,
$B(S,\unicode[STIX]{x1D70C}_{0})$
,
 $B(S,\unicode[STIX]{x1D70C}_{0})$
,
$B(S,\unicode[STIX]{x1D70C}_{0})$
,
 $B(S,\unicode[STIX]{x1D70C}_{1})$
,
$B(S,\unicode[STIX]{x1D70C}_{1})$
,
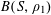 $B(S,\unicode[STIX]{x1D70C}_{1})$
respectively. Then there exists
$B(S,\unicode[STIX]{x1D70C}_{1})$
respectively. Then there exists
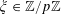 $\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}\mathbf{n}_{1})|^{2}\geqslant \unicode[STIX]{x1D702}/2\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}\mathbf{n}_{1})|^{2}\geqslant \unicode[STIX]{x1D702}/2\end{eqnarray}$$
where
![]() $\mathbf{n}_{0},\mathbf{n}_{1}$
are drawn independently and regularly from
$\mathbf{n}_{0},\mathbf{n}_{1}$
are drawn independently and regularly from
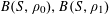 $B(S,\unicode[STIX]{x1D70C}_{0}),B(S,\unicode[STIX]{x1D70C}_{1})$
respectively.
$B(S,\unicode[STIX]{x1D70C}_{0}),B(S,\unicode[STIX]{x1D70C}_{1})$
respectively.
Proof. We thank Fernando Shao for supplying a proof of this result, which was considerably simpler than our original argument.
For this proof, which is Fourier-analytic in nature, it will be convenient to work explicitly with probability densities rather than probabilistic notation. (However, in the lengthier proof of the local inverse
![]() $U^{3}$
theorem given in the next section, the probabilistic notation will be significantly cleaner to use.) In this argument, all sums will be over
$U^{3}$
theorem given in the next section, the probabilistic notation will be significantly cleaner to use.) In this argument, all sums will be over
![]() $\mathbb{Z}/p\mathbb{Z}$
. We abbreviate
$\mathbb{Z}/p\mathbb{Z}$
. We abbreviate
 $$\begin{eqnarray}\mathfrak{p}_{i}(h):=\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C}_{i})}(h)=\mathbb{P}(\mathbf{h}_{i}=h)\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}_{i}(h):=\mathfrak{p}_{B(S,\unicode[STIX]{x1D70C}_{i})}(h)=\mathbb{P}(\mathbf{h}_{i}=h)\end{eqnarray}$$
for
![]() $i=0,1$
and
$i=0,1$
and
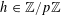 $h\in \mathbb{Z}/p\mathbb{Z}$
; clearly we have
$h\in \mathbb{Z}/p\mathbb{Z}$
; clearly we have
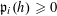 $\mathfrak{p}_{i}(h)\geqslant 0$
and
$\mathfrak{p}_{i}(h)\geqslant 0$
and
 $$\begin{eqnarray}\mathop{\sum }_{h}\mathfrak{p}_{i}(h)=1.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{h}\mathfrak{p}_{i}(h)=1.\end{eqnarray}$$
The hypothesis (4.24) may be written as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}\mathfrak{p}_{0}(h_{0})\mathfrak{p}_{0}(h_{0}^{\prime })\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })f(h_{0}+h_{1})\overline{f}(h_{0}+h_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(h_{0}^{\prime }+h_{1})f(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\geqslant \unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}\mathfrak{p}_{0}(h_{0})\mathfrak{p}_{0}(h_{0}^{\prime })\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })f(h_{0}+h_{1})\overline{f}(h_{0}+h_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(h_{0}^{\prime }+h_{1})f(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\geqslant \unicode[STIX]{x1D702}\end{eqnarray}$$
and our goal is to locate
 $\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}}\mathfrak{p}_{0}(n_{0})\biggl|\mathop{\sum }_{n_{1}}\mathfrak{p}_{1}(n_{1})f(n_{0}+n_{1})e_{p}(-\unicode[STIX]{x1D709}n_{1})\biggr|^{2}\geqslant \unicode[STIX]{x1D702}/2.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}}\mathfrak{p}_{0}(n_{0})\biggl|\mathop{\sum }_{n_{1}}\mathfrak{p}_{1}(n_{1})f(n_{0}+n_{1})e_{p}(-\unicode[STIX]{x1D709}n_{1})\biggr|^{2}\geqslant \unicode[STIX]{x1D702}/2.\end{eqnarray}$$
The first step is to replace the factor
![]() $\mathfrak{p}_{0}(h_{0})$
by the slightly different factor
$\mathfrak{p}_{0}(h_{0})$
by the slightly different factor
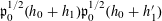 $\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1}^{\prime })$
. If we use the elementary inequality
$\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1}^{\prime })$
. If we use the elementary inequality
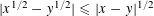 $|x^{1/2}-y^{1/2}|\leqslant |x-y|^{1/2}$
for
$|x^{1/2}-y^{1/2}|\leqslant |x-y|^{1/2}$
for
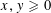 $x,y\geqslant 0$
and then apply Cauchy–Schwarz, Lemma 4.4, and (4.23), we see that
$x,y\geqslant 0$
and then apply Cauchy–Schwarz, Lemma 4.4, and (4.23), we see that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{h_{0}}|\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})-\mathfrak{p}_{0}^{1/2}(h_{0})|\mathfrak{p}_{0}^{1/2}(h_{0})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{h_{0}}|\mathfrak{p}_{0}(h_{0}+h_{1})-\mathfrak{p}_{0}(h_{0})|^{1/2}\mathfrak{p}_{0}^{1/2}(h_{0})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \biggl(\mathop{\sum }_{h_{0}\in \mathbb{Z}/p\mathbb{Z}}|\mathfrak{p}_{0}(h_{0}+h_{1})-\mathfrak{p}_{0}(h_{0})|\biggr)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl(\mathop{\sum }_{h_{0}\in \mathbb{Z}/p\mathbb{Z}}b_{h_{1}}(h_{0})\mathfrak{p}_{0}(h_{0}+h_{1})-b_{h_{1}}(h_{0})\mathfrak{p}_{0}(h_{0})\biggr)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \biggl(\frac{|S|\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x1D70C}_{0}}\biggr)^{1/2}\ll \frac{\unicode[STIX]{x1D702}}{C^{1/2}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{h_{0}}|\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})-\mathfrak{p}_{0}^{1/2}(h_{0})|\mathfrak{p}_{0}^{1/2}(h_{0})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{h_{0}}|\mathfrak{p}_{0}(h_{0}+h_{1})-\mathfrak{p}_{0}(h_{0})|^{1/2}\mathfrak{p}_{0}^{1/2}(h_{0})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \biggl(\mathop{\sum }_{h_{0}\in \mathbb{Z}/p\mathbb{Z}}|\mathfrak{p}_{0}(h_{0}+h_{1})-\mathfrak{p}_{0}(h_{0})|\biggr)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl(\mathop{\sum }_{h_{0}\in \mathbb{Z}/p\mathbb{Z}}b_{h_{1}}(h_{0})\mathfrak{p}_{0}(h_{0}+h_{1})-b_{h_{1}}(h_{0})\mathfrak{p}_{0}(h_{0})\biggr)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \ll \biggl(\frac{|S|\unicode[STIX]{x1D70C}_{1}}{\unicode[STIX]{x1D70C}_{0}}\biggr)^{1/2}\ll \frac{\unicode[STIX]{x1D702}}{C^{1/2}}\nonumber\end{eqnarray}$$
for any
![]() $h_{1}$
in the support of
$h_{1}$
in the support of
![]() $\mathfrak{p}_{1}$
, where the
$\mathfrak{p}_{1}$
, where the
![]() $1$
-bounded function
$1$
-bounded function
![]() $b_{h_{1}}$
is given by
$b_{h_{1}}$
is given by
 $b_{h_{1}}(h_{0}):=\operatorname{sgn}(\mathfrak{p}_{0}(h_{0}+h_{1})-\mathfrak{p}_{0}(h_{0}))$
. Similarly we have
$b_{h_{1}}(h_{0}):=\operatorname{sgn}(\mathfrak{p}_{0}(h_{0}+h_{1})-\mathfrak{p}_{0}(h_{0}))$
. Similarly we have
 $$\begin{eqnarray}\mathop{\sum }_{h_{0}}|\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1}^{\prime })-\mathfrak{p}_{0}^{1/2}(h_{0})|\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})\ll \frac{\unicode[STIX]{x1D702}}{C^{1/2}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{h_{0}}|\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1}^{\prime })-\mathfrak{p}_{0}^{1/2}(h_{0})|\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})\ll \frac{\unicode[STIX]{x1D702}}{C^{1/2}}\end{eqnarray}$$
whenever
![]() $h_{1}^{\prime }$
is also in the support of
$h_{1}^{\prime }$
is also in the support of
![]() $\mathfrak{p}_{1}$
; by the triangle inequality, we conclude that
$\mathfrak{p}_{1}$
; by the triangle inequality, we conclude that
 $$\begin{eqnarray}\mathop{\sum }_{h_{0}}|\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})\mathfrak{p}_{0}(h_{0}+h_{1}^{\prime })^{1/2}-\mathfrak{p}_{0}(h_{0})|\ll \frac{\unicode[STIX]{x1D702}}{C^{1/2}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{h_{0}}|\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})\mathfrak{p}_{0}(h_{0}+h_{1}^{\prime })^{1/2}-\mathfrak{p}_{0}(h_{0})|\ll \frac{\unicode[STIX]{x1D702}}{C^{1/2}}\end{eqnarray}$$
for all
![]() $h_{1},h_{1}^{\prime }$
in the support of
$h_{1},h_{1}^{\prime }$
in the support of
![]() $\mathfrak{p}_{1}$
. From the
$\mathfrak{p}_{1}$
. From the
![]() $1$
-boundedness of
$1$
-boundedness of
![]() $f$
and (4.25), we conclude that
$f$
and (4.25), we conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}|\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1}^{\prime })-\mathfrak{p}_{0}(h_{0})|\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathfrak{p}_{0}(h_{0}^{\prime })\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })f(h_{0}+h_{1})\overline{f}(h_{0}+h_{1}^{\prime })\overline{f}(h_{0}^{\prime }+h_{1})f(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \ll \frac{\unicode[STIX]{x1D702}}{C^{1/2}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}|\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1}^{\prime })-\mathfrak{p}_{0}(h_{0})|\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathfrak{p}_{0}(h_{0}^{\prime })\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })f(h_{0}+h_{1})\overline{f}(h_{0}+h_{1}^{\prime })\overline{f}(h_{0}^{\prime }+h_{1})f(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \ll \frac{\unicode[STIX]{x1D702}}{C^{1/2}}.\nonumber\end{eqnarray}$$
If
![]() $C$
is large enough, the left-hand side is thus bounded by
$C$
is large enough, the left-hand side is thus bounded by
![]() $0.1\unicode[STIX]{x1D702}$
(for example), so by (4.26) and the triangle inequality we conclude that
$0.1\unicode[STIX]{x1D702}$
(for example), so by (4.26) and the triangle inequality we conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1}^{\prime })\mathfrak{p}_{0}(h_{0}^{\prime })\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f(h_{0}+h_{1})\overline{f}(h_{0}+h_{1}^{\prime })\overline{f}(h_{0}^{\prime }+h_{1})f(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\geqslant 0.9\unicode[STIX]{x1D702}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1})\mathfrak{p}_{0}^{1/2}(h_{0}+h_{1}^{\prime })\mathfrak{p}_{0}(h_{0}^{\prime })\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f(h_{0}+h_{1})\overline{f}(h_{0}+h_{1}^{\prime })\overline{f}(h_{0}^{\prime }+h_{1})f(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\geqslant 0.9\unicode[STIX]{x1D702}\nonumber\end{eqnarray}$$
If we write
 $$\begin{eqnarray}f_{0}(n):=f(n)\mathfrak{p}_{0}^{1/2}(n),\end{eqnarray}$$
$$\begin{eqnarray}f_{0}(n):=f(n)\mathfrak{p}_{0}^{1/2}(n),\end{eqnarray}$$
we may rewrite the above estimate as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}\mathfrak{p}_{0}(h_{0}^{\prime })\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{0}(h_{0}+h_{1})\overline{f_{0}}(h_{0}+h_{1}^{\prime })\overline{f}(h_{0}^{\prime }+h_{1})f(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\geqslant 0.9\unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}\mathfrak{p}_{0}(h_{0}^{\prime })\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{0}(h_{0}+h_{1})\overline{f_{0}}(h_{0}+h_{1}^{\prime })\overline{f}(h_{0}^{\prime }+h_{1})f(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\geqslant 0.9\unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
A similar argument then lets us replace
![]() $\mathfrak{p}_{0}(h_{0}^{\prime })$
with
$\mathfrak{p}_{0}(h_{0}^{\prime })$
with
 $\mathfrak{p}_{0}^{1/2}(h_{0}^{\prime }+h_{1})\mathfrak{p}_{0}^{1/2}(h_{0}^{\prime }+h_{1}^{\prime })$
, leaving us with
$\mathfrak{p}_{0}^{1/2}(h_{0}^{\prime }+h_{1})\mathfrak{p}_{0}^{1/2}(h_{0}^{\prime }+h_{1}^{\prime })$
, leaving us with
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}\mathfrak{p}_{0}(h_{0}^{\prime }+h_{1})^{1/2}\mathfrak{p}_{0}(h_{0}^{\prime }+h_{1}^{\prime })^{1/2}\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{0}(h_{0}+h_{1})\overline{f_{0}}(h_{0}+h_{1}^{\prime })\overline{f}(h_{0}^{\prime }+h_{1})f(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\geqslant 0.8\unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}\mathfrak{p}_{0}(h_{0}^{\prime }+h_{1})^{1/2}\mathfrak{p}_{0}(h_{0}^{\prime }+h_{1}^{\prime })^{1/2}\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{0}(h_{0}+h_{1})\overline{f_{0}}(h_{0}+h_{1}^{\prime })\overline{f}(h_{0}^{\prime }+h_{1})f(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\geqslant 0.8\unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
which we can simplify using (4.27) to
 $$\begin{eqnarray}\biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })f_{0}(h_{0}+h_{1})\overline{f_{0}}(h_{0}+h_{1}^{\prime })\overline{f_{0}}(h_{0}^{\prime }+h_{1})f_{0}(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\geqslant 0.8\unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathop{\sum }_{h_{0},h_{0}^{\prime },h_{1},h_{1}^{\prime }}\mathfrak{p}_{1}(h_{1})\mathfrak{p}_{1}(h_{1}^{\prime })f_{0}(h_{0}+h_{1})\overline{f_{0}}(h_{0}+h_{1}^{\prime })\overline{f_{0}}(h_{0}^{\prime }+h_{1})f_{0}(h_{0}^{\prime }+h_{1}^{\prime })\biggr|\geqslant 0.8\unicode[STIX]{x1D702}.\end{eqnarray}$$
Making the change of variables
 $n:=h_{1}-h_{1}^{\prime }$
, we may rewrite the left-hand side as
$n:=h_{1}-h_{1}^{\prime }$
, we may rewrite the left-hand side as
 $$\begin{eqnarray}\mathop{\sum }_{n}(\mathfrak{p}_{1}\ast \tilde{\mathfrak{p}}_{1})(n)|(f_{0}\ast \tilde{f}_{0})(n)|^{2}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n}(\mathfrak{p}_{1}\ast \tilde{\mathfrak{p}}_{1})(n)|(f_{0}\ast \tilde{f}_{0})(n)|^{2}\end{eqnarray}$$
where
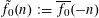 $\tilde{f}_{0}(n):=\overline{f_{0}}(-n)$
, and similarly for
$\tilde{f}_{0}(n):=\overline{f_{0}}(-n)$
, and similarly for
![]() $p_{1}$
, and
$p_{1}$
, and
![]() $f\ast g$
denotes the discrete convolution
$f\ast g$
denotes the discrete convolution
 $$\begin{eqnarray}f\ast g(n):=\mathop{\sum }_{m}f(m)g(n-m).\end{eqnarray}$$
$$\begin{eqnarray}f\ast g(n):=\mathop{\sum }_{m}f(m)g(n-m).\end{eqnarray}$$
Using the Fourier transform, we may then rewrite the previous bound as
 $$\begin{eqnarray}p^{4}\mathop{\sum }_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime }}|\hat{\mathfrak{p}}_{1}(\unicode[STIX]{x1D709}^{\prime })|^{2}|\hat{f}_{0}(\unicode[STIX]{x1D709})|^{2}|\hat{f}_{0}(\unicode[STIX]{x1D709}+\unicode[STIX]{x1D709}^{\prime })|^{2}\geqslant 0.8\unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}p^{4}\mathop{\sum }_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime }}|\hat{\mathfrak{p}}_{1}(\unicode[STIX]{x1D709}^{\prime })|^{2}|\hat{f}_{0}(\unicode[STIX]{x1D709})|^{2}|\hat{f}_{0}(\unicode[STIX]{x1D709}+\unicode[STIX]{x1D709}^{\prime })|^{2}\geqslant 0.8\unicode[STIX]{x1D702}\end{eqnarray}$$
where
 $$\begin{eqnarray}\hat{f}(\unicode[STIX]{x1D709}):=\frac{1}{p}\mathop{\sum }_{n}f(n)e_{p}(-\unicode[STIX]{x1D709}n).\end{eqnarray}$$
$$\begin{eqnarray}\hat{f}(\unicode[STIX]{x1D709}):=\frac{1}{p}\mathop{\sum }_{n}f(n)e_{p}(-\unicode[STIX]{x1D709}n).\end{eqnarray}$$
From (4.25), the
![]() $1$
-boundedness of
$1$
-boundedness of
![]() $f$
, and the Plancherel identity we have
$f$
, and the Plancherel identity we have
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D709}}|\hat{f}_{0}(\unicode[STIX]{x1D709})|^{2}=\frac{1}{p}\mathop{\sum }_{n}|f_{0}(n)|^{2}\leqslant \frac{1}{p}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D709}}|\hat{f}_{0}(\unicode[STIX]{x1D709})|^{2}=\frac{1}{p}\mathop{\sum }_{n}|f_{0}(n)|^{2}\leqslant \frac{1}{p}.\end{eqnarray}$$
By this, (4.28), and the pigeonhole principle, we may therefore find
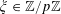 $\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}p^{3}\mathop{\sum }_{\unicode[STIX]{x1D709}^{\prime }\in \mathbb{Z}/p\mathbb{Z}}|\hat{p}_{1}(\unicode[STIX]{x1D709}^{\prime })|^{2}|\hat{f}_{0}(\unicode[STIX]{x1D709}+\unicode[STIX]{x1D709}^{\prime })|^{2}\geqslant 0.8\unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}p^{3}\mathop{\sum }_{\unicode[STIX]{x1D709}^{\prime }\in \mathbb{Z}/p\mathbb{Z}}|\hat{p}_{1}(\unicode[STIX]{x1D709}^{\prime })|^{2}|\hat{f}_{0}(\unicode[STIX]{x1D709}+\unicode[STIX]{x1D709}^{\prime })|^{2}\geqslant 0.8\unicode[STIX]{x1D702}.\end{eqnarray}$$
By the Plancherel identity again, the left-hand side may be rewritten as
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}}\biggl|\mathop{\sum }_{n_{1}}f_{0}(n_{0}-n_{1})\mathfrak{p}_{1}(n_{1})e_{p}(\unicode[STIX]{x1D709}n_{1})\biggr|^{2}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}}\biggl|\mathop{\sum }_{n_{1}}f_{0}(n_{0}-n_{1})\mathfrak{p}_{1}(n_{1})e_{p}(\unicode[STIX]{x1D709}n_{1})\biggr|^{2}\end{eqnarray}$$
and hence (by replacing
![]() $n_{1}$
with
$n_{1}$
with
![]() $-n_{1}$
and using (4.27))
$-n_{1}$
and using (4.27))
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}}\biggl|\mathop{\sum }_{n_{1}}f(n_{0}+n_{1})\mathfrak{p}_{0}^{1/2}(n_{0}+n_{1})\mathfrak{p}_{1}(n_{1})e_{p}(-\unicode[STIX]{x1D709}n_{1})\biggr|^{2}\geqslant 0.8\unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}}\biggl|\mathop{\sum }_{n_{1}}f(n_{0}+n_{1})\mathfrak{p}_{0}^{1/2}(n_{0}+n_{1})\mathfrak{p}_{1}(n_{1})e_{p}(-\unicode[STIX]{x1D709}n_{1})\biggr|^{2}\geqslant 0.8\unicode[STIX]{x1D702}.\end{eqnarray}$$
By argument similar to those at the beginning of the proof, we may replace
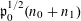 $\mathfrak{p}_{0}^{1/2}(n_{0}+n_{1})$
by
$\mathfrak{p}_{0}^{1/2}(n_{0}+n_{1})$
by
![]() $\mathfrak{p}_{0}^{1/2}(n_{0})$
and conclude that
$\mathfrak{p}_{0}^{1/2}(n_{0})$
and conclude that
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}}\biggl|\mathop{\sum }_{n_{1}}f(n_{0}+n_{1})\mathfrak{p}_{0}^{1/2}(n_{0})\mathfrak{p}_{1}(n_{1})e(-\unicode[STIX]{x1D709}n_{1})\biggr|^{2}\geqslant 0.7\unicode[STIX]{x1D702},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}}\biggl|\mathop{\sum }_{n_{1}}f(n_{0}+n_{1})\mathfrak{p}_{0}^{1/2}(n_{0})\mathfrak{p}_{1}(n_{1})e(-\unicode[STIX]{x1D709}n_{1})\biggr|^{2}\geqslant 0.7\unicode[STIX]{x1D702},\end{eqnarray}$$
and the claim follows. ◻
As a corollary of this inverse theorem, we can establish that locally almost linear phases on Bohr sets can be approximated by globally linear phases; this will be needed in §7 to deal with poorly distributed quadratic factors.
Here is a precise statement.
Corollary 4.13. Let
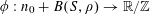 $\unicode[STIX]{x1D719}:n_{0}+B(S,\unicode[STIX]{x1D70C})\rightarrow \mathbb{R}/\mathbb{Z}$
be a function on a shifted Bohr set
$\unicode[STIX]{x1D719}:n_{0}+B(S,\unicode[STIX]{x1D70C})\rightarrow \mathbb{R}/\mathbb{Z}$
be a function on a shifted Bohr set
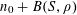 $n_{0}+B(S,\unicode[STIX]{x1D70C})$
that is “locally almost linear” in the sense that one has the bound
$n_{0}+B(S,\unicode[STIX]{x1D70C})$
that is “locally almost linear” in the sense that one has the bound
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D719}(n_{0}+h+k)-\unicode[STIX]{x1D719}(n_{0}+h)-\unicode[STIX]{x1D719}(n_{0}+k)+\unicode[STIX]{x1D719}(n_{0})\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant A\frac{\Vert h\Vert _{S^{\bot }}\Vert k\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}^{2}}\quad\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D719}(n_{0}+h+k)-\unicode[STIX]{x1D719}(n_{0}+h)-\unicode[STIX]{x1D719}(n_{0}+k)+\unicode[STIX]{x1D719}(n_{0})\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant A\frac{\Vert h\Vert _{S^{\bot }}\Vert k\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}^{2}}\quad\end{eqnarray}$$
for all
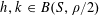 $h,k\in B(S,\unicode[STIX]{x1D70C}/2)$
and some
$h,k\in B(S,\unicode[STIX]{x1D70C}/2)$
and some
![]() $A\geqslant 1$
. Then there exists
$A\geqslant 1$
. Then there exists
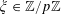 $\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\biggl\|\unicode[STIX]{x1D719}(n_{0}+h)-\unicode[STIX]{x1D719}(n_{0})-\frac{\unicode[STIX]{x1D709}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\ll A^{1/2}|S|^{4}\frac{\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}}\end{eqnarray}$$
$$\begin{eqnarray}\biggl\|\unicode[STIX]{x1D719}(n_{0}+h)-\unicode[STIX]{x1D719}(n_{0})-\frac{\unicode[STIX]{x1D709}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\ll A^{1/2}|S|^{4}\frac{\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}}\end{eqnarray}$$
for all
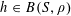 $h\in B(S,\unicode[STIX]{x1D70C})$
.
$h\in B(S,\unicode[STIX]{x1D70C})$
.
Proof. By translating in space, we may normalize so that
![]() $n_{0}=0$
; by shifting
$n_{0}=0$
; by shifting
![]() $\unicode[STIX]{x1D719}$
by a phase, we may also suppose that
$\unicode[STIX]{x1D719}$
by a phase, we may also suppose that
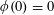 $\unicode[STIX]{x1D719}(0)=0$
. By replacing
$\unicode[STIX]{x1D719}(0)=0$
. By replacing
![]() $\unicode[STIX]{x1D70C}$
with the smaller quantity
$\unicode[STIX]{x1D70C}$
with the smaller quantity
![]() $\unicode[STIX]{x1D70C}/A^{1/2}$
if necessary, we may normalize
$\unicode[STIX]{x1D70C}/A^{1/2}$
if necessary, we may normalize
![]() $A$
to be
$A$
to be
![]() $1$
(note that (4.30) is trivial for
$1$
(note that (4.30) is trivial for
 $\Vert h\Vert _{S^{\bot }}\,\geqslant \,\unicode[STIX]{x1D70C}/A^{1/2}$
). Thus, we now have a function
$\Vert h\Vert _{S^{\bot }}\,\geqslant \,\unicode[STIX]{x1D70C}/A^{1/2}$
). Thus, we now have a function
 $\unicode[STIX]{x1D719}\,:\,B(S,\unicode[STIX]{x1D70C})\rightarrow \mathbb{R}/\mathbb{Z}$
with
$\unicode[STIX]{x1D719}\,:\,B(S,\unicode[STIX]{x1D70C})\rightarrow \mathbb{R}/\mathbb{Z}$
with
 $\unicode[STIX]{x1D719}(0)=0$
such that the quantity
$\unicode[STIX]{x1D719}(0)=0$
such that the quantity
 $$\begin{eqnarray}\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(h,k):=\unicode[STIX]{x1D719}(h+k)-\unicode[STIX]{x1D719}(h)-\unicode[STIX]{x1D719}(k)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(h,k):=\unicode[STIX]{x1D719}(h+k)-\unicode[STIX]{x1D719}(h)-\unicode[STIX]{x1D719}(k)\end{eqnarray}$$
obeys the bound
 $$\begin{eqnarray}\Vert \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(h,k)\Vert _{\mathbb{ R}/\mathbb{Z}}\leqslant \frac{\Vert h\Vert _{S^{\bot }}\Vert k\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(h,k)\Vert _{\mathbb{ R}/\mathbb{Z}}\leqslant \frac{\Vert h\Vert _{S^{\bot }}\Vert k\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}^{2}}\end{eqnarray}$$
for all
 $h,k\in B(S,\unicode[STIX]{x1D70C}/2)$
, and our task is to locate
$h,k\in B(S,\unicode[STIX]{x1D70C}/2)$
, and our task is to locate
 $\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\biggl\|\unicode[STIX]{x1D719}(h)-\frac{\unicode[STIX]{x1D709}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\ll |S|^{4}\frac{\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}}\end{eqnarray}$$
$$\begin{eqnarray}\biggl\|\unicode[STIX]{x1D719}(h)-\frac{\unicode[STIX]{x1D709}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\ll |S|^{4}\frac{\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}}\end{eqnarray}$$
for all
 $h\in B(S,\unicode[STIX]{x1D70C})$
.
$h\in B(S,\unicode[STIX]{x1D70C})$
.
Let
 $\unicode[STIX]{x1D70C}_{0}:=\unicode[STIX]{x1D70C}/100$
, and set
$\unicode[STIX]{x1D70C}_{0}:=\unicode[STIX]{x1D70C}/100$
, and set
 $\unicode[STIX]{x1D70C}_{1}:=\unicode[STIX]{x1D70C}/C|S|^{3}$
for some sufficiently large absolute constant
$\unicode[STIX]{x1D70C}_{1}:=\unicode[STIX]{x1D70C}/C|S|^{3}$
for some sufficiently large absolute constant
![]() $C$
. If we let
$C$
. If we let
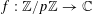 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
be the
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
be the
![]() $1$
-bounded function
$1$
-bounded function
 $$\begin{eqnarray}f(x):=1_{B(S,\unicode[STIX]{x1D70C})}e(\unicode[STIX]{x1D719}(x))\end{eqnarray}$$
$$\begin{eqnarray}f(x):=1_{B(S,\unicode[STIX]{x1D70C})}e(\unicode[STIX]{x1D719}(x))\end{eqnarray}$$
and draw
 $\mathbf{h}_{0},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1},\mathbf{h}_{1}^{\prime }$
independently and regularly from
$\mathbf{h}_{0},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1},\mathbf{h}_{1}^{\prime }$
independently and regularly from
 $B(S,\unicode[STIX]{x1D70C}_{0})$
,
$B(S,\unicode[STIX]{x1D70C}_{0})$
,
 $B(S,\unicode[STIX]{x1D70C}_{0})$
,
$B(S,\unicode[STIX]{x1D70C}_{0})$
,
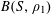 $B(S,\unicode[STIX]{x1D70C}_{1})$
,
$B(S,\unicode[STIX]{x1D70C}_{1})$
,
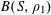 $B(S,\unicode[STIX]{x1D70C}_{1})$
respectively, then from (4.31) we have
$B(S,\unicode[STIX]{x1D70C}_{1})$
respectively, then from (4.31) we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle f(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad =e(\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(\mathbf{h}_{0},\mathbf{h}_{1})-\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(\mathbf{h}_{0}^{\prime },\mathbf{h}_{1})-\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(\mathbf{h}_{0},\mathbf{h}_{1}^{\prime })+\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(\mathbf{h}_{0}^{\prime },\mathbf{h}_{1}^{\prime })).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle f(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad =e(\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(\mathbf{h}_{0},\mathbf{h}_{1})-\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(\mathbf{h}_{0}^{\prime },\mathbf{h}_{1})-\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(\mathbf{h}_{0},\mathbf{h}_{1}^{\prime })+\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(\mathbf{h}_{0}^{\prime },\mathbf{h}_{1}^{\prime })).\nonumber\end{eqnarray}$$
Applying (4.32) and taking expectations, we conclude that
 $$\begin{eqnarray}|\mathbb{E}f(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\geqslant 1/2\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\geqslant 1/2\end{eqnarray}$$
(for example). Applying Theorem 4.12 (which is applicable for
![]() $C$
large enough), we may thus find
$C$
large enough), we may thus find
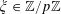 $\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}\mathbf{n}_{1})|^{2}\geqslant 1/4\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}\mathbf{n}_{1})|^{2}\geqslant 1/4\end{eqnarray}$$
if
![]() $\mathbf{n}_{0},\mathbf{n}_{1}$
are drawn independently and regularly from
$\mathbf{n}_{0},\mathbf{n}_{1}$
are drawn independently and regularly from
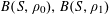 $B(S,\unicode[STIX]{x1D70C}_{0}),B(S,\unicode[STIX]{x1D70C}_{1})$
respectively. In particular, there exists
$B(S,\unicode[STIX]{x1D70C}_{0}),B(S,\unicode[STIX]{x1D70C}_{1})$
respectively. In particular, there exists
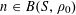 $n\in B(S,\unicode[STIX]{x1D70C}_{0})$
such that
$n\in B(S,\unicode[STIX]{x1D70C}_{0})$
such that
 $$\begin{eqnarray}|\mathbb{E}f(n+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}\mathbf{n}_{1})|\geqslant 1/4.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f(n+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}\mathbf{n}_{1})|\geqslant 1/4.\end{eqnarray}$$
 $$\begin{eqnarray}f(n+\mathbf{n}_{1})=e(\unicode[STIX]{x1D719}(\mathbf{n}_{1})+\unicode[STIX]{x1D719}(n)+\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(n,\mathbf{n}_{1}))\end{eqnarray}$$
$$\begin{eqnarray}f(n+\mathbf{n}_{1})=e(\unicode[STIX]{x1D719}(\mathbf{n}_{1})+\unicode[STIX]{x1D719}(n)+\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(n,\mathbf{n}_{1}))\end{eqnarray}$$
so by (4.32) we conclude that
 $$\begin{eqnarray}\biggl|\mathbb{E}e\biggl(\unicode[STIX]{x1D719}(\mathbf{n}_{1})-\frac{\unicode[STIX]{x1D709}\mathbf{n}_{1}}{p}\biggr)\biggr|\gg 1.\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathbb{E}e\biggl(\unicode[STIX]{x1D719}(\mathbf{n}_{1})-\frac{\unicode[STIX]{x1D709}\mathbf{n}_{1}}{p}\biggr)\biggr|\gg 1.\end{eqnarray}$$
For any
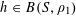 $h\in B(S,\unicode[STIX]{x1D70C}_{1})$
, we have from Lemma 4.4 that
$h\in B(S,\unicode[STIX]{x1D70C}_{1})$
, we have from Lemma 4.4 that
 $$\begin{eqnarray}\biggl|\mathbb{E}e\biggl(\unicode[STIX]{x1D719}(\mathbf{n}_{1}+h)-\frac{\unicode[STIX]{x1D709}(\mathbf{n}_{1}+h)}{p}\biggr)-\mathbb{E}e\biggl(\unicode[STIX]{x1D719}(\mathbf{n}_{1})-\frac{\unicode[STIX]{x1D709}\mathbf{n}_{1}}{p}\biggr)\biggr|\ll |S|\frac{\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}_{1}};\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathbb{E}e\biggl(\unicode[STIX]{x1D719}(\mathbf{n}_{1}+h)-\frac{\unicode[STIX]{x1D709}(\mathbf{n}_{1}+h)}{p}\biggr)-\mathbb{E}e\biggl(\unicode[STIX]{x1D719}(\mathbf{n}_{1})-\frac{\unicode[STIX]{x1D709}\mathbf{n}_{1}}{p}\biggr)\biggr|\ll |S|\frac{\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}_{1}};\end{eqnarray}$$
on the other hand, from (4.31) we have the identity
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}e\biggl(\unicode[STIX]{x1D719}(\mathbf{n}_{1}+h)-\frac{\unicode[STIX]{x1D709}(\mathbf{n}_{1}+h)}{p}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =e\biggl(\unicode[STIX]{x1D719}(h)-\frac{\unicode[STIX]{x1D709}h}{p}\biggr)\mathbb{E}e\biggl(\unicode[STIX]{x1D719}(\mathbf{n}_{1})-\frac{\unicode[STIX]{x1D709}\mathbf{n}_{1}}{p}+\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(\mathbf{n}_{1},h)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}e\biggl(\unicode[STIX]{x1D719}(\mathbf{n}_{1}+h)-\frac{\unicode[STIX]{x1D709}(\mathbf{n}_{1}+h)}{p}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =e\biggl(\unicode[STIX]{x1D719}(h)-\frac{\unicode[STIX]{x1D709}h}{p}\biggr)\mathbb{E}e\biggl(\unicode[STIX]{x1D719}(\mathbf{n}_{1})-\frac{\unicode[STIX]{x1D709}\mathbf{n}_{1}}{p}+\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}(\mathbf{n}_{1},h)\biggr).\nonumber\end{eqnarray}$$
Combining this with (4.32), (4.35), and (2.2), we conclude that
 $$\begin{eqnarray}\biggl\|\unicode[STIX]{x1D719}(h)-\frac{\unicode[STIX]{x1D709}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\asymp \biggl|e\biggl(\unicode[STIX]{x1D719}(h)-\frac{\unicode[STIX]{x1D709}h}{p}\biggr)-1\biggr|\ll |S|\frac{\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}_{1}}\end{eqnarray}$$
$$\begin{eqnarray}\biggl\|\unicode[STIX]{x1D719}(h)-\frac{\unicode[STIX]{x1D709}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\asymp \biggl|e\biggl(\unicode[STIX]{x1D719}(h)-\frac{\unicode[STIX]{x1D709}h}{p}\biggr)-1\biggr|\ll |S|\frac{\Vert h\Vert _{S^{\bot }}}{\unicode[STIX]{x1D70C}_{1}}\end{eqnarray}$$
for all
 $h\in B(S,\unicode[STIX]{x1D70C}_{1})$
. As the claim (4.33) is trivial for
$h\in B(S,\unicode[STIX]{x1D70C}_{1})$
. As the claim (4.33) is trivial for
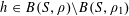 $h\in B(S,\unicode[STIX]{x1D70C})\backslash B(S,\unicode[STIX]{x1D70C}_{1})$
, the claim follows.◻
$h\in B(S,\unicode[STIX]{x1D70C})\backslash B(S,\unicode[STIX]{x1D70C}_{1})$
, the claim follows.◻
5 Dilated tori
As mentioned in Example 3 of §3, to maintain good quantitative control (and specifically, Lipschitz norm control) on the functions
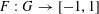 $F:G\rightarrow [-1,1]$
used to build quadratic approximants, one needs to generalize the underlying domain
$F:G\rightarrow [-1,1]$
used to build quadratic approximants, one needs to generalize the underlying domain
![]() $G$
to more general tori than the standard tori
$G$
to more general tori than the standard tori
![]() $(\mathbb{R}/\mathbb{Z})^{d}$
with the usual norm structure. It turns out that it will suffice to work with dilated tori of the form
$(\mathbb{R}/\mathbb{Z})^{d}$
with the usual norm structure. It turns out that it will suffice to work with dilated tori of the form
 $$\begin{eqnarray}G=\mathop{\prod }_{i=1}^{d}(\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}),\end{eqnarray}$$
$$\begin{eqnarray}G=\mathop{\prod }_{i=1}^{d}(\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}),\end{eqnarray}$$
where
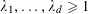 $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{d}\geqslant 1$
are real numbers. One can view this dilated torus as the quotient of
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{d}\geqslant 1$
are real numbers. One can view this dilated torus as the quotient of
![]() $\mathbb{R}^{d}$
by a dilated lattice
$\mathbb{R}^{d}$
by a dilated lattice
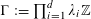 $\unicode[STIX]{x1D6E4}:=\prod _{i=1}^{d}\unicode[STIX]{x1D706}_{i}\mathbb{Z}$
. We can place a “norm” on
$\unicode[STIX]{x1D6E4}:=\prod _{i=1}^{d}\unicode[STIX]{x1D706}_{i}\mathbb{Z}$
. We can place a “norm” on
![]() $G$
by declaring
$G$
by declaring
![]() $\Vert x\Vert _{G}$
for
$\Vert x\Vert _{G}$
for
![]() $x\in G$
to be the Euclidean distance in
$x\in G$
to be the Euclidean distance in
![]() $\mathbb{R}^{d}$
from
$\mathbb{R}^{d}$
from
![]() $x$
to
$x$
to
![]() $\unicode[STIX]{x1D6E4}$
; this generalizes the norm
$\unicode[STIX]{x1D6E4}$
; this generalizes the norm
![]() $\Vert \Vert _{\mathbb{R}/\mathbb{Z}}$
from §2. This in turn defines a metric
$\Vert \Vert _{\mathbb{R}/\mathbb{Z}}$
from §2. This in turn defines a metric
![]() $d_{G}$
on
$d_{G}$
on
![]() $G$
by the formula
$G$
by the formula
 $$\begin{eqnarray}d_{G}(x,y):=\Vert x-y\Vert _{G}.\end{eqnarray}$$
$$\begin{eqnarray}d_{G}(x,y):=\Vert x-y\Vert _{G}.\end{eqnarray}$$
The volume
![]() $\operatorname{vol}(G)$
of a dilated torus is defined to be the product
$\operatorname{vol}(G)$
of a dilated torus is defined to be the product
 $$\begin{eqnarray}\operatorname{vol}(G):=\mathop{\prod }_{i=1}^{d}\unicode[STIX]{x1D706}_{i}=\det (\unicode[STIX]{x1D6E4}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}(G):=\mathop{\prod }_{i=1}^{d}\unicode[STIX]{x1D706}_{i}=\det (\unicode[STIX]{x1D6E4}).\end{eqnarray}$$
It will be important to keep this quantity under control during the iteration process. In particular, when transforming from one dilated torus to another, the volume of the new torus should behave like a linear function of the existing torus; anything worse than this (e.g. quadratic behaviour) will lead to undesirable bounds upon iteration.
We define the Pontryagin dual
![]() ${\hat{G}}$
of a dilated torus
${\hat{G}}$
of a dilated torus
![]() $G$
to be the lattice
$G$
to be the lattice
 $$\begin{eqnarray}{\hat{G}}:=\mathop{\prod }_{i=1}^{d}\frac{1}{\unicode[STIX]{x1D706}_{i}}\mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}{\hat{G}}:=\mathop{\prod }_{i=1}^{d}\frac{1}{\unicode[STIX]{x1D706}_{i}}\mathbb{Z}.\end{eqnarray}$$
Elements
![]() $k$
of this dual will be called dual frequencies of the torus. If
$k$
of this dual will be called dual frequencies of the torus. If
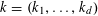 $k=(k_{1},\ldots ,k_{d})$
is a dual frequency and
$k=(k_{1},\ldots ,k_{d})$
is a dual frequency and
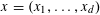 $x=(x_{1},\ldots ,x_{d})$
is an element of
$x=(x_{1},\ldots ,x_{d})$
is an element of
![]() $G$
, we define the dot product
$G$
, we define the dot product
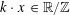 $k\cdot x\in \mathbb{R}/\mathbb{Z}$
in the usual fashion as
$k\cdot x\in \mathbb{R}/\mathbb{Z}$
in the usual fashion as
 $$\begin{eqnarray}k\cdot x=k_{1}x_{1}+\cdots +k_{d}x_{d}\end{eqnarray}$$
$$\begin{eqnarray}k\cdot x=k_{1}x_{1}+\cdots +k_{d}x_{d}\end{eqnarray}$$
noting that this gives a well-defined element of
![]() $\mathbb{R}/\mathbb{Z}$
.
$\mathbb{R}/\mathbb{Z}$
.
A dual frequency
![]() $k$
is said to be irreducible if it is non-zero, and not of the form
$k$
is said to be irreducible if it is non-zero, and not of the form
![]() $k=nk^{\prime }$
for some other dual frequency
$k=nk^{\prime }$
for some other dual frequency
![]() $k^{\prime }$
and some natural number
$k^{\prime }$
and some natural number
![]() $n>1$
. If a dual frequency
$n>1$
. If a dual frequency
![]() $k$
is irreducible, then its orthogonal complement
$k$
is irreducible, then its orthogonal complement
 $$\begin{eqnarray}k^{\bot }:=\{x\in G:k\cdot x=0\}\end{eqnarray}$$
$$\begin{eqnarray}k^{\bot }:=\{x\in G:k\cdot x=0\}\end{eqnarray}$$
is a
![]() $(d-1)$
-dimensional subtorus of
$(d-1)$
-dimensional subtorus of
![]() $G$
; it inherits a metric
$G$
; it inherits a metric
![]() $d_{k^{\bot }}$
from the torus
$d_{k^{\bot }}$
from the torus
![]() $G$
it lies in. We will need to pass to such a complement when dealing with poorly distributed quadratic factors (as in the third or fourth examples in §3), however we encounter the technical issue that these complements
$G$
it lies in. We will need to pass to such a complement when dealing with poorly distributed quadratic factors (as in the third or fourth examples in §3), however we encounter the technical issue that these complements
![]() $k^{\bot }$
will not quite be of the form of a dilated torus. However, we will be able to transform
$k^{\bot }$
will not quite be of the form of a dilated torus. However, we will be able to transform
![]() $k^{\bot }$
into a dilated torus using a bilipschitz transformation, as the following result shows.
$k^{\bot }$
into a dilated torus using a bilipschitz transformation, as the following result shows.
Theorem 5.1. Let
 $G=\prod _{i=1}^{d}(\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
be a dilated torus, and let
$G=\prod _{i=1}^{d}(\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
be a dilated torus, and let
![]() $k\in {\hat{G}}$
be an irreducible dual frequency of
$k\in {\hat{G}}$
be an irreducible dual frequency of
![]() $G$
. Then there exists a dilated torus
$G$
. Then there exists a dilated torus
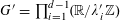 $G^{\prime }=\prod _{i=1}^{d-1}(\mathbb{R}/\unicode[STIX]{x1D706}_{i}^{\prime }\mathbb{Z})$
and a Lie group isomorphism
$G^{\prime }=\prod _{i=1}^{d-1}(\mathbb{R}/\unicode[STIX]{x1D706}_{i}^{\prime }\mathbb{Z})$
and a Lie group isomorphism
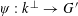 $\unicode[STIX]{x1D713}:k^{\bot }\rightarrow G^{\prime }$
obeying the bilipschitz bounds
$\unicode[STIX]{x1D713}:k^{\bot }\rightarrow G^{\prime }$
obeying the bilipschitz bounds
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}\Vert _{\operatorname{Lip}},\Vert \unicode[STIX]{x1D713}^{-1}\Vert _{\operatorname{ Lip}}\ll d^{O(d)}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}\Vert _{\operatorname{Lip}},\Vert \unicode[STIX]{x1D713}^{-1}\Vert _{\operatorname{ Lip}}\ll d^{O(d)}\end{eqnarray}$$
and such that one has the volume bound
 $$\begin{eqnarray}\operatorname{vol}(G^{\prime })=d^{O(d)}|k|\operatorname{vol}(G),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}(G^{\prime })=d^{O(d)}|k|\operatorname{vol}(G),\end{eqnarray}$$
where
![]() $|k|$
denotes the Euclidean magnitude of
$|k|$
denotes the Euclidean magnitude of
![]() $k$
in
$k$
in
![]() $\mathbb{R}^{d}$
.
$\mathbb{R}^{d}$
.
Proof. The case
![]() $d=0$
is vacuous and the case
$d=0$
is vacuous and the case
![]() $d=1$
is trivial, so we may assume
$d=1$
is trivial, so we may assume
![]() $d>1$
. One can identify
$d>1$
. One can identify
![]() $k^{\bot }$
with the quotient
$k^{\bot }$
with the quotient
![]() $V/\unicode[STIX]{x1D6E4}$
, where
$V/\unicode[STIX]{x1D6E4}$
, where
 $V:=\{x\in \mathbb{R}^{d}:k\cdot x=0\}$
is the hyperplane in
$V:=\{x\in \mathbb{R}^{d}:k\cdot x=0\}$
is the hyperplane in
![]() $\mathbb{R}^{d}$
orthogonal to
$\mathbb{R}^{d}$
orthogonal to
![]() $k$
(now viewed as an element of
$k$
(now viewed as an element of
![]() $\mathbb{R}^{d}$
), and
$\mathbb{R}^{d}$
), and
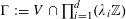 $\unicode[STIX]{x1D6E4}:=V\cap \prod _{i=1}^{d}(\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
is the restriction of the lattice
$\unicode[STIX]{x1D6E4}:=V\cap \prod _{i=1}^{d}(\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
is the restriction of the lattice
 $\prod _{i=1}^{d}(\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
to
$\prod _{i=1}^{d}(\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
to
![]() $V$
.
$V$
.
As
![]() $k$
is irreducible, there exists a vector
$k$
is irreducible, there exists a vector
![]() $e$
in the lattice
$e$
in the lattice
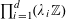 $\prod _{i=1}^{d}(\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
with
$\prod _{i=1}^{d}(\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
with
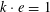 $k\cdot e=1$
; thus
$k\cdot e=1$
; thus
![]() $e$
has distance
$e$
has distance
![]() $1/|k|$
to
$1/|k|$
to
![]() $V$
. One can form a fundamental domain of
$V$
. One can form a fundamental domain of
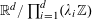 $\mathbb{R}^{d}/\prod _{i=1}^{d}(\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
by taking any fundamental domain for
$\mathbb{R}^{d}/\prod _{i=1}^{d}(\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
by taking any fundamental domain for
![]() $V/\unicode[STIX]{x1D6E4}$
and performing the Minkowski sum of that domain with the interval
$V/\unicode[STIX]{x1D6E4}$
and performing the Minkowski sum of that domain with the interval
 $\{te:0\leqslant t\leqslant 1\}$
. By Fubini’s theorem, the
$\{te:0\leqslant t\leqslant 1\}$
. By Fubini’s theorem, the
![]() $d$
-dimensional Lebesgue measure of such a sum will equal the
$d$
-dimensional Lebesgue measure of such a sum will equal the
![]() $(d-1)$
-dimensional Lebesgue measure of the fundamental domain of
$(d-1)$
-dimensional Lebesgue measure of the fundamental domain of
![]() $V/\unicode[STIX]{x1D6E4}$
and
$V/\unicode[STIX]{x1D6E4}$
and
![]() $1/|k|$
; thus the covolume of
$1/|k|$
; thus the covolume of
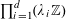 $\prod _{i=1}^{d}(\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
in
$\prod _{i=1}^{d}(\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
in
![]() $\mathbb{R}^{d}$
equals
$\mathbb{R}^{d}$
equals
![]() $1/|k|$
times the covolume of
$1/|k|$
times the covolume of
![]() $\unicode[STIX]{x1D6E4}$
in
$\unicode[STIX]{x1D6E4}$
in
![]() $V$
. As the former covolume (determinant) is
$V$
. As the former covolume (determinant) is
 $\prod _{i=1}^{d}\unicode[STIX]{x1D706}_{i}=\operatorname{vol}(G)$
, we conclude that
$\prod _{i=1}^{d}\unicode[STIX]{x1D706}_{i}=\operatorname{vol}(G)$
, we conclude that
![]() $\unicode[STIX]{x1D6E4}$
has covolume
$\unicode[STIX]{x1D6E4}$
has covolume
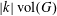 $|k|\operatorname{vol}(G)$
in
$|k|\operatorname{vol}(G)$
in
![]() $V$
.
$V$
.
Applying Lemma 4.8, we can find linearly independent elements
 $v_{1},\ldots ,v_{d-1}$
generating
$v_{1},\ldots ,v_{d-1}$
generating
![]() $\unicode[STIX]{x1D6E4}$
such that
$\unicode[STIX]{x1D6E4}$
such that
 $$\begin{eqnarray}B_{V}(0,O(d)^{-3d/2}t)\cap \unicode[STIX]{x1D6E4}\subset \biggl\{\mathop{\sum }_{i=1}^{r}n_{i}v_{i}:|n_{i}|\leqslant tN_{i}\biggr\}\subset B_{V}(0,t)\cap \unicode[STIX]{x1D6E4}\end{eqnarray}$$
$$\begin{eqnarray}B_{V}(0,O(d)^{-3d/2}t)\cap \unicode[STIX]{x1D6E4}\subset \biggl\{\mathop{\sum }_{i=1}^{r}n_{i}v_{i}:|n_{i}|\leqslant tN_{i}\biggr\}\subset B_{V}(0,t)\cap \unicode[STIX]{x1D6E4}\end{eqnarray}$$
for all
![]() $t>0$
, where
$t>0$
, where
 $B_{V}(0,r)$
is the Euclidean ball of radius
$B_{V}(0,r)$
is the Euclidean ball of radius
![]() $r$
in
$r$
in
![]() $V$
, and the
$V$
, and the
![]() $n_{i}$
are understood to be integers, with the bound
$n_{i}$
are understood to be integers, with the bound
 $$\begin{eqnarray}\mathop{\prod }_{i=1}^{d-1}N_{i}^{-1}=(2d)^{O(d)}|k|\operatorname{vol}(G).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{i=1}^{d-1}N_{i}^{-1}=(2d)^{O(d)}|k|\operatorname{vol}(G).\end{eqnarray}$$
From (5.3) we conclude in particular that
 $$\begin{eqnarray}O(d)^{-3d/2}N_{i}^{-1}\leqslant |v_{i}|\leqslant N_{i}^{-1}\end{eqnarray}$$
$$\begin{eqnarray}O(d)^{-3d/2}N_{i}^{-1}\leqslant |v_{i}|\leqslant N_{i}^{-1}\end{eqnarray}$$
for all
 $1\leqslant i\leqslant d$
.
$1\leqslant i\leqslant d$
.
We now define the
![]() $(d-1)$
-dimensional dilated torus
$(d-1)$
-dimensional dilated torus
 $$\begin{eqnarray}G^{\prime }:=\mathop{\prod }_{i=1}^{d-1}(\mathbb{R}/N_{i}^{-1}\mathbb{Z})\end{eqnarray}$$
$$\begin{eqnarray}G^{\prime }:=\mathop{\prod }_{i=1}^{d-1}(\mathbb{R}/N_{i}^{-1}\mathbb{Z})\end{eqnarray}$$
and the isomorphism
 $\unicode[STIX]{x1D719}:V/\unicode[STIX]{x1D6E4}\rightarrow G^{\prime }$
by the formula
$\unicode[STIX]{x1D719}:V/\unicode[STIX]{x1D6E4}\rightarrow G^{\prime }$
by the formula
 $$\begin{eqnarray}\unicode[STIX]{x1D719}\biggl(\mathop{\sum }_{i=1}^{d-1}t_{i}v_{i}~(\operatorname{mod}~\unicode[STIX]{x1D6E4})\biggr):=(t_{1}N_{1}^{-1},\ldots ,t_{d-1}N_{d-1}^{-1})\quad \biggl(\operatorname{mod}~\mathop{\prod }_{i=1}^{d-1}N_{i}^{-1}\mathbb{Z}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}\biggl(\mathop{\sum }_{i=1}^{d-1}t_{i}v_{i}~(\operatorname{mod}~\unicode[STIX]{x1D6E4})\biggr):=(t_{1}N_{1}^{-1},\ldots ,t_{d-1}N_{d-1}^{-1})\quad \biggl(\operatorname{mod}~\mathop{\prod }_{i=1}^{d-1}N_{i}^{-1}\mathbb{Z}\biggr)\end{eqnarray}$$
for real numbers
 $t_{1},\ldots ,t_{d-1}$
. It is easy to see that this is a Lie group isomorphism, and the bound (5.2) follows from (5.4). It remains to establish the bilipschitz bounds (5.1). It suffices to show that the linear isomorphism
$t_{1},\ldots ,t_{d-1}$
. It is easy to see that this is a Lie group isomorphism, and the bound (5.2) follows from (5.4). It remains to establish the bilipschitz bounds (5.1). It suffices to show that the linear isomorphism
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{d-1}t_{i}v_{i}\mapsto (t_{1}N_{1}^{-1},\ldots ,t_{d-1}N_{d-1}^{-1})\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{d-1}t_{i}v_{i}\mapsto (t_{1}N_{1}^{-1},\ldots ,t_{d-1}N_{d-1}^{-1})\end{eqnarray}$$
from
![]() $V$
to
$V$
to
![]() $\mathbb{R}^{d-1}$
, together with its inverse, have an operator norm of
$\mathbb{R}^{d-1}$
, together with its inverse, have an operator norm of
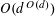 $O(d^{O(d)})$
. For the inverse map, this is clear from (5.5). For the forward map, it suffices from Cramer’s rule to show that
$O(d^{O(d)})$
. For the inverse map, this is clear from (5.5). For the forward map, it suffices from Cramer’s rule to show that
 $$\begin{eqnarray}\frac{|v_{1}\wedge \cdots \wedge v_{i-1}\wedge x\wedge v_{i+1}\wedge \cdots \wedge v_{d-1}|}{|v_{1}\wedge \cdots \wedge v_{d-1}|}\ll \frac{d^{O(d)}}{\unicode[STIX]{x1D706}_{i}^{\prime }}\end{eqnarray}$$
$$\begin{eqnarray}\frac{|v_{1}\wedge \cdots \wedge v_{i-1}\wedge x\wedge v_{i+1}\wedge \cdots \wedge v_{d-1}|}{|v_{1}\wedge \cdots \wedge v_{d-1}|}\ll \frac{d^{O(d)}}{\unicode[STIX]{x1D706}_{i}^{\prime }}\end{eqnarray}$$
for all
 $i=1,\ldots ,d-1$
and all unit vectors
$i=1,\ldots ,d-1$
and all unit vectors
![]() $x$
in
$x$
in
![]() $V$
. But from (5.5) the numerator is at most
$V$
. But from (5.5) the numerator is at most
 $\prod _{1\leqslant i^{\prime }\leqslant d-1:i^{\prime }\neq i}N_{i^{\prime }}^{-1}$
, while the denominator is the volume of a fundamental domain in
$\prod _{1\leqslant i^{\prime }\leqslant d-1:i^{\prime }\neq i}N_{i^{\prime }}^{-1}$
, while the denominator is the volume of a fundamental domain in
![]() $V$
and is thus equal to
$V$
and is thus equal to
 $d^{O(d)}N_{1}^{-1}\ldots N_{d-1}^{-1}$
thanks to (5.4). The claim follows.◻
$d^{O(d)}N_{1}^{-1}\ldots N_{d-1}^{-1}$
thanks to (5.4). The claim follows.◻
6 Constructing the approximants
In this section we construct the abstract directed graph
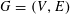 $G=(V,E)$
that appears in Proposition 3.3. For the rest of the paper, the prime
$G=(V,E)$
that appears in Proposition 3.3. For the rest of the paper, the prime
![]() $p$
, the function
$p$
, the function
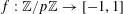 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
, and the parameter
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
, and the parameter
![]() $\unicode[STIX]{x1D702}$
with
$\unicode[STIX]{x1D702}$
with
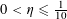 $0<\unicode[STIX]{x1D702}\leqslant {\textstyle \frac{1}{10}}$
are fixed, and we assume that (3.21) holds.
$0<\unicode[STIX]{x1D702}\leqslant {\textstyle \frac{1}{10}}$
are fixed, and we assume that (3.21) holds.
We begin with a description of the structured approximants
![]() $v\in V$
.
$v\in V$
.
Definition 6.1 (Structured local approximant).
A structured local approximant is a tuple
 $$\begin{eqnarray}v=(C,\mathbf{c},(n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}))_{c\in C},(G_{c})_{c\in C},(F_{c})_{c\in C},(\unicode[STIX]{x1D6EF}_{c})_{c\in C})\end{eqnarray}$$
$$\begin{eqnarray}v=(C,\mathbf{c},(n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}))_{c\in C},(G_{c})_{c\in C},(F_{c})_{c\in C},(\unicode[STIX]{x1D6EF}_{c})_{c\in C})\end{eqnarray}$$
consisting of the following objects:
-
∙ a finite non-empty set
 $C$
;
$C$
; -
∙ a random variable
 $\mathbf{c}$
, which we call the label variable, taking values in
$\mathbf{c}$
, which we call the label variable, taking values in
 $C$
;
$C$
; -
∙ a shifted Bohr set
 $n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})$
associated to each label
$n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})$
associated to each label
 $c\in C$
;
$c\in C$
; -
∙ a dilated torus
 $G_{c}$
associated to each label
$G_{c}$
associated to each label
 $c\in C$
;
$c\in C$
; -
∙ a
 $1$
-Lipschitz function
$1$
-Lipschitz function
 $F_{c}:G_{c}\rightarrow [-1,1]$
associated to each label
$F_{c}:G_{c}\rightarrow [-1,1]$
associated to each label
 $c\in \mathbb{C}$
; and
$c\in \mathbb{C}$
; and -
∙ a locally quadratic function
 $\unicode[STIX]{x1D6EF}_{c}:n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})\rightarrow G_{c}$
associated to each label
$\unicode[STIX]{x1D6EF}_{c}:n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})\rightarrow G_{c}$
associated to each label
 $c\in C$
.
$c\in C$
.
We denote the collection of all structured local approximants (up to isomorphismFootnote
3
) as
![]() $V$
. Given any structured local approximant
$V$
. Given any structured local approximant
![]() $v\in V$
, we define the random variables
$v\in V$
, we define the random variables
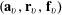 $(\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v})$
associated to
$(\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v})$
associated to
![]() $v$
by the following construction.
$v$
by the following construction.
-
(1) First, let
 $\mathbf{c}$
be the random label variable appearing above.
$\mathbf{c}$
be the random label variable appearing above. -
(2) For each
 $c\in C$
in the essential range of
$c\in C$
in the essential range of
 $\mathbf{c}$
, if we condition on the event
$\mathbf{c}$
, if we condition on the event
 $\mathbf{c}=c$
, we draw
$\mathbf{c}=c$
, we draw
 $\mathbf{a}_{v},\mathbf{r}_{v}$
independently and regularly from
$\mathbf{a}_{v},\mathbf{r}_{v}$
independently and regularly from
 $n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
and
$n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
and
 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively, and then we let
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively, and then we let
 $\mathbf{f}_{v}$
be the function
$\mathbf{f}_{v}$
be the function  $$\begin{eqnarray}\mathbf{f}_{v}(a):=F_{c}(\unicode[STIX]{x1D6EF}_{c}(a)).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{f}_{v}(a):=F_{c}(\unicode[STIX]{x1D6EF}_{c}(a)).\end{eqnarray}$$
Thus
![]() $\mathbf{f}_{v}$
is deterministic when
$\mathbf{f}_{v}$
is deterministic when
![]() $\mathbf{c}$
is conditioned to be fixed, but random when
$\mathbf{c}$
is conditioned to be fixed, but random when
![]() $\mathbf{c}$
is allowed to vary.
$\mathbf{c}$
is allowed to vary.
We also define the following additional statistics of the structured local approximant
![]() $v$
:
$v$
:
-
∙ the waste
 $\operatorname{waste}(v)$
is the quantity
$\operatorname{waste}(v)$
is the quantity
 $|\mathbb{E}f(\mathbf{a})-\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}f(a)|$
;
$|\mathbb{E}f(\mathbf{a})-\mathbb{E}_{a\in \mathbb{Z}/p\mathbb{Z}}f(a)|$
; -
∙ the
 $1$
-error
$1$
-error
 $\operatorname{Err}_{1}(v)$
is
$\operatorname{Err}_{1}(v)$
is
 $|\mathbb{E}\mathbf{f}(\mathbf{a})-\mathbb{E}f(\mathbf{a})|$
;
$|\mathbb{E}\mathbf{f}(\mathbf{a})-\mathbb{E}f(\mathbf{a})|$
; -
∙ the
 $4$
-error
$4$
-error
 $\operatorname{Err}_{4}(v)$
is
$\operatorname{Err}_{4}(v)$
is
 $|\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f})-\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f)|$
;
$|\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f})-\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f)|$
; -
∙ the energy
 $\operatorname{Energy}(v)$
is
$\operatorname{Energy}(v)$
is
 $\mathbb{E}|f(\mathbf{a})-\mathbf{f}(\mathbf{a})|^{2}$
;
$\mathbb{E}|f(\mathbf{a})-\mathbf{f}(\mathbf{a})|^{2}$
; -
∙ the linear rank
 $d_{1}(v)$
is
$d_{1}(v)$
is
 $\max _{c\in C}|S_{c}|$
;
$\max _{c\in C}|S_{c}|$
; -
∙ the quadratic dimension
 $d_{2}(v)$
is
$d_{2}(v)$
is
 $\max _{c\in C}\dim (G_{c})$
;
$\max _{c\in C}\dim (G_{c})$
; -
∙ the linear scale
 $\unicode[STIX]{x1D70C}(v)$
is
$\unicode[STIX]{x1D70C}(v)$
is
 $\min _{c\in C}\unicode[STIX]{x1D70C}_{c}$
;
$\min _{c\in C}\unicode[STIX]{x1D70C}_{c}$
; -
∙ the quadratic volume
 $\operatorname{vol}(v)$
is the quantity
$\operatorname{vol}(v)$
is the quantity
 $\max _{c\in C}\operatorname{vol}(G_{c})$
;
$\max _{c\in C}\operatorname{vol}(G_{c})$
; -
∙ the poorly distributed quadratic dimension
 $d_{2}^{\text{poor}}(v)$
is the maximum value of
$d_{2}^{\text{poor}}(v)$
is the maximum value of
 $\dim (G_{c})$
over all poorly distributed
$\dim (G_{c})$
over all poorly distributed
 $c$
in the essential range of
$c$
in the essential range of
 $\mathbf{c}$
, or zero if no such
$\mathbf{c}$
, or zero if no such
 $c$
exists. Here, an element
$c$
exists. Here, an element
 $c$
in the essential range of
$c$
in the essential range of
 $\mathbf{c}$
is said to be poorly distributed if one has (6.1)
$\mathbf{c}$
is said to be poorly distributed if one has (6.1) $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f|\mathbf{c}=c)<\mathbb{E}(\mathbf{f}(\mathbf{a})|\mathbf{c}=c)^{4}-\frac{\unicode[STIX]{x1D702}}{2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f|\mathbf{c}=c)<\mathbb{E}(\mathbf{f}(\mathbf{a})|\mathbf{c}=c)^{4}-\frac{\unicode[STIX]{x1D702}}{2}.\end{eqnarray}$$
This gives the set
![]() $V$
of structured local approximants for Proposition 3.3; we clearly have
$V$
of structured local approximants for Proposition 3.3; we clearly have
 $0\leqslant d_{2}^{\text{poor}}(v)\leqslant d_{2}(v)$
for all
$0\leqslant d_{2}^{\text{poor}}(v)\leqslant d_{2}(v)$
for all
![]() $v\in V$
.
$v\in V$
.
We now also define the initial approximant.
Definition 6.2. The initial approximant
![]() $v_{0}\in V$
is defined to be the tuple
$v_{0}\in V$
is defined to be the tuple
 $$\begin{eqnarray}v_{0}=(C,\mathbf{c},(n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}))_{c\in C},(G_{c})_{c\in C},(F_{c})_{c\in C},(\unicode[STIX]{x1D6EF}_{c})_{c\in C})\end{eqnarray}$$
$$\begin{eqnarray}v_{0}=(C,\mathbf{c},(n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}))_{c\in C},(G_{c})_{c\in C},(F_{c})_{c\in C},(\unicode[STIX]{x1D6EF}_{c})_{c\in C})\end{eqnarray}$$
defined as follows:
-
∙
 $C:=\mathbb{Z}/p\mathbb{Z}$
, and
$C:=\mathbb{Z}/p\mathbb{Z}$
, and
 $\mathbf{c}$
is drawn uniformly from
$\mathbf{c}$
is drawn uniformly from
 $C$
;
$C$
; -
∙ for each
 $c\in C$
, we have
$c\in C$
, we have
 $n_{c}:=0$
,
$n_{c}:=0$
,
 $S_{c}:=\{1\}$
, and
$S_{c}:=\{1\}$
, and
 $\unicode[STIX]{x1D70C}_{c}:=1$
;
$\unicode[STIX]{x1D70C}_{c}:=1$
; -
∙ for each
 $c\in C$
, the group
$c\in C$
, the group
 $G_{c}$
is the standard
$G_{c}$
is the standard
 $0$
-torus
$0$
-torus
 $(\mathbb{R}/\mathbb{Z})^{0}$
(that is to say, a point);
$(\mathbb{R}/\mathbb{Z})^{0}$
(that is to say, a point); -
∙ for each
 $c\in C$
, the function
$c\in C$
, the function
 $F_{c}:G_{c}\rightarrow [-1,1]$
is the zero function
$F_{c}:G_{c}\rightarrow [-1,1]$
is the zero function
 $F_{c}(x):=0$
;
$F_{c}(x):=0$
; -
∙ for each
 $c\in C$
, the function
$c\in C$
, the function
 $\unicode[STIX]{x1D6EF}_{c}:\mathbb{Z}/p\mathbb{Z}\rightarrow G_{c}$
is the unique (constant) map from
$\unicode[STIX]{x1D6EF}_{c}:\mathbb{Z}/p\mathbb{Z}\rightarrow G_{c}$
is the unique (constant) map from
 $\mathbb{Z}/p\mathbb{Z}$
to the point
$\mathbb{Z}/p\mathbb{Z}$
to the point
 $G_{c}$
.
$G_{c}$
.
By chasing the definitions, we see that
![]() $\mathbf{a}_{v_{0}}$
is uniformly distributed in
$\mathbf{a}_{v_{0}}$
is uniformly distributed in
![]() $\mathbb{Z}/p\mathbb{Z}$
, and we can compute several of the statistics of the initial approximant
$\mathbb{Z}/p\mathbb{Z}$
, and we can compute several of the statistics of the initial approximant
![]() $v_{0}$
:
$v_{0}$
:
 $$\begin{eqnarray}\operatorname{waste}(v_{0})=d_{2}^{\text{poor}}(v_{0})=d_{2}(v_{0})=0;d_{1}(v_{0})=\unicode[STIX]{x1D70C}(v)=\operatorname{vol}(v)=1.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{waste}(v_{0})=d_{2}^{\text{poor}}(v_{0})=d_{2}(v_{0})=0;d_{1}(v_{0})=\unicode[STIX]{x1D70C}(v)=\operatorname{vol}(v)=1.\end{eqnarray}$$
Now we define the edges of the graph
 $G(V,E)$
.
$G(V,E)$
.
Definition 6.3. We let
![]() $E$
be the set of all directed edges
$E$
be the set of all directed edges
![]() $v\rightarrow v^{\prime }$
, where
$v\rightarrow v^{\prime }$
, where
 $v,v^{\prime }\in V$
are structured local approximants such that
$v,v^{\prime }\in V$
are structured local approximants such that
 $$\begin{eqnarray}\displaystyle d_{1}(v^{\prime }) & {\leqslant} & \displaystyle d_{1}(v)+\unicode[STIX]{x1D702}^{-C_{2}},\nonumber\\ \displaystyle d_{2}(v^{\prime }) & {\leqslant} & \displaystyle d_{2}(v)+1,\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}(v^{\prime }) & {\geqslant} & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-C_{5}})\unicode[STIX]{x1D70C}(v),\nonumber\\ \displaystyle \operatorname{vol}(v^{\prime }) & {\leqslant} & \displaystyle \exp (\unicode[STIX]{x1D702}^{-C_{3}})\operatorname{vol}(v),\nonumber\\ \displaystyle |\text{waste}(v)-\operatorname{waste}(v^{\prime })| & {\leqslant} & \displaystyle \unicode[STIX]{x1D702}^{C_{3}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{1}(v^{\prime }) & {\leqslant} & \displaystyle d_{1}(v)+\unicode[STIX]{x1D702}^{-C_{2}},\nonumber\\ \displaystyle d_{2}(v^{\prime }) & {\leqslant} & \displaystyle d_{2}(v)+1,\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}(v^{\prime }) & {\geqslant} & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-C_{5}})\unicode[STIX]{x1D70C}(v),\nonumber\\ \displaystyle \operatorname{vol}(v^{\prime }) & {\leqslant} & \displaystyle \exp (\unicode[STIX]{x1D702}^{-C_{3}})\operatorname{vol}(v),\nonumber\\ \displaystyle |\text{waste}(v)-\operatorname{waste}(v^{\prime })| & {\leqslant} & \displaystyle \unicode[STIX]{x1D702}^{C_{3}}.\nonumber\end{eqnarray}$$
From this definition and (6.2) we have the following bounds on the various statistics of vertices of
![]() $V$
that are not too far from the initial vertex
$V$
that are not too far from the initial vertex
![]() $v_{0}$
, assuming that each constant
$v_{0}$
, assuming that each constant
![]() $C_{i}$
is chosen sufficiently large depending on the preceding constants
$C_{i}$
is chosen sufficiently large depending on the preceding constants
 $C_{1},\ldots ,C_{i-1}$
.
$C_{1},\ldots ,C_{i-1}$
.
Lemma 6.4. Suppose a vertex
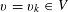 $v=v_{k}\in V$
can be reached from
$v=v_{k}\in V$
can be reached from
![]() $v_{0}$
by a path
$v_{0}$
by a path
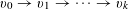 $v_{0}\rightarrow v_{1}\rightarrow \cdots \rightarrow v_{k}$
with
$v_{0}\rightarrow v_{1}\rightarrow \cdots \rightarrow v_{k}$
with
 $0\leqslant k\leqslant 8\unicode[STIX]{x1D702}^{-2C_{2}}$
. Then we have
$0\leqslant k\leqslant 8\unicode[STIX]{x1D702}^{-2C_{2}}$
. Then we have
 $$\begin{eqnarray}\displaystyle d_{1}(v) & {\leqslant} & \displaystyle 8\unicode[STIX]{x1D702}^{-3C_{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{1}(v) & {\leqslant} & \displaystyle 8\unicode[STIX]{x1D702}^{-3C_{2}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle d_{2}(v) & {\leqslant} & \displaystyle 8\unicode[STIX]{x1D702}^{-2C_{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{2}(v) & {\leqslant} & \displaystyle 8\unicode[STIX]{x1D702}^{-2C_{2}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}(v) & {\geqslant} & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-2C_{5}}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}(v) & {\geqslant} & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-2C_{5}}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \operatorname{vol}(v) & {\leqslant} & \displaystyle \exp (\unicode[STIX]{x1D702}^{-2C_{3}}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{vol}(v) & {\leqslant} & \displaystyle \exp (\unicode[STIX]{x1D702}^{-2C_{3}}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \operatorname{waste}(v) & {\leqslant} & \displaystyle \unicode[STIX]{x1D702}^{C_{3}/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{waste}(v) & {\leqslant} & \displaystyle \unicode[STIX]{x1D702}^{C_{3}/2}.\end{eqnarray}$$
From (6.7) we see in particular that the almost uniformity axiom in Proposition 3.3(ii) is obeyed. The thickness axiom in Proposition 3.3(i) is also easy, as the following corollary shows.
Corollary 6.5. Suppose a quadratic approximant
 $v=v_{k}\in V$
can be reached from
$v=v_{k}\in V$
can be reached from
![]() $v_{0}$
by a path
$v_{0}$
by a path
 $v_{0}\rightarrow v_{1}\rightarrow \cdots \rightarrow v_{k}$
of length
$v_{0}\rightarrow v_{1}\rightarrow \cdots \rightarrow v_{k}$
of length
![]() $k$
at most
$k$
at most
![]() $8\unicode[STIX]{x1D702}^{-2C_{2}}$
. Then we have
$8\unicode[STIX]{x1D702}^{-2C_{2}}$
. Then we have
 $\mathbb{P}(\mathbf{r}_{v}=0)\ll \exp (\unicode[STIX]{x1D702}^{-C_{5}^{2}})/p$
.
$\mathbb{P}(\mathbf{r}_{v}=0)\ll \exp (\unicode[STIX]{x1D702}^{-C_{5}^{2}})/p$
.
Proof. Write
 $$\begin{eqnarray}v=(C,\mathbf{c},(n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}))_{c\in C},(G_{c})_{c\in C},(F_{c})_{c\in C},(\unicode[STIX]{x1D6EF}_{c})_{c\in C}).\end{eqnarray}$$
$$\begin{eqnarray}v=(C,\mathbf{c},(n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}))_{c\in C},(G_{c})_{c\in C},(F_{c})_{c\in C},(\unicode[STIX]{x1D6EF}_{c})_{c\in C}).\end{eqnarray}$$
It suffices to show that
 $$\begin{eqnarray}\mathbb{P}(\mathbf{r}_{v}=0|\mathbf{c}=c)\ll \exp (\unicode[STIX]{x1D702}^{-C_{5}^{2}})/p\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{r}_{v}=0|\mathbf{c}=c)\ll \exp (\unicode[STIX]{x1D702}^{-C_{5}^{2}})/p\end{eqnarray}$$
for each
![]() $c$
in the essential range of
$c$
in the essential range of
![]() $\mathbf{c}$
. But once
$\mathbf{c}$
. But once
![]() $\mathbf{c}$
is fixed to equal
$\mathbf{c}$
is fixed to equal
![]() $\mathbf{c}$
, then
$\mathbf{c}$
, then
![]() $\mathbf{r}_{v}$
is drawn regularly from
$\mathbf{r}_{v}$
is drawn regularly from
 $n_{c}+B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C}_{c})$
. By Lemma 6.4,
$n_{c}+B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C}_{c})$
. By Lemma 6.4,
![]() $S_{c}$
has cardinality at most
$S_{c}$
has cardinality at most
![]() $8\unicode[STIX]{x1D702}^{-3C_{2}}$
and
$8\unicode[STIX]{x1D702}^{-3C_{2}}$
and
![]() $\unicode[STIX]{x1D70C}_{c}$
is at least
$\unicode[STIX]{x1D70C}_{c}$
is at least
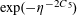 $\exp (-\unicode[STIX]{x1D702}^{-2C_{5}})$
. The claim now follows from Lemma 4.2.◻
$\exp (-\unicode[STIX]{x1D702}^{-2C_{5}})$
. The claim now follows from Lemma 4.2.◻
It remains to verify the last two axioms (iii), (iv) of Proposition 3.3. We isolate these statements formally, using Lemma 6.4 and Definition 6.3.
The first of these results, Theorem 6.6, states that “a bad approximation implies an energy decrement”. The second, Theorem 6.7, states that “a bad lower bound implies a dimension increment”.
Theorem 6.6. Let the notation and hypotheses be as above. Suppose that
![]() $v\in V$
is a structured local approximant obeying (6.3)–(6.6). If we have
$v\in V$
is a structured local approximant obeying (6.3)–(6.6). If we have
 $$\begin{eqnarray}\operatorname{Err}_{1}(v)>\unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Err}_{1}(v)>\unicode[STIX]{x1D702}\end{eqnarray}$$
or
 $$\begin{eqnarray}\operatorname{Err}_{4}(v)>\unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Err}_{4}(v)>\unicode[STIX]{x1D702}\end{eqnarray}$$
then there exists a structured local approximant
![]() $v^{\prime }$
obeying the bounds
$v^{\prime }$
obeying the bounds
 $$\begin{eqnarray}\displaystyle d(v^{\prime }) & {\leqslant} & \displaystyle d(v)+\unicode[STIX]{x1D702}^{-C_{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d(v^{\prime }) & {\leqslant} & \displaystyle d(v)+\unicode[STIX]{x1D702}^{-C_{2}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle d_{2}(v^{\prime }) & {\leqslant} & \displaystyle d_{2}(v)+1,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{2}(v^{\prime }) & {\leqslant} & \displaystyle d_{2}(v)+1,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}(v^{\prime }) & {\geqslant} & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-C_{5}})\unicode[STIX]{x1D70C}(v),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}(v^{\prime }) & {\geqslant} & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-C_{5}})\unicode[STIX]{x1D70C}(v),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \operatorname{vol}(v^{\prime }) & {\leqslant} & \displaystyle \exp (\unicode[STIX]{x1D702}^{-C_{3}})\operatorname{vol}(v),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{vol}(v^{\prime }) & {\leqslant} & \displaystyle \exp (\unicode[STIX]{x1D702}^{-C_{3}})\operatorname{vol}(v),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle |\text{waste}(v^{\prime })-\operatorname{waste}(v)| & {\leqslant} & \displaystyle \unicode[STIX]{x1D702}^{C_{3}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\text{waste}(v^{\prime })-\operatorname{waste}(v)| & {\leqslant} & \displaystyle \unicode[STIX]{x1D702}^{C_{3}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \operatorname{Energy}(v^{\prime }) & {\leqslant} & \displaystyle \operatorname{Energy}(v)-\unicode[STIX]{x1D702}^{C_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Energy}(v^{\prime }) & {\leqslant} & \displaystyle \operatorname{Energy}(v)-\unicode[STIX]{x1D702}^{C_{2}}.\end{eqnarray}$$
Theorem 6.7. Let the notation and hypotheses be as above. Suppose that
![]() $v\in V$
is a structured local approximant obeying (6.3)–(6.6), and let
$v\in V$
is a structured local approximant obeying (6.3)–(6.6), and let
 $\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v}$
be the random variables associated to
$\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v}$
be the random variables associated to
![]() $v$
. If we have
$v$
. If we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v},\mathbf{r}_{v}}(\mathbf{f}_{v})\leqslant (\mathbb{E}\mathbf{f}_{v}(\mathbf{a}_{v}))^{4}-\unicode[STIX]{x1D702},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a}_{v},\mathbf{r}_{v}}(\mathbf{f}_{v})\leqslant (\mathbb{E}\mathbf{f}_{v}(\mathbf{a}_{v}))^{4}-\unicode[STIX]{x1D702},\end{eqnarray}$$
then there exists a quadratic approximant
![]() $v^{\prime }\in V$
with
$v^{\prime }\in V$
with
 $$\begin{eqnarray}\displaystyle d(v^{\prime }) & {\leqslant} & \displaystyle d(v)+\unicode[STIX]{x1D702}^{-C_{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d(v^{\prime }) & {\leqslant} & \displaystyle d(v)+\unicode[STIX]{x1D702}^{-C_{2}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle d_{2}(v^{\prime }) & {\leqslant} & \displaystyle d_{2}(v),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{2}(v^{\prime }) & {\leqslant} & \displaystyle d_{2}(v),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle d_{2}^{\text{poor}}(v^{\prime }) & {\leqslant} & \displaystyle d_{2}^{\text{poor}}(v)-1,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{2}^{\text{poor}}(v^{\prime }) & {\leqslant} & \displaystyle d_{2}^{\text{poor}}(v)-1,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}(v^{\prime }) & {\geqslant} & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-C_{5}})\unicode[STIX]{x1D70C}(v),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}(v^{\prime }) & {\geqslant} & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-C_{5}})\unicode[STIX]{x1D70C}(v),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \operatorname{vol}(v^{\prime }) & {\leqslant} & \displaystyle \exp (\unicode[STIX]{x1D702}^{-C_{3}})\operatorname{vol}(v),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{vol}(v^{\prime }) & {\leqslant} & \displaystyle \exp (\unicode[STIX]{x1D702}^{-C_{3}})\operatorname{vol}(v),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle |\text{waste}(v^{\prime })-\operatorname{waste}(v)| & {\leqslant} & \displaystyle \unicode[STIX]{x1D702}^{C_{3}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\text{waste}(v^{\prime })-\operatorname{waste}(v)| & {\leqslant} & \displaystyle \unicode[STIX]{x1D702}^{C_{3}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \operatorname{Energy}(v^{\prime }) & {\leqslant} & \displaystyle \operatorname{Energy}(v)+\unicode[STIX]{x1D702}^{3C_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Energy}(v^{\prime }) & {\leqslant} & \displaystyle \operatorname{Energy}(v)+\unicode[STIX]{x1D702}^{3C_{2}}.\end{eqnarray}$$
It remains to prove Theorems 6.6 and 6.7. Theorem 6.6 will be proven in §8 using a difficult local inverse Gowers theorem, Theorem 8.1, that will be proven in later sections. Theorem 6.7, on the other hand, will not rely on the local inverse Gowers theorem; it is proven in §7.
7 Bad lower bound implies dimension decrement
In this section we prove Theorem 6.7. Let the notation and hypotheses be as in Theorem 6.7. We abbreviate
 $\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v}$
as
$\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v}$
as
![]() $\mathbf{a},\mathbf{r},\mathbf{f}$
respectively. We can write the left-hand side of (6.16) as
$\mathbf{a},\mathbf{r},\mathbf{f}$
respectively. We can write the left-hand side of (6.16) as
![]() $\mathbb{E}A(\mathbf{c})$
, where for any
$\mathbb{E}A(\mathbf{c})$
, where for any
![]() $c\in C$
, the quantity
$c\in C$
, the quantity
![]() $A(c)$
is defined as the conditional expectation
$A(c)$
is defined as the conditional expectation
 $$\begin{eqnarray}A(c):=\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}|\mathbf{c}=c).\end{eqnarray}$$
$$\begin{eqnarray}A(c):=\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}|\mathbf{c}=c).\end{eqnarray}$$
Similarly, we can write
 $\mathbb{E}\mathbf{f}(\mathbf{a})=\mathbb{E}B(\mathbf{c})$
, where
$\mathbb{E}\mathbf{f}(\mathbf{a})=\mathbb{E}B(\mathbf{c})$
, where
 $B(\mathbf{c}):=\mathbb{E}(\mathbf{f}(\mathbf{a})|\mathbf{c}=c)$
. By (6.16) and Hölder’s inequality, we thus have
$B(\mathbf{c}):=\mathbb{E}(\mathbf{f}(\mathbf{a})|\mathbf{c}=c)$
. By (6.16) and Hölder’s inequality, we thus have
 $$\begin{eqnarray}\mathbb{E}B(\mathbf{c})^{4}-A(\mathbf{c})\geqslant \unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}B(\mathbf{c})^{4}-A(\mathbf{c})\geqslant \unicode[STIX]{x1D702}.\end{eqnarray}$$
Applying Lemma 2.2, we must therefore have
 $$\begin{eqnarray}\mathbb{P}(B(\mathbf{c})^{4}-A(\mathbf{c})>\unicode[STIX]{x1D702}/2)\gg \unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(B(\mathbf{c})^{4}-A(\mathbf{c})>\unicode[STIX]{x1D702}/2)\gg \unicode[STIX]{x1D702}.\end{eqnarray}$$
By (6.1), we conclude that
![]() $\mathbf{c}$
is poorly distributed with probability
$\mathbf{c}$
is poorly distributed with probability
![]() $\gg \unicode[STIX]{x1D702}$
. In particular, there is at least one poorly distributed value of
$\gg \unicode[STIX]{x1D702}$
. In particular, there is at least one poorly distributed value of
![]() $c$
.
$c$
.
Most of this section will be devoted to the proof of the following proposition, which roughly speaking asserts that when
![]() $\mathbf{c}$
is poorly distributed, there is a linear constraint between the quadratic frequencies that will ultimately allow us to decrease the poorly distributed quadratic dimension
$\mathbf{c}$
is poorly distributed, there is a linear constraint between the quadratic frequencies that will ultimately allow us to decrease the poorly distributed quadratic dimension
![]() $d_{2}^{\text{poor}}$
.
$d_{2}^{\text{poor}}$
.
Proposition 7.1. Let
![]() $c$
be a poorly distributed element of the essential range of
$c$
be a poorly distributed element of the essential range of
![]() $\mathbf{c}$
. Then there exists a natural number
$\mathbf{c}$
. Then there exists a natural number
![]() $m_{c}$
, a frequency
$m_{c}$
, a frequency
 $\unicode[STIX]{x1D709}_{c}\in \mathbb{Z}/p\mathbb{Z}$
and an irreducible dual frequency
$\unicode[STIX]{x1D709}_{c}\in \mathbb{Z}/p\mathbb{Z}$
and an irreducible dual frequency
![]() $k_{c}^{\prime }\in {\hat{G}}_{c}$
with
$k_{c}^{\prime }\in {\hat{G}}_{c}$
with
 $$\begin{eqnarray}1\leqslant m_{c}\ll \exp (\unicode[STIX]{x1D702}^{-4C_{3}})\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant m_{c}\ll \exp (\unicode[STIX]{x1D702}^{-4C_{3}})\end{eqnarray}$$
and
 $$\begin{eqnarray}\exp (-\unicode[STIX]{x1D702}^{-4C_{3}})\ll |k_{c}^{\prime }|\ll \exp (\unicode[STIX]{x1D702}^{-3C_{2}})\end{eqnarray}$$
$$\begin{eqnarray}\exp (-\unicode[STIX]{x1D702}^{-4C_{3}})\ll |k_{c}^{\prime }|\ll \exp (\unicode[STIX]{x1D702}^{-3C_{2}})\end{eqnarray}$$
such that
 $$\begin{eqnarray}\Vert k_{c}^{\prime }\cdot \unicode[STIX]{x1D6EF}_{c}(a+2m_{c}h)-k_{c}^{\prime }\cdot \unicode[STIX]{x1D6EF}_{c}(a)\!\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-3C_{4}})\end{eqnarray}$$
$$\begin{eqnarray}\Vert k_{c}^{\prime }\cdot \unicode[STIX]{x1D6EF}_{c}(a+2m_{c}h)-k_{c}^{\prime }\cdot \unicode[STIX]{x1D6EF}_{c}(a)\!\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-3C_{4}})\end{eqnarray}$$
for all
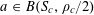 $a\in B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
and
$a\in B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
and
 $h\in B(S_{c}\cup \{\unicode[STIX]{x1D709}_{c}\},\exp (-\unicode[STIX]{x1D702}^{-5C_{4}})\unicode[STIX]{x1D70C})$
.
$h\in B(S_{c}\cup \{\unicode[STIX]{x1D709}_{c}\},\exp (-\unicode[STIX]{x1D702}^{-5C_{4}})\unicode[STIX]{x1D70C})$
.
A key technical point here is that the upper bound on
![]() $|k_{c}^{\prime }|$
involves only
$|k_{c}^{\prime }|$
involves only
![]() $C_{2}$
and not
$C_{2}$
and not
![]() $C_{3}$
or
$C_{3}$
or
![]() $C_{4}$
; this is necessary to keep the bounds under control during the iteration process. However, we will be able to tolerate the presence of the
$C_{4}$
; this is necessary to keep the bounds under control during the iteration process. However, we will be able to tolerate the presence of the
![]() $C_{3}$
and
$C_{3}$
and
![]() $C_{4}$
constants in the other components of Proposition 7.1.
$C_{4}$
constants in the other components of Proposition 7.1.
Proof. We condition on the event
![]() $\mathbf{c}=c$
. By Definition 6.1, the random variables
$\mathbf{c}=c$
. By Definition 6.1, the random variables
![]() $\mathbf{a},\mathbf{r}$
are now independent and regularly drawn from
$\mathbf{a},\mathbf{r}$
are now independent and regularly drawn from
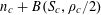 $n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
and
$n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
and
 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively, while
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively, while
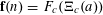 $\mathbf{f}(n)=F_{c}(\unicode[STIX]{x1D6EF}_{c}(a))$
. We conclude that
$\mathbf{f}(n)=F_{c}(\unicode[STIX]{x1D6EF}_{c}(a))$
. We conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}(F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}))F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r}))F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r}))F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+3\mathbf{r}))|\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad <\mathbb{E}(F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}))|\mathbf{c}=c)^{4}-\unicode[STIX]{x1D702}/2.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}(F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}))F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r}))F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r}))F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+3\mathbf{r}))|\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad <\mathbb{E}(F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}))|\mathbf{c}=c)^{4}-\unicode[STIX]{x1D702}/2.\nonumber\end{eqnarray}$$
Since
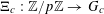 $\unicode[STIX]{x1D6EF}_{c}:\mathbb{Z}/p\mathbb{Z}\rightarrow G_{c}$
is locally quadratic on
$\unicode[STIX]{x1D6EF}_{c}:\mathbb{Z}/p\mathbb{Z}\rightarrow G_{c}$
is locally quadratic on
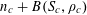 $n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})$
, which contains the progression
$n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})$
, which contains the progression
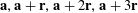 $\mathbf{a},\mathbf{a}+\mathbf{r},\mathbf{a}+2\mathbf{r},\mathbf{a}+3\mathbf{r}$
, we see from (4.17) that
$\mathbf{a},\mathbf{a}+\mathbf{r},\mathbf{a}+2\mathbf{r},\mathbf{a}+3\mathbf{r}$
, we see from (4.17) that
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{c}(\mathbf{a})-3\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r})+3\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r})-\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+3\mathbf{r})=0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{c}(\mathbf{a})-3\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r})+3\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r})-\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+3\mathbf{r})=0\end{eqnarray}$$
and so the left-hand side can be written as
 $$\begin{eqnarray}\mathbb{E}(F_{c}^{(3)}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r}))|\mathbf{c}=c),\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}(F_{c}^{(3)}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r}))|\mathbf{c}=c),\end{eqnarray}$$
where
 $F_{c}^{(3)}:G_{c}^{3}\rightarrow [-1,1]$
is the function
$F_{c}^{(3)}:G_{c}^{3}\rightarrow [-1,1]$
is the function
 $$\begin{eqnarray}F_{c}^{(3)}(x_{0},x_{1},x_{2}):=F_{c}(x_{0})F_{c}(x_{1})F_{c}(x_{2})F_{c}(x_{0}-3x_{1}+3x_{2}).\end{eqnarray}$$
$$\begin{eqnarray}F_{c}^{(3)}(x_{0},x_{1},x_{2}):=F_{c}(x_{0})F_{c}(x_{1})F_{c}(x_{2})F_{c}(x_{0}-3x_{1}+3x_{2}).\end{eqnarray}$$
Applying Lemma 3.2, we have
 $$\begin{eqnarray}\int _{G_{c}^{3}}F_{c}^{(3)}(x_{0},x_{1},x_{2})\,d\unicode[STIX]{x1D707}_{c}(x_{0})\,d\unicode[STIX]{x1D707}_{c}(x_{1})\,d\unicode[STIX]{x1D707}_{c}(x_{2})\geqslant \biggl(\int _{G_{c}}F_{c}(x)\,d\unicode[STIX]{x1D707}_{c}(x)\biggr)^{4},\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{c}^{3}}F_{c}^{(3)}(x_{0},x_{1},x_{2})\,d\unicode[STIX]{x1D707}_{c}(x_{0})\,d\unicode[STIX]{x1D707}_{c}(x_{1})\,d\unicode[STIX]{x1D707}_{c}(x_{2})\geqslant \biggl(\int _{G_{c}}F_{c}(x)\,d\unicode[STIX]{x1D707}_{c}(x)\biggr)^{4},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D707}_{c}$
is the probability Haar measure on
$\unicode[STIX]{x1D707}_{c}$
is the probability Haar measure on
![]() $G_{c}$
. By the triangle inequality, we conclude that at least one of the assertions
$G_{c}$
. By the triangle inequality, we conclude that at least one of the assertions
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathbb{E}(F_{c}^{(3)}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r}))|\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\int _{G_{c}^{3}}F_{c}^{(3)}(x_{0},x_{1},x_{2})\,d\unicode[STIX]{x1D707}_{c}(x_{0})\,d\unicode[STIX]{x1D707}_{c}(x_{1})\,d\unicode[STIX]{x1D707}_{c}(x_{2})\biggr|\gg \unicode[STIX]{x1D702}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\mathbb{E}(F_{c}^{(3)}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r}))|\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\int _{G_{c}^{3}}F_{c}^{(3)}(x_{0},x_{1},x_{2})\,d\unicode[STIX]{x1D707}_{c}(x_{0})\,d\unicode[STIX]{x1D707}_{c}(x_{1})\,d\unicode[STIX]{x1D707}_{c}(x_{2})\biggr|\gg \unicode[STIX]{x1D702}\nonumber\end{eqnarray}$$
or
 $$\begin{eqnarray}\biggl|\mathbb{E}(F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}))|\mathbf{c}=c)-\int _{G_{c}}F_{c}(x)\,d\unicode[STIX]{x1D707}_{c}(x)\biggr|\gg \unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathbb{E}(F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}))|\mathbf{c}=c)-\int _{G_{c}}F_{c}(x)\,d\unicode[STIX]{x1D707}_{c}(x)\biggr|\gg \unicode[STIX]{x1D702}\end{eqnarray}$$
holds. Defining
 $\tilde{F}:G_{c}^{3}\rightarrow [-1,1]$
by
$\tilde{F}:G_{c}^{3}\rightarrow [-1,1]$
by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \tilde{F}(x_{0},x_{1},x_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{10}\biggl(F_{c}^{(3)}(x_{0},x_{1},x_{2})-\int _{G_{c}^{3}}F_{c}^{(3)}(x_{0},x_{1},x_{2})\,d\unicode[STIX]{x1D707}_{c}(x_{0})\,d\unicode[STIX]{x1D707}_{c}(x_{1})\,d\unicode[STIX]{x1D707}_{c}(x_{2})\biggr)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \tilde{F}(x_{0},x_{1},x_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{10}\biggl(F_{c}^{(3)}(x_{0},x_{1},x_{2})-\int _{G_{c}^{3}}F_{c}^{(3)}(x_{0},x_{1},x_{2})\,d\unicode[STIX]{x1D707}_{c}(x_{0})\,d\unicode[STIX]{x1D707}_{c}(x_{1})\,d\unicode[STIX]{x1D707}_{c}(x_{2})\biggr)\nonumber\end{eqnarray}$$
in the former case and
 $$\begin{eqnarray}\tilde{F}(x_{0},x_{1},x_{2}):=\frac{1}{10}\biggl(F_{c}(x_{0})-\int _{G_{c}}F_{c}(x_{0})\,d\unicode[STIX]{x1D707}_{c}(x_{0})\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\tilde{F}(x_{0},x_{1},x_{2}):=\frac{1}{10}\biggl(F_{c}(x_{0})-\int _{G_{c}}F_{c}(x_{0})\,d\unicode[STIX]{x1D707}_{c}(x_{0})\biggr)\end{eqnarray}$$
in the latter case, we see that
![]() $\tilde{F}$
is
$\tilde{F}$
is
![]() $1$
-Lipschitz and of mean zero, and
$1$
-Lipschitz and of mean zero, and
 $$\begin{eqnarray}|\mathbb{E}(\tilde{F}(\mathbf{x}_{c})|\mathbf{c}=c)|\gg \unicode[STIX]{x1D702},\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(\tilde{F}(\mathbf{x}_{c})|\mathbf{c}=c)|\gg \unicode[STIX]{x1D702},\end{eqnarray}$$
where
![]() $\mathbf{x}_{c}\in G_{c}^{3}$
is the random variable
$\mathbf{x}_{c}\in G_{c}^{3}$
is the random variable
 $$\begin{eqnarray}\mathbf{x}_{c}:=(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r})).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{x}_{c}:=(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r}),\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r})).\end{eqnarray}$$
The Weyl equidistribution criterion, applied in the contrapositive, then suggests that there should be a non-zero dual frequency
 $k=(k_{1},k_{2},k_{3})\in {\hat{G}}_{c}^{3}$
to
$k=(k_{1},k_{2},k_{3})\in {\hat{G}}_{c}^{3}$
to
![]() $G_{c}^{3}$
such that
$G_{c}^{3}$
such that
 $\mathbb{E}(e(k\cdot \mathbf{x}_{c})|\mathbf{c}=c)$
is large. The next lemma makes this intuition precise.
$\mathbb{E}(e(k\cdot \mathbf{x}_{c})|\mathbf{c}=c)$
is large. The next lemma makes this intuition precise.
Lemma 7.2 (Weyl equidistribution).
With the notation and hypotheses as above, there exists a non-zero dual frequency
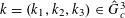 $k=(k_{1},k_{2},k_{3})\in {\hat{G}}_{c}^{3}$
to
$k=(k_{1},k_{2},k_{3})\in {\hat{G}}_{c}^{3}$
to
![]() $G_{c}^{3}$
with
$G_{c}^{3}$
with
 $|k|\ll \exp (O(\unicode[STIX]{x1D702}^{-3C_{2}}))$
such that
$|k|\ll \exp (O(\unicode[STIX]{x1D702}^{-3C_{2}}))$
such that
 $$\begin{eqnarray}|\mathbb{E}(k\cdot \mathbf{x}_{c}|\mathbf{c}=c)|\gg \exp (-O(\unicode[STIX]{x1D702}^{-3C_{2}}))/\text{vol}(G_{c}).\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(k\cdot \mathbf{x}_{c}|\mathbf{c}=c)|\gg \exp (-O(\unicode[STIX]{x1D702}^{-3C_{2}}))/\text{vol}(G_{c}).\end{eqnarray}$$
A key point here is that the bound on
![]() $|k|$
does not depend on the volume of the dilated torus
$|k|$
does not depend on the volume of the dilated torus
![]() $G_{c}$
, which will typically be much larger than
$G_{c}$
, which will typically be much larger than
 $\unicode[STIX]{x1D702}^{-2C_{2}-10}$
.
$\unicode[STIX]{x1D702}^{-2C_{2}-10}$
.
Proof. Write
 $G_{c}=\prod _{i=1}^{d}(\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
, thus
$G_{c}=\prod _{i=1}^{d}(\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
, thus
 $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{d}\geqslant 1$
, and by (6.4) one has
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{d}\geqslant 1$
, and by (6.4) one has
 $$\begin{eqnarray}d\leqslant 8\unicode[STIX]{x1D702}^{-2C_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}d\leqslant 8\unicode[STIX]{x1D702}^{-2C_{2}}.\end{eqnarray}$$
The bound (7.4) is not possible when
![]() $d=0$
, so we may assume
$d=0$
, so we may assume
![]() $d\geqslant 1$
. We can write
$d\geqslant 1$
. We can write
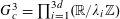 $G_{c}^{3}=\prod _{i=1}^{3d}(\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
, where we extend
$G_{c}^{3}=\prod _{i=1}^{3d}(\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z})$
, where we extend
![]() $\unicode[STIX]{x1D706}_{i}$
periodically with period
$\unicode[STIX]{x1D706}_{i}$
periodically with period
![]() $d$
.
$d$
.
Let
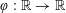 $\unicode[STIX]{x1D711}:\mathbb{R}\rightarrow \mathbb{R}$
be a fixed smooth even function supported on
$\unicode[STIX]{x1D711}:\mathbb{R}\rightarrow \mathbb{R}$
be a fixed smooth even function supported on
![]() $[-1,1]$
that equals
$[-1,1]$
that equals
![]() $1$
at the origin and whose Fourier transform
$1$
at the origin and whose Fourier transform
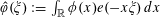 $\hat{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D709}):=\int _{\mathbb{R}}\unicode[STIX]{x1D719}(x)e(-x\unicode[STIX]{x1D709})\,dx$
is non-negative; such a function may be easily constructed by convolving an
$\hat{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D709}):=\int _{\mathbb{R}}\unicode[STIX]{x1D719}(x)e(-x\unicode[STIX]{x1D709})\,dx$
is non-negative; such a function may be easily constructed by convolving an
![]() $L^{2}$
-normalized smooth function on
$L^{2}$
-normalized smooth function on
![]() $[0,1]$
with its reflection. Let
$[0,1]$
with its reflection. Let
![]() $A\geqslant 1$
be a parameter to be chosen later, and introduce the kernel
$A\geqslant 1$
be a parameter to be chosen later, and introduce the kernel
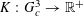 $K:G_{c}^{3}\rightarrow \mathbb{R}^{+}$
by the formula
$K:G_{c}^{3}\rightarrow \mathbb{R}^{+}$
by the formula
 $$\begin{eqnarray}K(t_{1},\ldots ,t_{3d}):=\mathop{\prod }_{i=1}^{3d}K_{i}(t_{i})\end{eqnarray}$$
$$\begin{eqnarray}K(t_{1},\ldots ,t_{3d}):=\mathop{\prod }_{i=1}^{3d}K_{i}(t_{i})\end{eqnarray}$$
for
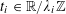 $t_{i}\in \mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}$
, where
$t_{i}\in \mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}$
, where
 $$\begin{eqnarray}K_{i}(t_{i}):=\mathop{\sum }_{k_{i}\in (1/\unicode[STIX]{x1D706}_{i})\mathbb{Z}}\unicode[STIX]{x1D711}\biggl(\frac{k_{i}}{A}\biggr)e(k_{i}t_{i}).\end{eqnarray}$$
$$\begin{eqnarray}K_{i}(t_{i}):=\mathop{\sum }_{k_{i}\in (1/\unicode[STIX]{x1D706}_{i})\mathbb{Z}}\unicode[STIX]{x1D711}\biggl(\frac{k_{i}}{A}\biggr)e(k_{i}t_{i}).\end{eqnarray}$$
By Poisson summation, the
![]() $K_{i}$
and hence
$K_{i}$
and hence
![]() $K$
are non-negative. A Fourier-analytic calculation using the smoothness of
$K$
are non-negative. A Fourier-analytic calculation using the smoothness of
![]() $\unicode[STIX]{x1D711}$
gives
$\unicode[STIX]{x1D711}$
gives
 $$\begin{eqnarray}\int _{\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}}K_{i}(t_{i})\,\frac{dt_{i}}{\unicode[STIX]{x1D706}_{i}}=1\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}}K_{i}(t_{i})\,\frac{dt_{i}}{\unicode[STIX]{x1D706}_{i}}=1\end{eqnarray}$$
and
 $$\begin{eqnarray}\int _{\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}}K_{i}(t_{i})\sin ^{2}(\unicode[STIX]{x1D70B}t_{i}/\unicode[STIX]{x1D706}_{i})\,\frac{dt_{i}}{\unicode[STIX]{x1D706}_{i}}\ll \frac{1}{A^{2}\unicode[STIX]{x1D706}_{i}^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}}K_{i}(t_{i})\sin ^{2}(\unicode[STIX]{x1D70B}t_{i}/\unicode[STIX]{x1D706}_{i})\,\frac{dt_{i}}{\unicode[STIX]{x1D706}_{i}}\ll \frac{1}{A^{2}\unicode[STIX]{x1D706}_{i}^{2}}\end{eqnarray}$$
(where the implied constant is allowed to depend on
![]() $\unicode[STIX]{x1D711}$
) and hence by (2.2) and Cauchy–Schwarz we have
$\unicode[STIX]{x1D711}$
) and hence by (2.2) and Cauchy–Schwarz we have
 $$\begin{eqnarray}\int _{\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}}K_{i}(t_{i})\Vert t_{i}\Vert _{\mathbb{R}/\mathbb{Z}}\,\frac{dt_{i}}{\unicode[STIX]{x1D706}_{i}}\ll \frac{1}{A},\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{R}/\unicode[STIX]{x1D706}_{i}\mathbb{Z}}K_{i}(t_{i})\Vert t_{i}\Vert _{\mathbb{R}/\mathbb{Z}}\,\frac{dt_{i}}{\unicode[STIX]{x1D706}_{i}}\ll \frac{1}{A},\end{eqnarray}$$
which on taking tensor products gives
 $$\begin{eqnarray}\int _{G_{c}^{3}}K(x)\,d\unicode[STIX]{x1D707}_{c}^{3}(x)=1\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{c}^{3}}K(x)\,d\unicode[STIX]{x1D707}_{c}^{3}(x)=1\end{eqnarray}$$
and
 $$\begin{eqnarray}\int _{G_{c}^{3}}K(x)\Vert x\Vert _{G_{c}^{3}}\,d\unicode[STIX]{x1D707}_{c}^{3}(x)\ll \frac{d}{A},\end{eqnarray}$$
$$\begin{eqnarray}\int _{G_{c}^{3}}K(x)\Vert x\Vert _{G_{c}^{3}}\,d\unicode[STIX]{x1D707}_{c}^{3}(x)\ll \frac{d}{A},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D707}_{c}^{3}$
is the Haar probability measure on
$\unicode[STIX]{x1D707}_{c}^{3}$
is the Haar probability measure on
![]() $G_{c}^{3}$
. If we then take the convolution
$G_{c}^{3}$
. If we then take the convolution
 $$\begin{eqnarray}\tilde{F}\ast K(x):=\int _{G_{c}}\tilde{F}(x-y)K(y)\,d\unicode[STIX]{x1D707}_{c}^{3}(y)\end{eqnarray}$$
$$\begin{eqnarray}\tilde{F}\ast K(x):=\int _{G_{c}}\tilde{F}(x-y)K(y)\,d\unicode[STIX]{x1D707}_{c}^{3}(y)\end{eqnarray}$$
then by the
![]() $1$
-Lipschitz nature of
$1$
-Lipschitz nature of
![]() $\tilde{F}$
we see that
$\tilde{F}$
we see that
 $$\begin{eqnarray}\tilde{F}\ast K(x)=\tilde{F}(x)+O\biggl(\frac{d}{A}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{F}\ast K(x)=\tilde{F}(x)+O\biggl(\frac{d}{A}\biggr).\end{eqnarray}$$
Thus, if we choose
 $$\begin{eqnarray}A:=\frac{Cd}{\unicode[STIX]{x1D702}}\end{eqnarray}$$
$$\begin{eqnarray}A:=\frac{Cd}{\unicode[STIX]{x1D702}}\end{eqnarray}$$
for a sufficiently large absolute constant
![]() $C$
, we conclude from (7.4) that
$C$
, we conclude from (7.4) that
 $$\begin{eqnarray}|\mathbb{E}(\tilde{F}\ast K(\mathbf{x}_{c})|\mathbf{c}=c)|\gg \unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(\tilde{F}\ast K(\mathbf{x}_{c})|\mathbf{c}=c)|\gg \unicode[STIX]{x1D702}.\end{eqnarray}$$
However, by Fourier expansion and the fact that
![]() $\tilde{F}$
has mean zero,
$\tilde{F}$
has mean zero,
 $$\begin{eqnarray}\tilde{F}\ast K(\mathbf{x}_{c})=\mathop{\sum }_{k\in {\hat{G}}_{c}^{3}\backslash \{0\}}\biggl(\mathop{\prod }_{i=1}^{3d}\unicode[STIX]{x1D711}\biggl(\frac{k_{i}}{A}\biggr)\biggr)\widehat{\tilde{F}(k)}\mathbb{E}e(k\cdot \mathbf{x}),\end{eqnarray}$$
$$\begin{eqnarray}\tilde{F}\ast K(\mathbf{x}_{c})=\mathop{\sum }_{k\in {\hat{G}}_{c}^{3}\backslash \{0\}}\biggl(\mathop{\prod }_{i=1}^{3d}\unicode[STIX]{x1D711}\biggl(\frac{k_{i}}{A}\biggr)\biggr)\widehat{\tilde{F}(k)}\mathbb{E}e(k\cdot \mathbf{x}),\end{eqnarray}$$
where
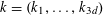 $k=(k_{1},\ldots ,k_{3d})$
with
$k=(k_{1},\ldots ,k_{3d})$
with
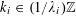 $k_{i}\in (1/\unicode[STIX]{x1D706}_{i})\mathbb{Z}$
for
$k_{i}\in (1/\unicode[STIX]{x1D706}_{i})\mathbb{Z}$
for
 $i=1,\ldots ,3d$
, and
$i=1,\ldots ,3d$
, and
 $$\begin{eqnarray}\widehat{\tilde{F}}(k):=\int _{G_{c}^{3}}\tilde{F}(x)e(-k\cdot x)\,d\unicode[STIX]{x1D707}_{c}^{3}(x).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\tilde{F}}(k):=\int _{G_{c}^{3}}\tilde{F}(x)e(-k\cdot x)\,d\unicode[STIX]{x1D707}_{c}^{3}(x).\end{eqnarray}$$
Using the triangle inequality and crudely bounding
![]() $|\widehat{\tilde{F}}(k)|$
by
$|\widehat{\tilde{F}}(k)|$
by
![]() $1$
, we conclude that
$1$
, we conclude that
 $$\begin{eqnarray}\mathop{\sum }_{k\in {\hat{G}}_{c}^{3}\backslash \{0\}}\biggl(\mathop{\prod }_{i=1}^{d}\biggl|\unicode[STIX]{x1D711}\biggl(\frac{k_{i}}{A}\biggr)\biggr|\biggr)|\mathbb{E}(e(k\cdot \mathbf{x}_{c})|\mathbf{c}=c)|\gg \unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k\in {\hat{G}}_{c}^{3}\backslash \{0\}}\biggl(\mathop{\prod }_{i=1}^{d}\biggl|\unicode[STIX]{x1D711}\biggl(\frac{k_{i}}{A}\biggr)\biggr|\biggr)|\mathbb{E}(e(k\cdot \mathbf{x}_{c})|\mathbf{c}=c)|\gg \unicode[STIX]{x1D702}.\end{eqnarray}$$
The summand is only non-vanishing when
 $\sup _{i}|k_{i}|\leqslant A$
, so that
$\sup _{i}|k_{i}|\leqslant A$
, so that
 $$\begin{eqnarray}|k|\leqslant dA\ll \exp (O(\unicode[STIX]{x1D702}^{-3C_{2}}))\end{eqnarray}$$
$$\begin{eqnarray}|k|\leqslant dA\ll \exp (O(\unicode[STIX]{x1D702}^{-3C_{2}}))\end{eqnarray}$$
(thanks to (7.5) and the choice of
![]() $A$
), and the number of such
$A$
), and the number of such
![]() $k$
is
$k$
is
 $$\begin{eqnarray}O\biggl(\mathop{\prod }_{i=1}^{3d}(A\unicode[STIX]{x1D706}_{i})\biggr)\ll \exp (O(\unicode[STIX]{x1D702}^{-3C_{2}}))\operatorname{vol}(T).\end{eqnarray}$$
$$\begin{eqnarray}O\biggl(\mathop{\prod }_{i=1}^{3d}(A\unicode[STIX]{x1D706}_{i})\biggr)\ll \exp (O(\unicode[STIX]{x1D702}^{-3C_{2}}))\operatorname{vol}(T).\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D711}$
is bounded, the claim now follows from the pigeonhole principle.◻
$\unicode[STIX]{x1D711}$
is bounded, the claim now follows from the pigeonhole principle.◻
We return to the proof of Proposition 7.1. Applying Lemma 7.2 and (6.5), we see that there exists a non-zero triplet
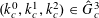 $(k_{c}^{0},k_{c}^{1},k_{c}^{2})\in {\hat{G}}_{c}^{3}$
with
$(k_{c}^{0},k_{c}^{1},k_{c}^{2})\in {\hat{G}}_{c}^{3}$
with
 $$\begin{eqnarray}|k_{c}^{0}|,|k_{c}^{1}|,|k_{c}^{2}|\ll \exp (\unicode[STIX]{x1D702}^{-3C_{2}})\end{eqnarray}$$
$$\begin{eqnarray}|k_{c}^{0}|,|k_{c}^{1}|,|k_{c}^{2}|\ll \exp (\unicode[STIX]{x1D702}^{-3C_{2}})\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathbb{E}(e(k_{c}^{0}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a})+k_{c}^{1}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}\,+\,\mathbf{r})+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r}))|\mathbf{c}=c)\gg \exp (-\unicode[STIX]{x1D702}^{-3C_{3}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}(e(k_{c}^{0}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a})+k_{c}^{1}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}\,+\,\mathbf{r})+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+2\mathbf{r}))|\mathbf{c}=c)\gg \exp (-\unicode[STIX]{x1D702}^{-3C_{3}}).\end{eqnarray}$$
Among other things, the non-zero nature of this triplet forces
![]() $G_{c}$
to be non-trivial, and thus
$G_{c}$
to be non-trivial, and thus
 $$\begin{eqnarray}d_{2}^{\text{poor}}(v)\geqslant 1.\end{eqnarray}$$
$$\begin{eqnarray}d_{2}^{\text{poor}}(v)\geqslant 1.\end{eqnarray}$$
We also emphasize that the bound (7.6) involves
![]() $C_{2}$
rather than
$C_{2}$
rather than
![]() $C_{3}$
; this will become important when establishing the important upper bound of (7.2) later in this proof.
$C_{3}$
; this will become important when establishing the important upper bound of (7.2) later in this proof.
We can use the exponential sum bound (7.7) to control the “second derivative” of
![]() $\unicode[STIX]{x1D6EF}_{c}$
. Indeed, for any
$\unicode[STIX]{x1D6EF}_{c}$
. Indeed, for any
 $h_{1},h_{2}\in B(S_{c},\unicode[STIX]{x1D70C}_{c}/10)$
, define the quantity
$h_{1},h_{2}\in B(S_{c},\unicode[STIX]{x1D70C}_{c}/10)$
, define the quantity
 $\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(h_{1},h_{2})\in \mathbb{R}/\mathbb{Z}$
by
$\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(h_{1},h_{2})\in \mathbb{R}/\mathbb{Z}$
by
 $$\begin{eqnarray}\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(h_{1},h_{2}):=\unicode[STIX]{x1D6EF}_{c}(a+h_{1}+h_{2})-\unicode[STIX]{x1D6EF}_{c}(a+h_{1})-\unicode[STIX]{x1D6EF}_{c}(a+h_{2})+\unicode[STIX]{x1D6EF}_{c}(a)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(h_{1},h_{2}):=\unicode[STIX]{x1D6EF}_{c}(a+h_{1}+h_{2})-\unicode[STIX]{x1D6EF}_{c}(a+h_{1})-\unicode[STIX]{x1D6EF}_{c}(a+h_{2})+\unicode[STIX]{x1D6EF}_{c}(a)\end{eqnarray}$$
for any
 $a\in n_{c}+B(S_{c},\unicode[STIX]{x1D70C}/2)$
. Since
$a\in n_{c}+B(S_{c},\unicode[STIX]{x1D70C}/2)$
. Since
![]() $\unicode[STIX]{x1D6E4}_{\mathbf{c}}$
is locally quadratic on
$\unicode[STIX]{x1D6E4}_{\mathbf{c}}$
is locally quadratic on
 $n_{c}+B(S_{c},\unicode[STIX]{x1D70C})$
, this quantity is well-defined, symmetric in
$n_{c}+B(S_{c},\unicode[STIX]{x1D70C})$
, this quantity is well-defined, symmetric in
![]() $h_{1},h_{2}$
, and is also locally bilinear in
$h_{1},h_{2}$
, and is also locally bilinear in
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
.
$h_{2}$
.
Lemma 7.3. Let the notation and hypotheses be as above. Then for any
 $i=0,1,2$
, we have
$i=0,1,2$
, we have
 $$\begin{eqnarray}|\mathbb{E}(e(2k_{c}^{i}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(\mathbf{r}-\mathbf{r}^{\prime },\mathbf{h}-\mathbf{h}^{\prime }))|\mathbf{c}=c)|\gg \exp (-4\unicode[STIX]{x1D702}^{-3C_{3}}),\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(e(2k_{c}^{i}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(\mathbf{r}-\mathbf{r}^{\prime },\mathbf{h}-\mathbf{h}^{\prime }))|\mathbf{c}=c)|\gg \exp (-4\unicode[STIX]{x1D702}^{-3C_{3}}),\end{eqnarray}$$
where, conditioning on the event
![]() $\mathbf{c}=c$
, the random variables
$\mathbf{c}=c$
, the random variables
 $\mathbf{r},\mathbf{r}^{\prime },\mathbf{h},\mathbf{h}^{\prime }$
are drawn independently and regularly from the Bohr sets
$\mathbf{r},\mathbf{r}^{\prime },\mathbf{h},\mathbf{h}^{\prime }$
are drawn independently and regularly from the Bohr sets
 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C})$
,
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C})$
,
 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C})$
,
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C})$
,
 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C})$
,
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C})$
,
 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C})$
respectively, independently of
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C})$
respectively, independently of
![]() $\mathbf{a}$
.
$\mathbf{a}$
.
Proof. To simplify the notation we only consider the
![]() $i=2$
case, as the
$i=2$
case, as the
![]() $i=0,1$
cases are similar. This will be “Weyl differencing” argument that relies primarily on the Cauchy–Schwarz inequality.
$i=0,1$
cases are similar. This will be “Weyl differencing” argument that relies primarily on the Cauchy–Schwarz inequality.
Recall that after conditioning to the event
![]() $\mathbf{c}=c$
, the random variable
$\mathbf{c}=c$
, the random variable
![]() $\mathbf{a}$
is drawn regularly from
$\mathbf{a}$
is drawn regularly from
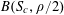 $B(S_{c},\unicode[STIX]{x1D70C}/2)$
. Using Lemma 4.4, we see that
$B(S_{c},\unicode[STIX]{x1D70C}/2)$
. Using Lemma 4.4, we see that
![]() $\mathbf{a}$
and
$\mathbf{a}$
and
![]() $\mathbf{a}-\mathbf{h}$
differ in total variation by
$\mathbf{a}-\mathbf{h}$
differ in total variation by
 $O(\exp (-\unicode[STIX]{x1D702}^{-C_{4}/2}))$
, hence from (7.7) we have
$O(\exp (-\unicode[STIX]{x1D702}^{-C_{4}/2}))$
, hence from (7.7) we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}(e(k_{c}^{0}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}-\mathbf{h})+k_{c}^{1}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}-\mathbf{h}+\mathbf{r})+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}-\mathbf{h}+2\mathbf{r}))|\mathbf{c}=c)|\nonumber\\ \displaystyle & & \displaystyle \quad \gg \exp (-\unicode[STIX]{x1D702}^{-3C_{3}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}(e(k_{c}^{0}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}-\mathbf{h})+k_{c}^{1}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}-\mathbf{h}+\mathbf{r})+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}-\mathbf{h}+2\mathbf{r}))|\mathbf{c}=c)|\nonumber\\ \displaystyle & & \displaystyle \quad \gg \exp (-\unicode[STIX]{x1D702}^{-3C_{3}}).\nonumber\end{eqnarray}$$
Similarly we may use Lemma 4.4 to compare
![]() $\mathbf{r}$
and
$\mathbf{r}$
and
![]() $\mathbf{r}+\mathbf{h}$
, and conclude that
$\mathbf{r}+\mathbf{h}$
, and conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}(e(k_{c}^{0}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}-\mathbf{h})+k_{c}^{1}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r})+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{h}+2\mathbf{r}))|\mathbf{c}=c)|\nonumber\\ \displaystyle & & \displaystyle \quad \gg \exp (-\unicode[STIX]{x1D702}^{-3C_{3}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}(e(k_{c}^{0}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}-\mathbf{h})+k_{c}^{1}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{r})+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(\mathbf{a}+\mathbf{h}+2\mathbf{r}))|\mathbf{c}=c)|\nonumber\\ \displaystyle & & \displaystyle \quad \gg \exp (-\unicode[STIX]{x1D702}^{-3C_{3}}).\nonumber\end{eqnarray}$$
By the pigeonhole principle (and independence of
![]() $\mathbf{a},\mathbf{h},\mathbf{r}$
relative to the event
$\mathbf{a},\mathbf{h},\mathbf{r}$
relative to the event
![]() $\mathbf{c}=c$
), we may thus find
$\mathbf{c}=c$
), we may thus find
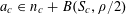 $a_{c}\in n_{c}+B(S_{c},\unicode[STIX]{x1D70C}/2)$
such that
$a_{c}\in n_{c}+B(S_{c},\unicode[STIX]{x1D70C}/2)$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}(e(k_{c}^{0}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}-\mathbf{h})+k_{c}^{1}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}+\mathbf{r})+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}+\mathbf{h}+2\mathbf{r}))|\mathbf{c}=c)|\nonumber\\ \displaystyle & & \displaystyle \quad \gg \exp (-\unicode[STIX]{x1D702}^{-3C_{3}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}(e(k_{c}^{0}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}-\mathbf{h})+k_{c}^{1}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}+\mathbf{r})+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}+\mathbf{h}+2\mathbf{r}))|\mathbf{c}=c)|\nonumber\\ \displaystyle & & \displaystyle \quad \gg \exp (-\unicode[STIX]{x1D702}^{-3C_{3}}).\nonumber\end{eqnarray}$$
Using the identity
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{c}(a_{c}+\mathbf{h}+2\mathbf{r})=\unicode[STIX]{x1D6EF}_{c}(a_{c}+\mathbf{h})+\unicode[STIX]{x1D6EF}_{c}(a_{c}+2\mathbf{r})-\unicode[STIX]{x1D6EF}_{c}(a_{c})+\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(2\mathbf{r},\mathbf{h})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{c}(a_{c}+\mathbf{h}+2\mathbf{r})=\unicode[STIX]{x1D6EF}_{c}(a_{c}+\mathbf{h})+\unicode[STIX]{x1D6EF}_{c}(a_{c}+2\mathbf{r})-\unicode[STIX]{x1D6EF}_{c}(a_{c})+\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(2\mathbf{r},\mathbf{h})\end{eqnarray}$$
we can rewrite the left-hand side as
 $$\begin{eqnarray}|\mathbb{E}(b_{1}(\mathbf{r})b_{2}(\mathbf{h})e(k_{c}^{2}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(2\mathbf{r},\mathbf{h}))|\mathbf{c}=c)|\gg \exp (-\unicode[STIX]{x1D702}^{-3C_{3}})\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(b_{1}(\mathbf{r})b_{2}(\mathbf{h})e(k_{c}^{2}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(2\mathbf{r},\mathbf{h}))|\mathbf{c}=c)|\gg \exp (-\unicode[STIX]{x1D702}^{-3C_{3}})\end{eqnarray}$$
where
 $b_{1},b_{2}:B(S_{c},\unicode[STIX]{x1D70C})\rightarrow \mathbb{C}$
are the
$b_{1},b_{2}:B(S_{c},\unicode[STIX]{x1D70C})\rightarrow \mathbb{C}$
are the
![]() $1$
-bounded functions
$1$
-bounded functions
 $$\begin{eqnarray}b_{1}(r):=e(k_{c}^{1}\cdot \unicode[STIX]{x1D6EF}_{\mathbf{c}}(a_{c}+r)+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}+2r)-k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}))\end{eqnarray}$$
$$\begin{eqnarray}b_{1}(r):=e(k_{c}^{1}\cdot \unicode[STIX]{x1D6EF}_{\mathbf{c}}(a_{c}+r)+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}+2r)-k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}))\end{eqnarray}$$
and
 $$\begin{eqnarray}b_{2}(h):=e(k_{c}^{0}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}-h)+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}+h)).\end{eqnarray}$$
$$\begin{eqnarray}b_{2}(h):=e(k_{c}^{0}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}-h)+k_{c}^{2}\cdot \unicode[STIX]{x1D6EF}_{c}(a_{c}+h)).\end{eqnarray}$$
Applying Lemma 2.1 to eliminate the
![]() $\mathbf{b}_{1}(\mathbf{r})$
factor, we conclude that
$\mathbf{b}_{1}(\mathbf{r})$
factor, we conclude that
 $$\begin{eqnarray}|\mathbb{E}(b_{2}(\mathbf{h})\overline{b_{2}(\mathbf{h}^{\prime })}e(k_{c}^{2}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(2\mathbf{r},\mathbf{h}-\mathbf{h}^{\prime }))|\mathbf{c}=c)|\gg \exp (-2\unicode[STIX]{x1D702}^{-3C_{3}}).\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(b_{2}(\mathbf{h})\overline{b_{2}(\mathbf{h}^{\prime })}e(k_{c}^{2}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(2\mathbf{r},\mathbf{h}-\mathbf{h}^{\prime }))|\mathbf{c}=c)|\gg \exp (-2\unicode[STIX]{x1D702}^{-3C_{3}}).\end{eqnarray}$$
Applying Lemma 2.1 again to eliminate the
 $b_{2}(\mathbf{h})\overline{b_{2}(\mathbf{h}^{\prime })}$
factor, we obtain the claim.◻
$b_{2}(\mathbf{h})\overline{b_{2}(\mathbf{h}^{\prime })}$
factor, we obtain the claim.◻
We return to the proof of Proposition 7.1. Let
 $i=i_{c}\in \{0,1,2\}$
be such that
$i=i_{c}\in \{0,1,2\}$
be such that
![]() $k_{c}^{i}$
is non-zero. Let
$k_{c}^{i}$
is non-zero. Let
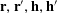 $\mathbf{r},\mathbf{r}^{\prime },\mathbf{h},\mathbf{h}^{\prime }$
be as in the above lemma, and let
$\mathbf{r},\mathbf{r}^{\prime },\mathbf{h},\mathbf{h}^{\prime }$
be as in the above lemma, and let
![]() $\mathbf{h}^{\prime \prime }$
be a further independent copy of
$\mathbf{h}^{\prime \prime }$
be a further independent copy of
![]() $\mathbf{h}$
or
$\mathbf{h}$
or
![]() $\mathbf{h}^{\prime }$
, thus
$\mathbf{h}^{\prime }$
, thus
![]() $\mathbf{h}^{\prime \prime }$
is also drawn regularly from
$\mathbf{h}^{\prime \prime }$
is also drawn regularly from
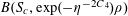 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C})$
and independently of
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C})$
and independently of
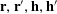 $\mathbf{r},\mathbf{r}^{\prime },\mathbf{h},\mathbf{h}^{\prime }$
(after conditioning on
$\mathbf{r},\mathbf{r}^{\prime },\mathbf{h},\mathbf{h}^{\prime }$
(after conditioning on
![]() $\mathbf{c}=c$
). Applying Lemma 4.4 to compare
$\mathbf{c}=c$
). Applying Lemma 4.4 to compare
![]() $\mathbf{r}$
with
$\mathbf{r}$
with
![]() $\mathbf{r}+\mathbf{h}^{\prime \prime }$
, we have
$\mathbf{r}+\mathbf{h}^{\prime \prime }$
, we have
 $$\begin{eqnarray}|\mathbb{E}(e(2k_{c}^{i}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(\mathbf{r}-\mathbf{r}^{\prime }+\mathbf{h}^{\prime \prime },\mathbf{h}-\mathbf{h}^{\prime }))|\mathbf{c}=c)|\gg \exp (-4\unicode[STIX]{x1D702}^{-3C_{3}}),\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(e(2k_{c}^{i}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(\mathbf{r}-\mathbf{r}^{\prime }+\mathbf{h}^{\prime \prime },\mathbf{h}-\mathbf{h}^{\prime }))|\mathbf{c}=c)|\gg \exp (-4\unicode[STIX]{x1D702}^{-3C_{3}}),\end{eqnarray}$$
so by the pigeonhole principle we can find
 $r,r^{\prime },h^{\prime }\in B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C}_{c})$
(depending on
$r,r^{\prime },h^{\prime }\in B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C}_{c})$
(depending on
![]() $c$
, of course) such that
$c$
, of course) such that
 $$\begin{eqnarray}|\mathbb{E}(e(2k_{c}^{i}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(r-r^{\prime }+\mathbf{h}^{\prime \prime },\mathbf{h}-h^{\prime }))|\mathbf{c}=c)|\gg \exp (-4\unicode[STIX]{x1D702}^{-3C_{3}}).\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(e(2k_{c}^{i}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(r-r^{\prime }+\mathbf{h}^{\prime \prime },\mathbf{h}-h^{\prime }))|\mathbf{c}=c)|\gg \exp (-4\unicode[STIX]{x1D702}^{-3C_{3}}).\end{eqnarray}$$
By the local bilinearity of
![]() $\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}$
, we may thus have
$\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}$
, we may thus have
 $$\begin{eqnarray}|\mathbb{E}(e(2k_{c}^{i}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(\mathbf{h}^{\prime \prime },\mathbf{h})+\unicode[STIX]{x1D713}(\mathbf{h})+\unicode[STIX]{x1D713}^{\prime \prime }(\mathbf{h}^{\prime \prime }))|\mathbf{c}=c)|\gg \exp (-4\unicode[STIX]{x1D702}^{-3C_{3}})\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(e(2k_{c}^{i}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(\mathbf{h}^{\prime \prime },\mathbf{h})+\unicode[STIX]{x1D713}(\mathbf{h})+\unicode[STIX]{x1D713}^{\prime \prime }(\mathbf{h}^{\prime \prime }))|\mathbf{c}=c)|\gg \exp (-4\unicode[STIX]{x1D702}^{-3C_{3}})\end{eqnarray}$$
for some locally linear functions
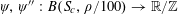 $\unicode[STIX]{x1D713},\unicode[STIX]{x1D713}^{\prime \prime }:B(S_{c},\unicode[STIX]{x1D70C}/100)\rightarrow \mathbb{R}/\mathbb{Z}$
(which can depend on
$\unicode[STIX]{x1D713},\unicode[STIX]{x1D713}^{\prime \prime }:B(S_{c},\unicode[STIX]{x1D70C}/100)\rightarrow \mathbb{R}/\mathbb{Z}$
(which can depend on
![]() $c$
).
$c$
).
Applying Proposition 4.11 (recalling from (6.3) that
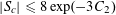 $|S_{c}|\leqslant 8\exp (-3C_{2})$
), we conclude that there exists a non-zero multiple
$|S_{c}|\leqslant 8\exp (-3C_{2})$
), we conclude that there exists a non-zero multiple
![]() $k_{c}\in {\hat{G}}_{c}$
of
$k_{c}\in {\hat{G}}_{c}$
of
![]() $k_{c}^{i}$
with
$k_{c}^{i}$
with
 $$\begin{eqnarray}k_{c}\ll \exp (\unicode[STIX]{x1D702}^{-4C_{3}})\end{eqnarray}$$
$$\begin{eqnarray}k_{c}\ll \exp (\unicode[STIX]{x1D702}^{-4C_{3}})\end{eqnarray}$$
such that
 $$\begin{eqnarray}\Vert k_{c}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(n,m)\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (\unicode[STIX]{x1D702}^{-3C_{4}})\frac{\Vert n\Vert _{S_{c}}\Vert m\Vert _{S_{c}}}{\unicode[STIX]{x1D70C}_{c}^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert k_{c}\cdot \unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D6EF}_{c}(n,m)\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (\unicode[STIX]{x1D702}^{-3C_{4}})\frac{\Vert n\Vert _{S_{c}}\Vert m\Vert _{S_{c}}}{\unicode[STIX]{x1D70C}_{c}^{2}}\end{eqnarray}$$
for
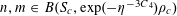 $n,m\in B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-3C_{4}})\unicode[STIX]{x1D70C}_{c})$
.
$n,m\in B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-3C_{4}})\unicode[STIX]{x1D70C}_{c})$
.
Applying Corollary 4.13, we may thus find
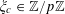 $\unicode[STIX]{x1D709}_{c}\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}_{c}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\biggl\|k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(n_{c}+h)-k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(n_{c})-\frac{\unicode[STIX]{x1D709}_{c}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\ll \exp (\unicode[STIX]{x1D702}^{-4C_{4}})\frac{\Vert h\Vert _{S_{c}}}{\unicode[STIX]{x1D70C}_{c}}\end{eqnarray}$$
$$\begin{eqnarray}\biggl\|k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(n_{c}+h)-k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(n_{c})-\frac{\unicode[STIX]{x1D709}_{c}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\ll \exp (\unicode[STIX]{x1D702}^{-4C_{4}})\frac{\Vert h\Vert _{S_{c}}}{\unicode[STIX]{x1D70C}_{c}}\end{eqnarray}$$
for all
 $n\in \mathbb{Z}/p\mathbb{Z}$
(of course, the bound is only non-trivial when
$n\in \mathbb{Z}/p\mathbb{Z}$
(of course, the bound is only non-trivial when
![]() $h$
lies in the Bohr set
$h$
lies in the Bohr set
 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\unicode[STIX]{x1D70C})$
).
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\unicode[STIX]{x1D70C})$
).
The dual frequency
![]() $k_{c}\in \widehat{G_{c}}$
is non-zero, but not necessarily irreducible. However, we may write
$k_{c}\in \widehat{G_{c}}$
is non-zero, but not necessarily irreducible. However, we may write
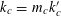 $k_{c}=m_{c}k_{c}^{\prime }$
where
$k_{c}=m_{c}k_{c}^{\prime }$
where
![]() $m_{c}$
is a positive natural number and
$m_{c}$
is a positive natural number and
![]() $k_{c}^{\prime }\in \widehat{G_{c}}$
is irreducible, thus by (7.8) we have the bound (7.1). The same argument gives the bound
$k_{c}^{\prime }\in \widehat{G_{c}}$
is irreducible, thus by (7.8) we have the bound (7.1). The same argument gives the bound
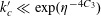 $k_{c}^{\prime }\ll \exp (\unicode[STIX]{x1D702}^{-4C_{3}})$
, but this is not sufficient to establish the upper bound in (7.2). However, observe that
$k_{c}^{\prime }\ll \exp (\unicode[STIX]{x1D702}^{-4C_{3}})$
, but this is not sufficient to establish the upper bound in (7.2). However, observe that
![]() $k_{c}^{i}$
must also be a multiple of the irreducible vector
$k_{c}^{i}$
must also be a multiple of the irreducible vector
![]() $k_{c}^{\prime }$
, and now the upper bound in (7.2) follows from (7.6).
$k_{c}^{\prime }$
, and now the upper bound in (7.2) follows from (7.6).
We can also obtain a lower bound on
![]() $k_{c}^{\prime }$
by observing that the slab
$k_{c}^{\prime }$
by observing that the slab
 $$\begin{eqnarray}\{x\in G_{c}:\Vert k_{c}^{\prime }\cdot x\Vert _{\mathbb{ R}/\mathbb{Z}}\leqslant {\textstyle \frac{1}{2}}|k_{c}^{\prime }|\}\end{eqnarray}$$
$$\begin{eqnarray}\{x\in G_{c}:\Vert k_{c}^{\prime }\cdot x\Vert _{\mathbb{ R}/\mathbb{Z}}\leqslant {\textstyle \frac{1}{2}}|k_{c}^{\prime }|\}\end{eqnarray}$$
has measure at most
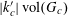 $|k_{c}^{\prime }|\operatorname{vol}(G_{c})$
, and contains the Euclidean ball of radius
$|k_{c}^{\prime }|\operatorname{vol}(G_{c})$
, and contains the Euclidean ball of radius
![]() $1/2$
centred at the origin. This gives the lower bound
$1/2$
centred at the origin. This gives the lower bound
 $$\begin{eqnarray}|k_{c}^{\prime }|\gg \frac{1}{\dim (G_{c})^{O(\dim (G_{c}))}\operatorname{vol}(G_{c})}\end{eqnarray}$$
$$\begin{eqnarray}|k_{c}^{\prime }|\gg \frac{1}{\dim (G_{c})^{O(\dim (G_{c}))}\operatorname{vol}(G_{c})}\end{eqnarray}$$
which by (6.4), (6.6) gives the lower bound in (7.2).
Now let
 $a\in B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
and
$a\in B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
and
 $h\in B(S_{c}\cup \{\unicode[STIX]{x1D709}_{c}\},\exp (-\unicode[STIX]{x1D702}^{-5C_{4}})\unicode[STIX]{x1D70C}_{c})$
. Then we have
$h\in B(S_{c}\cup \{\unicode[STIX]{x1D709}_{c}\},\exp (-\unicode[STIX]{x1D702}^{-5C_{4}})\unicode[STIX]{x1D70C}_{c})$
. Then we have
 $$\begin{eqnarray}jh\in B(S_{c},2m_{c}\exp (-\unicode[STIX]{x1D702}^{-5C_{4}})\unicode[STIX]{x1D70C}_{c})\end{eqnarray}$$
$$\begin{eqnarray}jh\in B(S_{c},2m_{c}\exp (-\unicode[STIX]{x1D702}^{-5C_{4}})\unicode[STIX]{x1D70C}_{c})\end{eqnarray}$$
and
 $$\begin{eqnarray}\biggl\|\frac{j\unicode[STIX]{x1D709}_{c}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-5C_{4}})\unicode[STIX]{x1D70C}_{c}\end{eqnarray}$$
$$\begin{eqnarray}\biggl\|\frac{j\unicode[STIX]{x1D709}_{c}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-5C_{4}})\unicode[STIX]{x1D70C}_{c}\end{eqnarray}$$
for all
![]() $j$
,
$j$
,
 $0\leqslant j\leqslant 2m_{c}$
. From (7.10) and (7.1), we conclude that
$0\leqslant j\leqslant 2m_{c}$
. From (7.10) and (7.1), we conclude that
 $$\begin{eqnarray}\Vert k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(n_{c}+jh)-k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(n_{c})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\end{eqnarray}$$
$$\begin{eqnarray}\Vert k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(n_{c}+jh)-k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(n_{c})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\end{eqnarray}$$
(for example). On the other hand, from (7.9) we have
 $$\begin{eqnarray}\Vert k_{c}\cdot (\unicode[STIX]{x1D6EF}_{c}(a+jh)-\unicode[STIX]{x1D6EF}_{c}(a)-\unicode[STIX]{x1D6EF}_{c}(n_{c}+j\unicode[STIX]{x1D709}_{c}h)+\unicode[STIX]{x1D6EF}_{c}(n_{c}))\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\end{eqnarray}$$
$$\begin{eqnarray}\Vert k_{c}\cdot (\unicode[STIX]{x1D6EF}_{c}(a+jh)-\unicode[STIX]{x1D6EF}_{c}(a)-\unicode[STIX]{x1D6EF}_{c}(n_{c}+j\unicode[STIX]{x1D709}_{c}h)+\unicode[STIX]{x1D6EF}_{c}(n_{c}))\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\end{eqnarray}$$
and hence by the triangle inequality we have
 $$\begin{eqnarray}\Vert k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(a+jh)-k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(a)\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\end{eqnarray}$$
$$\begin{eqnarray}\Vert k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(a+jh)-k_{c}\cdot \unicode[STIX]{x1D6EF}_{c}(a)\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\end{eqnarray}$$
for all
![]() $j$
,
$j$
,
 $0\leqslant j\leqslant 2m_{c}$
.
$0\leqslant j\leqslant 2m_{c}$
.
This is close to (7.3), but we will need to replace the dual frequency
![]() $k_{c}$
here with the irreducible dual frequency
$k_{c}$
here with the irreducible dual frequency
![]() $k_{c}^{\prime }$
. To do this, we first observe that as
$k_{c}^{\prime }$
. To do this, we first observe that as
![]() $\unicode[STIX]{x1D6EF}_{c}$
is locally quadratic on
$\unicode[STIX]{x1D6EF}_{c}$
is locally quadratic on
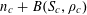 $n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})$
, we may write
$n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})$
, we may write
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{c}(a+jh)=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}j+\unicode[STIX]{x1D6FE}j^{2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{c}(a+jh)=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}j+\unicode[STIX]{x1D6FE}j^{2}\end{eqnarray}$$
for all
![]() $j$
,
$j$
,
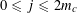 $0\leqslant j\leqslant 2m_{c}$
, and some
$0\leqslant j\leqslant 2m_{c}$
, and some
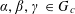 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in G_{c}$
depending on
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in G_{c}$
depending on
![]() $c,a,h$
. Inserting this formula into the preceding estimate, we conclude that
$c,a,h$
. Inserting this formula into the preceding estimate, we conclude that
 $$\begin{eqnarray}\Vert j(k_{c}\cdot \unicode[STIX]{x1D6FD})+j^{2}(k_{c}\cdot \unicode[STIX]{x1D6FE})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\end{eqnarray}$$
$$\begin{eqnarray}\Vert j(k_{c}\cdot \unicode[STIX]{x1D6FD})+j^{2}(k_{c}\cdot \unicode[STIX]{x1D6FE})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\end{eqnarray}$$
for
![]() $j$
,
$j$
,
 $0\leqslant j\leqslant 2m_{c}$
. Applying this for
$0\leqslant j\leqslant 2m_{c}$
. Applying this for
![]() $j=1,2$
and using the triangle inequality, we have
$j=1,2$
and using the triangle inequality, we have
 $$\begin{eqnarray}\Vert k_{c}\cdot \unicode[STIX]{x1D6FD}\Vert ,\Vert 2(k_{c}\cdot \unicode[STIX]{x1D6FE})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-4C_{4}}).\end{eqnarray}$$
$$\begin{eqnarray}\Vert k_{c}\cdot \unicode[STIX]{x1D6FD}\Vert ,\Vert 2(k_{c}\cdot \unicode[STIX]{x1D6FE})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-4C_{4}}).\end{eqnarray}$$
Since
 $2m_{c}k_{c}^{\prime }=2k_{c}$
and
$2m_{c}k_{c}^{\prime }=2k_{c}$
and
 $(2m_{c})^{2}k_{c}^{\prime }=(2m_{c})2k_{c}$
, we conclude in particular (using (7.1)) that
$(2m_{c})^{2}k_{c}^{\prime }=(2m_{c})2k_{c}$
, we conclude in particular (using (7.1)) that
 $$\begin{eqnarray}\Vert 2m_{c}(k_{c}^{\prime }\cdot \unicode[STIX]{x1D6FD})\Vert _{\mathbb{ R}/\mathbb{Z}},\Vert (2m_{c})^{2}(k_{c}^{\prime }\cdot \unicode[STIX]{x1D6FE})\Vert _{\mathbb{ R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-3C_{4}})\end{eqnarray}$$
$$\begin{eqnarray}\Vert 2m_{c}(k_{c}^{\prime }\cdot \unicode[STIX]{x1D6FD})\Vert _{\mathbb{ R}/\mathbb{Z}},\Vert (2m_{c})^{2}(k_{c}^{\prime }\cdot \unicode[STIX]{x1D6FE})\Vert _{\mathbb{ R}/\mathbb{Z}}\ll \exp (-\unicode[STIX]{x1D702}^{-3C_{4}})\end{eqnarray}$$
and thus by (7.12) we obtain (7.3) as desired. This finally completes the proof of Proposition 7.1. ◻
We now return to the proof of Theorem 6.7. We are given a structured local approximant
 $$\begin{eqnarray}v=(C,\mathbf{c},(n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}))_{c\in C},(G_{c})_{c\in C},(F_{c})_{c\in C},(\unicode[STIX]{x1D6EF}_{c})_{c\in C})\end{eqnarray}$$
$$\begin{eqnarray}v=(C,\mathbf{c},(n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}))_{c\in C},(G_{c})_{c\in C},(F_{c})_{c\in C},(\unicode[STIX]{x1D6EF}_{c})_{c\in C})\end{eqnarray}$$
and need to construct a modification
 $$\begin{eqnarray}v^{\prime }=(C^{\prime },\mathbf{c}^{\prime },(n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }))_{c^{\prime }\in C^{\prime }},(G_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(F_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }})\end{eqnarray}$$
$$\begin{eqnarray}v^{\prime }=(C^{\prime },\mathbf{c}^{\prime },(n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }))_{c^{\prime }\in C^{\prime }},(G_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(F_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }})\end{eqnarray}$$
that somehow incorporates the linear constraint identified in Proposition 7.1 to decrement the poorly distributed quadratic dimension of
![]() $v^{\prime }$
, in the spirit of the third and fourth examples in §3. To avoid confusion, we shall restore the subscripts
$v^{\prime }$
, in the spirit of the third and fourth examples in §3. To avoid confusion, we shall restore the subscripts
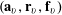 $(\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v})$
on the random variables associated to
$(\mathbf{a}_{v},\mathbf{r}_{v},\mathbf{f}_{v})$
on the random variables associated to
![]() $v$
as per Definition 6.1, to distinguish them from the corresponding random variables
$v$
as per Definition 6.1, to distinguish them from the corresponding random variables
 $(\mathbf{a}_{v^{\prime }},\mathbf{r}_{v^{\prime }},\mathbf{f}_{v^{\prime }})$
that will be associated to
$(\mathbf{a}_{v^{\prime }},\mathbf{r}_{v^{\prime }},\mathbf{f}_{v^{\prime }})$
that will be associated to
![]() $v^{\prime }$
.
$v^{\prime }$
.
We shall set
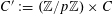 $C^{\prime }:=(\mathbb{Z}/p\mathbb{Z})\times C$
, and let
$C^{\prime }:=(\mathbb{Z}/p\mathbb{Z})\times C$
, and let
![]() $\mathbf{c}^{\prime }$
be the random variable
$\mathbf{c}^{\prime }$
be the random variable
 $$\begin{eqnarray}\mathbf{c}^{\prime }:=(\mathbf{a}_{v},\mathbf{c}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{c}^{\prime }:=(\mathbf{a}_{v},\mathbf{c}).\end{eqnarray}$$
Clearly
![]() $\mathbf{c}^{\prime }$
takes values in the non-empty finite set
$\mathbf{c}^{\prime }$
takes values in the non-empty finite set
![]() $C^{\prime }$
. Now we need to define
$C^{\prime }$
. Now we need to define
 $n_{c^{\prime }}^{\prime },S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime },G_{c^{\prime }}^{\prime },F_{c^{\prime }}^{\prime },\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }$
for any given
$n_{c^{\prime }}^{\prime },S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime },G_{c^{\prime }}^{\prime },F_{c^{\prime }}^{\prime },\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }$
for any given
 $c^{\prime }=(a,c)$
in
$c^{\prime }=(a,c)$
in
![]() $C^{\prime }$
. In the case where
$C^{\prime }$
. In the case where
![]() $c$
is not poorly distributed, we simply carry over the corresponding data from
$c$
is not poorly distributed, we simply carry over the corresponding data from
![]() $v$
without further modification. That is to say, we define
$v$
without further modification. That is to say, we define
 $$\begin{eqnarray}(n_{c^{\prime }}^{\prime },S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime },G_{c^{\prime }}^{\prime },F_{c^{\prime }}^{\prime },\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }):=(n_{c},S_{c},\unicode[STIX]{x1D70C}_{c},G_{c},F_{c},\unicode[STIX]{x1D6EF}_{c})\end{eqnarray}$$
$$\begin{eqnarray}(n_{c^{\prime }}^{\prime },S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime },G_{c^{\prime }}^{\prime },F_{c^{\prime }}^{\prime },\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }):=(n_{c},S_{c},\unicode[STIX]{x1D70C}_{c},G_{c},F_{c},\unicode[STIX]{x1D6EF}_{c})\end{eqnarray}$$
whenever
 $c^{\prime }=(a,c)$
with
$c^{\prime }=(a,c)$
with
![]() $c$
not poorly distributed. If instead
$c$
not poorly distributed. If instead
 $c^{\prime }=(a,c)$
with
$c^{\prime }=(a,c)$
with
![]() $c$
poorly distributed, then we introduce the natural number
$c$
poorly distributed, then we introduce the natural number
![]() $m_{c}$
, the dual frequency
$m_{c}$
, the dual frequency
![]() $k_{c}^{\prime }\in {\hat{G}}_{c}$
, and the frequency
$k_{c}^{\prime }\in {\hat{G}}_{c}$
, and the frequency
 $\unicode[STIX]{x1D709}_{c}\in \mathbb{Z}/p\mathbb{Z}$
from Proposition 7.1; of course we can arrange matters so that
$\unicode[STIX]{x1D709}_{c}\in \mathbb{Z}/p\mathbb{Z}$
from Proposition 7.1; of course we can arrange matters so that
 $m_{c},k_{c}^{\prime },\unicode[STIX]{x1D709}_{c}$
depend only on
$m_{c},k_{c}^{\prime },\unicode[STIX]{x1D709}_{c}$
depend only on
![]() $c$
and not on
$c$
and not on
![]() $a$
. Because of (7.1) and the hypothesis (3.21), the quantity
$a$
. Because of (7.1) and the hypothesis (3.21), the quantity
![]() $2m_{c}$
is invertible in the field
$2m_{c}$
is invertible in the field
![]() $\mathbb{Z}/p\mathbb{Z}$
, and so we may define the dilate
$\mathbb{Z}/p\mathbb{Z}$
, and so we may define the dilate
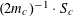 $(2m_{c})^{-1}\cdot S_{c}$
of
$(2m_{c})^{-1}\cdot S_{c}$
of
![]() $S_{c}$
inside
$S_{c}$
inside
![]() $\mathbb{Z}/p\mathbb{Z}$
, and can similarly define the dilate
$\mathbb{Z}/p\mathbb{Z}$
, and can similarly define the dilate
 $(2m_{c})^{-1}\unicode[STIX]{x1D709}_{c}$
of
$(2m_{c})^{-1}\unicode[STIX]{x1D709}_{c}$
of
![]() $\unicode[STIX]{x1D709}_{c}$
. We will need to do this division here to cancel some denominators appearing later in the argument.
$\unicode[STIX]{x1D709}_{c}$
. We will need to do this division here to cancel some denominators appearing later in the argument.
In this poorly distributed case, we define the “linear” data
 $n_{c^{\prime }}^{\prime },S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }$
by
$n_{c^{\prime }}^{\prime },S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }$
by
 $$\begin{eqnarray}\displaystyle n_{c^{\prime }}^{\prime } & := & \displaystyle a,\nonumber\\ \displaystyle S_{c^{\prime }}^{\prime } & := & \displaystyle (2m_{c})^{-1}\cdot S_{c}\cup \{(2m_{c})^{-1}\unicode[STIX]{x1D709}_{c}\},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime } & := & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-6C_{4}})\unicode[STIX]{x1D70C}_{c},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{c^{\prime }}^{\prime } & := & \displaystyle a,\nonumber\\ \displaystyle S_{c^{\prime }}^{\prime } & := & \displaystyle (2m_{c})^{-1}\cdot S_{c}\cup \{(2m_{c})^{-1}\unicode[STIX]{x1D709}_{c}\},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime } & := & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-6C_{4}})\unicode[STIX]{x1D70C}_{c},\nonumber\end{eqnarray}$$
thus the shifted Bohr set
 $n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime })$
will be a small subset of
$n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime })$
will be a small subset of
 $n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})$
in which the radius
$n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})$
in which the radius
![]() $\unicode[STIX]{x1D70C}_{c}$
has been reduced and an additional frequency
$\unicode[STIX]{x1D70C}_{c}$
has been reduced and an additional frequency
![]() $\unicode[STIX]{x1D709}_{c}/2m_{c}$
has been added. As we shall see, this particular choice of this linear data will allow us to utilize the approximate constraint (7.3).
$\unicode[STIX]{x1D709}_{c}/2m_{c}$
has been added. As we shall see, this particular choice of this linear data will allow us to utilize the approximate constraint (7.3).
The constraint (7.3) has the effect of approximately restricting
![]() $\unicode[STIX]{x1D6EF}_{c}$
(on a suitable Bohr set) to a coset of the orthogonal complement
$\unicode[STIX]{x1D6EF}_{c}$
(on a suitable Bohr set) to a coset of the orthogonal complement
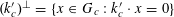 $(k_{c}^{\prime })^{\bot }=\{x\in G_{c}:k_{c}^{\prime }\cdot x=0\}$
of
$(k_{c}^{\prime })^{\bot }=\{x\in G_{c}:k_{c}^{\prime }\cdot x=0\}$
of
![]() $k_{c}^{\prime }$
in
$k_{c}^{\prime }$
in
![]() $G_{c}$
. Applying Theorem 5.1, (6.4), and the crucial bound (7.2), we may find a dilated torus
$G_{c}$
. Applying Theorem 5.1, (6.4), and the crucial bound (7.2), we may find a dilated torus
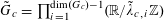 $\tilde{G}_{c}=\prod _{i=1}^{\dim (G_{c})-1}(\mathbb{R}/\tilde{\unicode[STIX]{x1D706}}_{c,i}\mathbb{Z})$
with volume
$\tilde{G}_{c}=\prod _{i=1}^{\dim (G_{c})-1}(\mathbb{R}/\tilde{\unicode[STIX]{x1D706}}_{c,i}\mathbb{Z})$
with volume
 $$\begin{eqnarray}\operatorname{vol}(\tilde{G}_{c})\ll \exp (\unicode[STIX]{x1D702}^{-4C_{2}})\operatorname{vol}(G_{c})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}(\tilde{G}_{c})\ll \exp (\unicode[STIX]{x1D702}^{-4C_{2}})\operatorname{vol}(G_{c})\end{eqnarray}$$
as well as a Lie group isomorphism
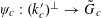 $\unicode[STIX]{x1D713}_{c}:(k_{c}^{\prime })^{\bot }\rightarrow \tilde{G}_{c}$
obeying the bilipschitz bounds
$\unicode[STIX]{x1D713}_{c}:(k_{c}^{\prime })^{\bot }\rightarrow \tilde{G}_{c}$
obeying the bilipschitz bounds
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}\Vert _{\operatorname{Lip}},\Vert \unicode[STIX]{x1D713}^{-1}\!\Vert _{\operatorname{ Lip}}\leqslant \exp (\unicode[STIX]{x1D702}^{-4C_{2}}).\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D713}\Vert _{\operatorname{Lip}},\Vert \unicode[STIX]{x1D713}^{-1}\!\Vert _{\operatorname{ Lip}}\leqslant \exp (\unicode[STIX]{x1D702}^{-4C_{2}}).\end{eqnarray}$$
In particular, if we define the even more dilated torus
 $$\begin{eqnarray}G_{c}^{\prime }:=\mathop{\prod }_{i=1}^{\dim (G_{c})-1}(\mathbb{R}/\text{exp}(\unicode[STIX]{x1D702}^{-4C_{2}})\tilde{\unicode[STIX]{x1D706}}_{c,i}\mathbb{Z})\end{eqnarray}$$
$$\begin{eqnarray}G_{c}^{\prime }:=\mathop{\prod }_{i=1}^{\dim (G_{c})-1}(\mathbb{R}/\text{exp}(\unicode[STIX]{x1D702}^{-4C_{2}})\tilde{\unicode[STIX]{x1D706}}_{c,i}\mathbb{Z})\end{eqnarray}$$
and let
 $\unicode[STIX]{x1D6FF}_{c}:G_{c}^{\prime }\rightarrow \tilde{G}_{c}$
be the rescaling map
$\unicode[STIX]{x1D6FF}_{c}:G_{c}^{\prime }\rightarrow \tilde{G}_{c}$
be the rescaling map
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{c}:(x_{i})_{i=1}^{\dim (G_{c})-1}\mapsto (\exp (-\unicode[STIX]{x1D702}^{-4C_{2}})x_{i})_{i=1}^{\dim (G_{c})-1}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{c}:(x_{i})_{i=1}^{\dim (G_{c})-1}\mapsto (\exp (-\unicode[STIX]{x1D702}^{-4C_{2}})x_{i})_{i=1}^{\dim (G_{c})-1}\end{eqnarray}$$
then we see that
 $\unicode[STIX]{x1D713}^{-1}\circ \unicode[STIX]{x1D6FF}_{c}:G_{c}^{\prime }\rightarrow (k_{c}^{\prime })^{\bot }$
is a
$\unicode[STIX]{x1D713}^{-1}\circ \unicode[STIX]{x1D6FF}_{c}:G_{c}^{\prime }\rightarrow (k_{c}^{\prime })^{\bot }$
is a
![]() $1$
-Lipschitz Lie group isomorphism.
$1$
-Lipschitz Lie group isomorphism.
An element of
 $n_{c^{\prime }}^{\prime }+B(S_{c}^{\prime },\unicode[STIX]{x1D70C}_{c}^{\prime })$
can be uniquely represented in the form
$n_{c^{\prime }}^{\prime }+B(S_{c}^{\prime },\unicode[STIX]{x1D70C}_{c}^{\prime })$
can be uniquely represented in the form
 $n_{c^{\prime }}^{\prime }+2m_{c}h$
for
$n_{c^{\prime }}^{\prime }+2m_{c}h$
for
 $h\in B(S_{c}\cup \{\unicode[STIX]{x1D709}_{c}\},\exp (-\unicode[STIX]{x1D702}^{-6C_{4}})\unicode[STIX]{x1D70C}_{c})$
. From (7.3), we know that the point
$h\in B(S_{c}\cup \{\unicode[STIX]{x1D709}_{c}\},\exp (-\unicode[STIX]{x1D702}^{-6C_{4}})\unicode[STIX]{x1D70C}_{c})$
. From (7.3), we know that the point
 $\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }+2m_{c}h)-\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime })$
lies within a
$\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }+2m_{c}h)-\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime })$
lies within a
 $O(\exp (-\unicode[STIX]{x1D702}^{-3C_{4}}))$
-neighbourhood of the subtorus
$O(\exp (-\unicode[STIX]{x1D702}^{-3C_{4}}))$
-neighbourhood of the subtorus
![]() $(k_{c}^{\prime })^{\bot }$
. Using the lower bound in (7.2), we can find a locally linear projection
$(k_{c}^{\prime })^{\bot }$
. Using the lower bound in (7.2), we can find a locally linear projection
![]() $\unicode[STIX]{x1D70B}_{c}$
from this neighbourhood to the subtorus itself (e.g. by viewing the subtorus locally as a graph in
$\unicode[STIX]{x1D70B}_{c}$
from this neighbourhood to the subtorus itself (e.g. by viewing the subtorus locally as a graph in
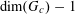 $\dim (G_{c})-1$
of the
$\dim (G_{c})-1$
of the
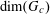 $\dim (G_{c})$
coordinates and then projecting in the direction of the remaining coordinate), which moves each point in the neighbourhood by at most
$\dim (G_{c})$
coordinates and then projecting in the direction of the remaining coordinate), which moves each point in the neighbourhood by at most
 $O(\exp (-\unicode[STIX]{x1D702}^{-2C_{4}}))$
. From the
$O(\exp (-\unicode[STIX]{x1D702}^{-2C_{4}}))$
. From the
![]() $1$
-Lipschitz nature of
$1$
-Lipschitz nature of
![]() $F_{c}$
, we thus have
$F_{c}$
, we thus have
 $$\begin{eqnarray}\displaystyle & & \displaystyle F_{c}(\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }+2m_{c}h))\nonumber\\ \displaystyle & & \displaystyle \quad =F_{c}(\unicode[STIX]{x1D70B}_{c}(\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }+2m_{c}h)-\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }))+\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }))+O(\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F_{c}(\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }+2m_{c}h))\nonumber\\ \displaystyle & & \displaystyle \quad =F_{c}(\unicode[STIX]{x1D70B}_{c}(\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }+2m_{c}h)-\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }))+\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }))+O(\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})).\nonumber\end{eqnarray}$$
We can rewrite this as
 $$\begin{eqnarray}F_{c}(\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }+2m_{c}h))=F_{c^{\prime }}^{\prime }(\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }(n_{c^{\prime }}^{\prime }+2m_{c}h))+O(\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})),\end{eqnarray}$$
$$\begin{eqnarray}F_{c}(\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }+2m_{c}h))=F_{c^{\prime }}^{\prime }(\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }(n_{c^{\prime }}^{\prime }+2m_{c}h))+O(\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})),\end{eqnarray}$$
where
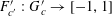 $F_{c^{\prime }}^{\prime }:G_{c}^{\prime }\rightarrow [-1,1]$
is the
$F_{c^{\prime }}^{\prime }:G_{c}^{\prime }\rightarrow [-1,1]$
is the
![]() $1$
-Lipschitz function
$1$
-Lipschitz function
 $$\begin{eqnarray}F_{c^{\prime }}^{\prime }(x):=F_{c}(\unicode[STIX]{x1D713}_{c}^{-1}(\unicode[STIX]{x1D6FF}_{c}(x)))+\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}F_{c^{\prime }}^{\prime }(x):=F_{c}(\unicode[STIX]{x1D713}_{c}^{-1}(\unicode[STIX]{x1D6FF}_{c}(x)))+\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime })\end{eqnarray}$$
and
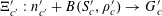 $\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }:n_{c^{\prime }}^{\prime }+B(S_{c}^{\prime },\unicode[STIX]{x1D70C}_{c}^{\prime })\rightarrow G_{c}^{\prime }$
takes the form
$\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }:n_{c^{\prime }}^{\prime }+B(S_{c}^{\prime },\unicode[STIX]{x1D70C}_{c}^{\prime })\rightarrow G_{c}^{\prime }$
takes the form
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }(n_{c^{\prime }}^{\prime }+2mch):=\unicode[STIX]{x1D6FF}_{c}^{-1}(\unicode[STIX]{x1D713}_{c}(\unicode[STIX]{x1D70B}_{c}(\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }+2m_{c}h)-\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }))+\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }))).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }(n_{c^{\prime }}^{\prime }+2mch):=\unicode[STIX]{x1D6FF}_{c}^{-1}(\unicode[STIX]{x1D713}_{c}(\unicode[STIX]{x1D70B}_{c}(\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }+2m_{c}h)-\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }))+\unicode[STIX]{x1D6EF}_{c}(n_{c^{\prime }}^{\prime }))).\end{eqnarray}$$
The map
![]() $\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }$
is the composition of a locally quadratic map with three locally linear maps, and is hence also locally quadratic. This concludes the construction of all the required quadratic data
$\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }$
is the composition of a locally quadratic map with three locally linear maps, and is hence also locally quadratic. This concludes the construction of all the required quadratic data
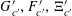 $G_{c^{\prime }}^{\prime },F_{c^{\prime }}^{\prime },\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }$
when
$G_{c^{\prime }}^{\prime },F_{c^{\prime }}^{\prime },\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }$
when
![]() $c^{\prime }$
arises from a poorly distributed
$c^{\prime }$
arises from a poorly distributed
![]() $c$
.
$c$
.
It remains to verify the claims (6.17)–(6.23) of Theorem 6.7. The claim (6.17) is clear; in fact, the frequency sets
![]() $S_{c^{\prime }}^{\prime }$
are either equal to their original counterparts
$S_{c^{\prime }}^{\prime }$
are either equal to their original counterparts
![]() $S_{c}$
or have the addition of just one further frequency
$S_{c}$
or have the addition of just one further frequency
![]() $\unicode[STIX]{x1D709}_{c}$
, so we even obtain the improved bound
$\unicode[STIX]{x1D709}_{c}$
, so we even obtain the improved bound
 $d(v^{\prime })\leqslant d(v)+1$
in our construction here. Since the dilated torus
$d(v^{\prime })\leqslant d(v)+1$
in our construction here. Since the dilated torus
![]() $G_{c^{\prime }}^{\prime }$
is either equal to
$G_{c^{\prime }}^{\prime }$
is either equal to
![]() $G_{c}$
when
$G_{c}$
when
![]() $c$
is not poorly distributed, or has one lower dimension than
$c$
is not poorly distributed, or has one lower dimension than
![]() $G_{c}$
if
$G_{c}$
if
![]() $c$
is poorly distributed, we obtain the bounds (6.18), (6.19). Since
$c$
is poorly distributed, we obtain the bounds (6.18), (6.19). Since
![]() $\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }$
is either equal to
$\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }$
is either equal to
![]() $\unicode[STIX]{x1D70C}_{c}$
when
$\unicode[STIX]{x1D70C}_{c}$
when
![]() $c$
is not poorly distributed, or
$c$
is not poorly distributed, or
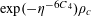 $\exp (-\unicode[STIX]{x1D702}^{-6C_{4}})\unicode[STIX]{x1D70C}_{c}$
when
$\exp (-\unicode[STIX]{x1D702}^{-6C_{4}})\unicode[STIX]{x1D70C}_{c}$
when
![]() $c$
is poorly distributed, we obtain (6.20) (with a little room to spare). As for the volume bound,
$c$
is poorly distributed, we obtain (6.20) (with a little room to spare). As for the volume bound,
![]() $G_{c^{\prime }}^{\prime }$
clearly has the same volume as
$G_{c^{\prime }}^{\prime }$
clearly has the same volume as
![]() $G_{c}$
when
$G_{c}$
when
![]() $c$
is not poorly distributed, and when
$c$
is not poorly distributed, and when
![]() $c$
is poorly distributed we have
$c$
is poorly distributed we have
 $$\begin{eqnarray}\operatorname{vol}(G_{c^{\prime }}^{\prime })=\exp (-\unicode[STIX]{x1D702}^{-4C_{2}}\dim (\tilde{G}_{c^{\prime }}))\operatorname{vol}(\tilde{G}_{c^{\prime }})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}(G_{c^{\prime }}^{\prime })=\exp (-\unicode[STIX]{x1D702}^{-4C_{2}}\dim (\tilde{G}_{c^{\prime }}))\operatorname{vol}(\tilde{G}_{c^{\prime }})\end{eqnarray}$$
which by (7.13), (6.3) is bounded in turn by
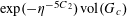 $\exp (-\unicode[STIX]{x1D702}^{-5C_{2}})\operatorname{vol}(G_{c})$
, which yields (6.21), again with a little bit of room to spare (because the bounds here only increased the volume by factors that involved
$\exp (-\unicode[STIX]{x1D702}^{-5C_{2}})\operatorname{vol}(G_{c})$
, which yields (6.21), again with a little bit of room to spare (because the bounds here only increased the volume by factors that involved
![]() $C_{2}$
rather than
$C_{2}$
rather than
![]() $C_{3}$
).
$C_{3}$
).
Now we establish (6.22). From the triangle inequality we have
 $$\begin{eqnarray}\displaystyle |\text{waste}(v^{\prime })-\operatorname{waste}(v)| & {\leqslant} & \displaystyle |\mathbb{E}f(\mathbf{a}_{v^{\prime }})-\mathbb{E}f(\mathbf{a}_{v})|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{c\in C}\mathbb{P}(\mathbf{c}=c)|\mathbb{E}(f(\mathbf{a}_{v^{\prime }})|\mathbf{c}=c)-\mathbb{E}(f(\mathbf{a}_{v})|\mathbf{c}=c)|\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\text{waste}(v^{\prime })-\operatorname{waste}(v)| & {\leqslant} & \displaystyle |\mathbb{E}f(\mathbf{a}_{v^{\prime }})-\mathbb{E}f(\mathbf{a}_{v})|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{c\in C}\mathbb{P}(\mathbf{c}=c)|\mathbb{E}(f(\mathbf{a}_{v^{\prime }})|\mathbf{c}=c)-\mathbb{E}(f(\mathbf{a}_{v})|\mathbf{c}=c)|\nonumber\end{eqnarray}$$
so it will suffice to show that
 $$\begin{eqnarray}|\mathbb{E}(f(\mathbf{a}_{v^{\prime }})|\mathbf{c}=c)-\mathbb{E}(f(\mathbf{a}_{v})|\mathbf{c}=c)|\leqslant \unicode[STIX]{x1D702}^{C_{3}}\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(f(\mathbf{a}_{v^{\prime }})|\mathbf{c}=c)-\mathbb{E}(f(\mathbf{a}_{v})|\mathbf{c}=c)|\leqslant \unicode[STIX]{x1D702}^{C_{3}}\end{eqnarray}$$
for each
![]() $c$
in the essential range of
$c$
in the essential range of
![]() $\mathbf{c}$
.
$\mathbf{c}$
.
The claim is trivial when
![]() $c$
is not poorly distributed, since in this case
$c$
is not poorly distributed, since in this case
![]() $\mathbf{a}_{v}$
and
$\mathbf{a}_{v}$
and
![]() $\mathbf{a}_{v^{\prime }}$
have identical distribution after conditioning to
$\mathbf{a}_{v^{\prime }}$
have identical distribution after conditioning to
![]() $\mathbf{c}=c$
. If
$\mathbf{c}=c$
. If
![]() $c$
is poorly distributed, then (after conditioning to
$c$
is poorly distributed, then (after conditioning to
![]() $\mathbf{c}=c$
)
$\mathbf{c}=c$
)
![]() $\mathbf{a}_{v}$
is drawn regularly from
$\mathbf{a}_{v}$
is drawn regularly from
 $n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
, while
$n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
, while
![]() $\mathbf{a}_{v^{\prime }}$
has the distribution of
$\mathbf{a}_{v^{\prime }}$
has the distribution of
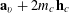 $\mathbf{a}_{v}+2m_{c}\mathbf{h}_{c}$
where
$\mathbf{a}_{v}+2m_{c}\mathbf{h}_{c}$
where
![]() $\mathbf{h}_{c}$
is drawn regularly from
$\mathbf{h}_{c}$
is drawn regularly from
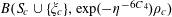 $B(S_{c}\cup \{\unicode[STIX]{x1D709}_{c}\},\exp (-\unicode[STIX]{x1D702}^{-6C_{4}})\unicode[STIX]{x1D70C}_{c})$
independently of
$B(S_{c}\cup \{\unicode[STIX]{x1D709}_{c}\},\exp (-\unicode[STIX]{x1D702}^{-6C_{4}})\unicode[STIX]{x1D70C}_{c})$
independently of
![]() $\mathbf{a}_{v}$
(after conditioning to
$\mathbf{a}_{v}$
(after conditioning to
![]() $\mathbf{c}=c$
). The required bound (6.22) now follows from Lemma 4.4 (and (6.3)).
$\mathbf{c}=c$
). The required bound (6.22) now follows from Lemma 4.4 (and (6.3)).
Finally, we prove (6.23). Our task is to show that
 $$\begin{eqnarray}\mathbb{E}|f(\mathbf{a}_{v^{\prime }})-\mathbf{f}_{v^{\prime }}(\mathbf{a}_{v^{\prime }})|^{2}\leqslant \mathbb{E}|f(\mathbf{a}_{v})-\mathbf{f}_{v}(\mathbf{a}_{v})|^{2}+\unicode[STIX]{x1D702}^{3C_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}|f(\mathbf{a}_{v^{\prime }})-\mathbf{f}_{v^{\prime }}(\mathbf{a}_{v^{\prime }})|^{2}\leqslant \mathbb{E}|f(\mathbf{a}_{v})-\mathbf{f}_{v}(\mathbf{a}_{v})|^{2}+\unicode[STIX]{x1D702}^{3C_{2}}.\end{eqnarray}$$
By the triangle inequality as before, it suffices to show that
 $$\begin{eqnarray}\mathbb{E}(|f(\mathbf{a}_{v^{\prime }})-\mathbf{f}_{v^{\prime }}(\mathbf{a}_{v^{\prime }})|^{2}|\mathbf{c}=c)\leqslant \mathbb{E}(|f(\mathbf{a}_{v})-\mathbf{f}_{v}(\mathbf{a}_{v})|^{2}|\mathbf{c}=c)+\unicode[STIX]{x1D702}^{3C_{2}}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}(|f(\mathbf{a}_{v^{\prime }})-\mathbf{f}_{v^{\prime }}(\mathbf{a}_{v^{\prime }})|^{2}|\mathbf{c}=c)\leqslant \mathbb{E}(|f(\mathbf{a}_{v})-\mathbf{f}_{v}(\mathbf{a}_{v})|^{2}|\mathbf{c}=c)+\unicode[STIX]{x1D702}^{3C_{2}}\end{eqnarray}$$
for all
![]() $c$
in the essential range of
$c$
in the essential range of
![]() $\mathbf{c}$
. This is trivial for
$\mathbf{c}$
. This is trivial for
![]() $c$
not poorly distributed, so assume
$c$
not poorly distributed, so assume
![]() $c$
is poorly distributed. From (7.14) we then have
$c$
is poorly distributed. From (7.14) we then have
 $$\begin{eqnarray}\mathbf{f}_{v^{\prime }}(\mathbf{a}_{v^{\prime }})=\mathbf{f}_{v}(\mathbf{a}_{v^{\prime }})+O(\exp (-\unicode[STIX]{x1D702}^{-2C_{4}}))\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{f}_{v^{\prime }}(\mathbf{a}_{v^{\prime }})=\mathbf{f}_{v}(\mathbf{a}_{v^{\prime }})+O(\exp (-\unicode[STIX]{x1D702}^{-2C_{4}}))\end{eqnarray}$$
and also
 $$\begin{eqnarray}\mathbf{f}_{v}(a)=F_{c}(\unicode[STIX]{x1D6EF}_{c}(a))\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{f}_{v}(a)=F_{c}(\unicode[STIX]{x1D6EF}_{c}(a))\end{eqnarray}$$
for
 $a\in B(S_{c},\unicode[STIX]{x1D70C}_{c})$
, so by the triangle inequality it suffices to show that
$a\in B(S_{c},\unicode[STIX]{x1D70C}_{c})$
, so by the triangle inequality it suffices to show that
 $$\begin{eqnarray}\mathbb{E}(|f(\mathbf{a}_{v^{\prime }})-F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}_{v^{\prime }}))|^{2}|\mathbf{c}=c)\leqslant \mathbb{E}(|f(\mathbf{a}_{v})-F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}_{v}))|^{2}|\mathbf{c}=c)+\unicode[STIX]{x1D702}^{4C_{2}}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}(|f(\mathbf{a}_{v^{\prime }})-F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}_{v^{\prime }}))|^{2}|\mathbf{c}=c)\leqslant \mathbb{E}(|f(\mathbf{a}_{v})-F_{c}(\unicode[STIX]{x1D6EF}_{c}(\mathbf{a}_{v}))|^{2}|\mathbf{c}=c)+\unicode[STIX]{x1D702}^{4C_{2}}\end{eqnarray}$$
(for example). But this follows by repeating the proof of (7.15), with the function
![]() $f$
replaced by
$f$
replaced by
 $|f-F_{c}\circ \unicode[STIX]{x1D6EF}_{c}|^{2}$
. This completes the proof of Theorem 6.7.
$|f-F_{c}\circ \unicode[STIX]{x1D6EF}_{c}|^{2}$
. This completes the proof of Theorem 6.7.
8 Bad approximation implies energy decrement
The remaining task in the paper is to prove Theorem 6.6. In this section we will establish this result contingent on a local inverse Gowers norm theorem (Theorem 8.1) that will be proven in later sections. We begin by stating the (rather technical) precise form of that theorem that we will need.
Theorem 8.1 (Local inverse
 $U^{3}$
theorem).
$U^{3}$
theorem).
Let
![]() $p$
be a prime, and let
$p$
be a prime, and let
![]() $S$
be a subset of
$S$
be a subset of
![]() $\mathbb{Z}/p\mathbb{Z}$
containing at least one non-zero element. Let
$\mathbb{Z}/p\mathbb{Z}$
containing at least one non-zero element. Let
![]() $\unicode[STIX]{x1D702}$
be a real parameter with
$\unicode[STIX]{x1D702}$
be a real parameter with
 $0<\unicode[STIX]{x1D702}<{\textstyle \frac{1}{2}}$
. Let
$0<\unicode[STIX]{x1D702}<{\textstyle \frac{1}{2}}$
. Let
![]() $K$
be the quantity
$K$
be the quantity
 $$\begin{eqnarray}K:=\frac{1}{\unicode[STIX]{x1D702}}+|S|,\end{eqnarray}$$
$$\begin{eqnarray}K:=\frac{1}{\unicode[STIX]{x1D702}}+|S|,\end{eqnarray}$$
and let
 $\unicode[STIX]{x1D70C}_{0},\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2},\ldots ,\unicode[STIX]{x1D70C}_{10}$
be real numbers satisfying
$\unicode[STIX]{x1D70C}_{0},\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2},\ldots ,\unicode[STIX]{x1D70C}_{10}$
be real numbers satisfying
 $$\begin{eqnarray}0<\unicode[STIX]{x1D70C}_{10}<\cdots <\unicode[STIX]{x1D70C}_{0}<1/2\end{eqnarray}$$
$$\begin{eqnarray}0<\unicode[STIX]{x1D70C}_{10}<\cdots <\unicode[STIX]{x1D70C}_{0}<1/2\end{eqnarray}$$
as well as the separation condition
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{i+1}\geqslant \exp (K^{C_{2}})\unicode[STIX]{x1D70C}_{i}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{i+1}\geqslant \exp (K^{C_{2}})\unicode[STIX]{x1D70C}_{i}\end{eqnarray}$$
for all
 $i=0,\ldots ,9$
. Assume that the prime
$i=0,\ldots ,9$
. Assume that the prime
![]() $p$
is huge relative to the reciprocal of these parameters, in the sense that
$p$
is huge relative to the reciprocal of these parameters, in the sense that
 $$\begin{eqnarray}p\geqslant \unicode[STIX]{x1D70C}_{10}^{-K^{C_{2}^{3}}}.\end{eqnarray}$$
$$\begin{eqnarray}p\geqslant \unicode[STIX]{x1D70C}_{10}^{-K^{C_{2}^{3}}}.\end{eqnarray}$$
Let
 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
be a
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
be a
![]() $1$
-bounded function such that
$1$
-bounded function such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}f(\mathbf{h}_{0}+\mathbf{h}_{1}+\mathbf{h}_{2})\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime }+\mathbf{h}_{2})\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}+\mathbf{h}_{2})f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime }+\mathbf{h}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}+\mathbf{h}_{2}^{\prime })f(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime }+\mathbf{h}_{2}^{\prime })f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}+\mathbf{h}_{2}^{\prime })\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime }+\mathbf{h}_{2}^{\prime })|\nonumber\\ \displaystyle & & \displaystyle \qquad \geqslant \unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}f(\mathbf{h}_{0}+\mathbf{h}_{1}+\mathbf{h}_{2})\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime }+\mathbf{h}_{2})\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}+\mathbf{h}_{2})f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime }+\mathbf{h}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(\mathbf{h}_{0}+\mathbf{h}_{1}+\mathbf{h}_{2}^{\prime })f(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime }+\mathbf{h}_{2}^{\prime })f(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}+\mathbf{h}_{2}^{\prime })\overline{f}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime }+\mathbf{h}_{2}^{\prime })|\nonumber\\ \displaystyle & & \displaystyle \qquad \geqslant \unicode[STIX]{x1D702}\end{eqnarray}$$
whenever
 $\mathbf{h}_{0},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1},\mathbf{h}_{1}^{\prime },\mathbf{h}_{2},\mathbf{h}_{2}^{\prime }$
are drawn independently and regularly from
$\mathbf{h}_{0},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1},\mathbf{h}_{1}^{\prime },\mathbf{h}_{2},\mathbf{h}_{2}^{\prime }$
are drawn independently and regularly from
 $B(S,\unicode[STIX]{x1D70C}_{0})$
,
$B(S,\unicode[STIX]{x1D70C}_{0})$
,
 $B(S,\unicode[STIX]{x1D70C}_{0})$
,
$B(S,\unicode[STIX]{x1D70C}_{0})$
,
 $B(S,\unicode[STIX]{x1D70C}_{1})$
,
$B(S,\unicode[STIX]{x1D70C}_{1})$
,
 $B(S,\unicode[STIX]{x1D70C}_{1})$
,
$B(S,\unicode[STIX]{x1D70C}_{1})$
,
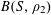 $B(S,\unicode[STIX]{x1D70C}_{2})$
, and
$B(S,\unicode[STIX]{x1D70C}_{2})$
, and
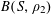 $B(S,\unicode[STIX]{x1D70C}_{2})$
respectively. Then there exists a positive integer
$B(S,\unicode[STIX]{x1D70C}_{2})$
respectively. Then there exists a positive integer
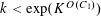 $k<\exp (K^{O(C_{1})})$
, a set
$k<\exp (K^{O(C_{1})})$
, a set
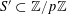 $S^{\prime }\subset \mathbb{Z}/p\mathbb{Z}$
,
$S^{\prime }\subset \mathbb{Z}/p\mathbb{Z}$
,
![]() $S^{\prime }\supset S$
, with
$S^{\prime }\supset S$
, with
 $$\begin{eqnarray}|S^{\prime }|\leqslant |S|+O(\unicode[STIX]{x1D702}^{-O(C_{1})}),\end{eqnarray}$$
$$\begin{eqnarray}|S^{\prime }|\leqslant |S|+O(\unicode[STIX]{x1D702}^{-O(C_{1})}),\end{eqnarray}$$
a locally quadratic phase
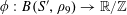 $\unicode[STIX]{x1D719}:B(S^{\prime },\unicode[STIX]{x1D70C}_{9})\rightarrow \mathbb{R}/\mathbb{Z}$
, and a function
$\unicode[STIX]{x1D719}:B(S^{\prime },\unicode[STIX]{x1D70C}_{9})\rightarrow \mathbb{R}/\mathbb{Z}$
, and a function
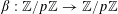 $\unicode[STIX]{x1D6FD}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D6FD}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\mathop{\sum }_{n\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}=n)\biggl|\mathbb{E}f(n+k\mathbf{m})e\biggl(-\unicode[STIX]{x1D719}(\mathbf{m})-\frac{\unicode[STIX]{x1D6FD}(n)\mathbf{m}}{p}\biggr)\biggr|\gg \unicode[STIX]{x1D702}^{O(C_{1})}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}=n)\biggl|\mathbb{E}f(n+k\mathbf{m})e\biggl(-\unicode[STIX]{x1D719}(\mathbf{m})-\frac{\unicode[STIX]{x1D6FD}(n)\mathbf{m}}{p}\biggr)\biggr|\gg \unicode[STIX]{x1D702}^{O(C_{1})}\end{eqnarray}$$
if
![]() $\mathbf{n},\mathbf{m}$
are drawn independently and regularly from
$\mathbf{n},\mathbf{m}$
are drawn independently and regularly from
 $B_{S}(0,\unicode[STIX]{x1D70C}_{0})$
and
$B_{S}(0,\unicode[STIX]{x1D70C}_{0})$
and
 $B_{S^{\prime }}(0,\unicode[STIX]{x1D70C}_{10})$
respectively.
$B_{S^{\prime }}(0,\unicode[STIX]{x1D70C}_{10})$
respectively.
Remarks.
The parameters
 $\unicode[STIX]{x1D70C}_{3},\ldots ,\unicode[STIX]{x1D70C}_{8}$
do not have any role in the statement of this result, but they appear in the proof. We have retained them to avoid a potentially confusing relabelling.
$\unicode[STIX]{x1D70C}_{3},\ldots ,\unicode[STIX]{x1D70C}_{8}$
do not have any role in the statement of this result, but they appear in the proof. We have retained them to avoid a potentially confusing relabelling.
Informally, this theorem asserts that if
![]() $f$
has a large
$f$
has a large
![]() $U^{3}$
norm on
$U^{3}$
norm on
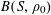 $B(S,\unicode[STIX]{x1D70C}_{0})$
, then
$B(S,\unicode[STIX]{x1D70C}_{0})$
, then
![]() $f$
will correlate with a locally quadratic phase
$f$
will correlate with a locally quadratic phase
 $n+km\mapsto \unicode[STIX]{x1D719}(m)+\unicode[STIX]{x1D6FD}(n)m/p$
on translates
$n+km\mapsto \unicode[STIX]{x1D719}(m)+\unicode[STIX]{x1D6FD}(n)m/p$
on translates
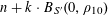 $n+k\cdot B_{S^{\prime }}(0,\unicode[STIX]{x1D70C}_{10})$
of
$n+k\cdot B_{S^{\prime }}(0,\unicode[STIX]{x1D70C}_{10})$
of
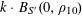 $k\cdot B_{S^{\prime }}(0,\unicode[STIX]{x1D70C}_{10})$
, with polynomial bounds on the correlation. Although we will not make crucial use of this fact in our arguments, it may be noted that the homogeneous component
$k\cdot B_{S^{\prime }}(0,\unicode[STIX]{x1D70C}_{10})$
, with polynomial bounds on the correlation. Although we will not make crucial use of this fact in our arguments, it may be noted that the homogeneous component
![]() $\unicode[STIX]{x1D719}$
of this locally quadratic phase does not depend on the translation parameter
$\unicode[STIX]{x1D719}$
of this locally quadratic phase does not depend on the translation parameter
![]() $n$
. In the bounded rank case
$n$
. In the bounded rank case
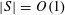 $|S|=O(1)$
, a theorem very roughly of this form was established in [Reference Green and Tao14]; the key point in Theorem 8.1 is that the inverse theory of [Reference Green and Tao14] can be localized to a Bohr set without having the lower bound
$|S|=O(1)$
, a theorem very roughly of this form was established in [Reference Green and Tao14]; the key point in Theorem 8.1 is that the inverse theory of [Reference Green and Tao14] can be localized to a Bohr set without having the lower bound
![]() $\unicode[STIX]{x1D702}^{O(C_{1})}$
on the correlation appearing in (8.6) depend on the rank
$\unicode[STIX]{x1D702}^{O(C_{1})}$
on the correlation appearing in (8.6) depend on the rank
![]() $|S|$
or radius
$|S|$
or radius
![]() $\unicode[STIX]{x1D70C}_{0}$
of the Bohr set (although these parameters certainly influence the range of the variables
$\unicode[STIX]{x1D70C}_{0}$
of the Bohr set (although these parameters certainly influence the range of the variables
![]() $\mathbf{n},\mathbf{m}$
appearing in (8.6)).
$\mathbf{n},\mathbf{m}$
appearing in (8.6)).
The proof of Theorem 8.1 will occupy most of the remainder of this paper. To a large extent, it may be understood separately of our main arguments, requiring little of the notation of §3, for example. In this section, we will assume Theorem 8.1 and use it to establish Theorem 6.6.
For the remainder of this section, the notation and hypotheses will be as in Theorem 6.6. Namely, we fix a prime
![]() $p$
, a function
$p$
, a function
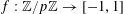 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
, and a parameter
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
, and a parameter
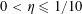 $0<\unicode[STIX]{x1D702}\leqslant 1/10$
, and assume (3.21). We also suppose that
$0<\unicode[STIX]{x1D702}\leqslant 1/10$
, and assume (3.21). We also suppose that
 $$\begin{eqnarray}v=(C,\mathbf{c},(n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}))_{c\in C},(G_{c})_{c\in C},(F_{c})_{c\in C},(\unicode[STIX]{x1D6EF}_{c})_{c\in C})\end{eqnarray}$$
$$\begin{eqnarray}v=(C,\mathbf{c},(n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c}))_{c\in C},(G_{c})_{c\in C},(F_{c})_{c\in C},(\unicode[STIX]{x1D6EF}_{c})_{c\in C})\end{eqnarray}$$
is a structured local approximant obeying (6.3)–(6.6), and one of (6.8) or (6.9) holds. Our objective is to construct a structured local approximant
 $$\begin{eqnarray}v^{\prime }=(C^{\prime },\mathbf{c}^{\prime },(n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }))_{c^{\prime }\in C^{\prime }},(G_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(F_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }})\end{eqnarray}$$
$$\begin{eqnarray}v^{\prime }=(C^{\prime },\mathbf{c}^{\prime },(n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }))_{c^{\prime }\in C^{\prime }},(G_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(F_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }})\end{eqnarray}$$
obeying the bounds (6.10)–(6.15). The situation here is a formalization of Example 8 from §3.
Let
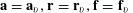 $\mathbf{a}=\mathbf{a}_{v},\mathbf{r}=\mathbf{r}_{v},\mathbf{f}=\mathbf{f}_{v}$
be the random variables associated to
$\mathbf{a}=\mathbf{a}_{v},\mathbf{r}=\mathbf{r}_{v},\mathbf{f}=\mathbf{f}_{v}$
be the random variables associated to
![]() $v$
in Definition 6.1. We can unify the hypotheses (6.8), (6.9) by introducing the quadrilinear form
$v$
in Definition 6.1. We can unify the hypotheses (6.8), (6.9) by introducing the quadrilinear form
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},\mathbf{f}_{3}):=\mathbb{E}\mathbf{f}_{0}(\mathbf{a})\mathbf{f}_{1}(\mathbf{a}+\mathbf{r})\mathbf{f}_{2}(\mathbf{a}+2\mathbf{r})\mathbf{f}_{3}(\mathbf{a}+3\mathbf{r}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},\mathbf{f}_{3}):=\mathbb{E}\mathbf{f}_{0}(\mathbf{a})\mathbf{f}_{1}(\mathbf{a}+\mathbf{r})\mathbf{f}_{2}(\mathbf{a}+2\mathbf{r})\mathbf{f}_{3}(\mathbf{a}+3\mathbf{r}),\end{eqnarray}$$
defined for arbitrary random (or deterministic) bounded functions
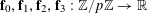 $\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},\mathbf{f}_{3}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{R}$
. From the definitions of
$\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},\mathbf{f}_{3}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{R}$
. From the definitions of
![]() $\operatorname{Err}_{1}$
and
$\operatorname{Err}_{1}$
and
![]() $\operatorname{Err}_{4}$
( just prior to (6.1)), the hypothesis (6.8) may be written as
$\operatorname{Err}_{4}$
( just prior to (6.1)), the hypothesis (6.8) may be written as
 $$\begin{eqnarray}|\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f,1,1,1)-\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f},1,1,1)|>\unicode[STIX]{x1D702},\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f,1,1,1)-\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f},1,1,1)|>\unicode[STIX]{x1D702},\end{eqnarray}$$
while (6.9) can be similarly written as
 $$\begin{eqnarray}|\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f,f,f,f)-\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f},\mathbf{f},\mathbf{f},\mathbf{f})|>\unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(f,f,f,f)-\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f},\mathbf{f},\mathbf{f},\mathbf{f})|>\unicode[STIX]{x1D702}.\end{eqnarray}$$
Applying the triangle inequality and the quadrilinearity of
![]() $\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}$
, we conclude that
$\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}$
, we conclude that
 $$\begin{eqnarray}|\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},\mathbf{f}_{3})|\gg \unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},\mathbf{f}_{3})|\gg \unicode[STIX]{x1D702}\end{eqnarray}$$
for some random functions
 $\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},\mathbf{f}_{3}$
, each of which is either equal to
$\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},\mathbf{f}_{3}$
, each of which is either equal to
![]() $1$
,
$1$
,
![]() $f$
, or
$f$
, or
![]() $f-\mathbf{f}$
, and with at least one of the functions
$f-\mathbf{f}$
, and with at least one of the functions
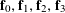 $\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},\mathbf{f}_{3}$
equal to
$\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},\mathbf{f}_{3}$
equal to
![]() $f-\mathbf{f}$
. For sake of concreteness we will assume that it is
$f-\mathbf{f}$
. For sake of concreteness we will assume that it is
![]() $\mathbf{f}_{3}$
that is equal to
$\mathbf{f}_{3}$
that is equal to
![]() $f-\mathbf{f}$
, thus
$f-\mathbf{f}$
, thus
 $$\begin{eqnarray}|\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},f-\mathbf{f})|\gg \unicode[STIX]{x1D702};\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6EC}_{\mathbf{a},\mathbf{r}}(\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2},f-\mathbf{f})|\gg \unicode[STIX]{x1D702};\end{eqnarray}$$
the other cases are treated similarly (with some changes to the numerical constants below) and are left to the interested reader.
We can write the left-hand side of (8.7) as
 $$\begin{eqnarray}\biggl|\mathop{\sum }_{c\in C}\mathbb{P}(\mathbf{c}=c)\mathbb{E}(\mathbf{f}_{0}(\mathbf{a})\mathbf{f}_{1}(\mathbf{a}+\mathbf{r})\mathbf{f}_{2}(\mathbf{a}+2\mathbf{r})(f-\mathbf{f})(\mathbf{a}+3\mathbf{r})|\mathbf{c}=c)\biggr|.\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathop{\sum }_{c\in C}\mathbb{P}(\mathbf{c}=c)\mathbb{E}(\mathbf{f}_{0}(\mathbf{a})\mathbf{f}_{1}(\mathbf{a}+\mathbf{r})\mathbf{f}_{2}(\mathbf{a}+2\mathbf{r})(f-\mathbf{f})(\mathbf{a}+3\mathbf{r})|\mathbf{c}=c)\biggr|.\end{eqnarray}$$
Applying Lemma 2.2, we conclude that with probability
![]() $\gg \unicode[STIX]{x1D702}$
, the variable
$\gg \unicode[STIX]{x1D702}$
, the variable
![]() $\mathbf{c}$
attains a value
$\mathbf{c}$
attains a value
![]() $c$
for which we have the lower bound
$c$
for which we have the lower bound
 $$\begin{eqnarray}|\mathbb{E}(\mathbf{f}_{0}(\mathbf{a})\mathbf{f}_{1}(\mathbf{a}+\mathbf{r})\mathbf{f}_{2}(\mathbf{a}+2\mathbf{r})(f-\mathbf{f})(\mathbf{a}+3\mathbf{r})|\mathbf{c}=c)|\gg \unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(\mathbf{f}_{0}(\mathbf{a})\mathbf{f}_{1}(\mathbf{a}+\mathbf{r})\mathbf{f}_{2}(\mathbf{a}+2\mathbf{r})(f-\mathbf{f})(\mathbf{a}+3\mathbf{r})|\mathbf{c}=c)|\gg \unicode[STIX]{x1D702}.\end{eqnarray}$$
We now use a local version of the standard “generalized von Neumann theorem” argument (based on several applications of the Cauchy–Schwarz inequality) to obtain some local correlation of
![]() $f-f_{c}$
with a quadratic phase.
$f-f_{c}$
with a quadratic phase.
Proposition 8.2. Let the notation and hypotheses be as above. For each
![]() $(a,c)$
in the essential range of
$(a,c)$
in the essential range of
![]() $(\mathbf{a},\mathbf{c})$
, there exists a natural number
$(\mathbf{a},\mathbf{c})$
, there exists a natural number
![]() $k_{a,c}$
with
$k_{a,c}$
with
 $$\begin{eqnarray}1\leqslant k_{a,c}<\unicode[STIX]{x1D702}^{-C_{3}},\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant k_{a,c}<\unicode[STIX]{x1D702}^{-C_{3}},\end{eqnarray}$$
a set
 $\tilde{S}_{a,c}\subset \mathbb{Z}/p\mathbb{Z}$
with
$\tilde{S}_{a,c}\subset \mathbb{Z}/p\mathbb{Z}$
with
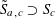 $\tilde{S}_{a,c}\supset S_{c}$
and
$\tilde{S}_{a,c}\supset S_{c}$
and
 $$\begin{eqnarray}|\tilde{S}_{a,c}|\leqslant |S_{c}|+\unicode[STIX]{x1D702}^{-C_{2}},\end{eqnarray}$$
$$\begin{eqnarray}|\tilde{S}_{a,c}|\leqslant |S_{c}|+\unicode[STIX]{x1D702}^{-C_{2}},\end{eqnarray}$$
and a locally quadratic function
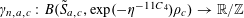 $\unicode[STIX]{x1D6FE}_{n,a,c}:B(\tilde{S}_{a,c},\exp (-\unicode[STIX]{x1D702}^{-11C_{4}})\unicode[STIX]{x1D70C}_{c})\rightarrow \mathbb{R}/\mathbb{Z}$
for each
$\unicode[STIX]{x1D6FE}_{n,a,c}:B(\tilde{S}_{a,c},\exp (-\unicode[STIX]{x1D702}^{-11C_{4}})\unicode[STIX]{x1D70C}_{c})\rightarrow \mathbb{R}/\mathbb{Z}$
for each
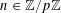 $n\in \mathbb{Z}/p\mathbb{Z}$
, such that
$n\in \mathbb{Z}/p\mathbb{Z}$
, such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Re}\,\mathop{\sum }_{a,c\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{a}=a,\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathbb{E}(\!(f-f_{c})(a+6\mathbf{n}+6k_{a,c}\mathbf{m})e(-\unicode[STIX]{x1D6FE}_{\mathbf{n},a,c}(\mathbf{m}))|\mathbf{a}=a,\mathbf{c}=c\!)\geqslant \unicode[STIX]{x1D702}^{C_{2}/10}\!,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Re}\,\mathop{\sum }_{a,c\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{a}=a,\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathbb{E}(\!(f-f_{c})(a+6\mathbf{n}+6k_{a,c}\mathbf{m})e(-\unicode[STIX]{x1D6FE}_{\mathbf{n},a,c}(\mathbf{m}))|\mathbf{a}=a,\mathbf{c}=c\!)\geqslant \unicode[STIX]{x1D702}^{C_{2}/10}\!,\end{eqnarray}$$
where, after conditioning to the event
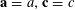 $\mathbf{a}=a,\mathbf{c}=c$
, the random variables
$\mathbf{a}=a,\mathbf{c}=c$
, the random variables
![]() $\mathbf{n}$
and
$\mathbf{n}$
and
![]() $\mathbf{m}$
are drawn regularly and independently from the Bohr sets
$\mathbf{m}$
are drawn regularly and independently from the Bohr sets
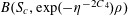 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C})$
and
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C})$
and
 $B(\tilde{S}_{a,c},\exp (-\unicode[STIX]{x1D702}^{-12C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively.
$B(\tilde{S}_{a,c},\exp (-\unicode[STIX]{x1D702}^{-12C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively.
Proof. Suppose for now that
![]() $c$
obeys (8.8). From Definition 6.1, once we condition to the event
$c$
obeys (8.8). From Definition 6.1, once we condition to the event
![]() $\mathbf{c}=c$
, the random variables
$\mathbf{c}=c$
, the random variables
![]() $\mathbf{a},\mathbf{r}$
are independent and regularly drawn from
$\mathbf{a},\mathbf{r}$
are independent and regularly drawn from
 $B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
and
$B(S_{c},\unicode[STIX]{x1D70C}_{c}/2)$
and
 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively; from (6.4) we have the bounds
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively; from (6.4) we have the bounds
 $$\begin{eqnarray}|S_{c}|\leqslant 8\unicode[STIX]{x1D702}^{-3C_{2}}\quad \text{and}\quad \unicode[STIX]{x1D70C}_{c}\geqslant \exp (-\unicode[STIX]{x1D702}^{-2C_{5}}).\end{eqnarray}$$
$$\begin{eqnarray}|S_{c}|\leqslant 8\unicode[STIX]{x1D702}^{-3C_{2}}\quad \text{and}\quad \unicode[STIX]{x1D70C}_{c}\geqslant \exp (-\unicode[STIX]{x1D702}^{-2C_{5}}).\end{eqnarray}$$
Also, the function
![]() $\mathbf{f}$
is now the deterministic function
$\mathbf{f}$
is now the deterministic function
 $$\begin{eqnarray}f_{c}(a):=F_{c}(\unicode[STIX]{x1D6EF}_{c}(a))\end{eqnarray}$$
$$\begin{eqnarray}f_{c}(a):=F_{c}(\unicode[STIX]{x1D6EF}_{c}(a))\end{eqnarray}$$
on the Bohr set
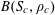 $B(S_{c},\unicode[STIX]{x1D70C}_{c})$
, and
$B(S_{c},\unicode[STIX]{x1D70C}_{c})$
, and
![]() $\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2}$
become deterministic functions
$\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2}$
become deterministic functions
![]() $f_{0,c}$
,
$f_{0,c}$
,
![]() $f_{1,c}$
and
$f_{1,c}$
and
![]() $f_{2,c}$
taking values in
$f_{2,c}$
taking values in
![]() $[-2,2]$
. Thus we have
$[-2,2]$
. Thus we have
 $$\begin{eqnarray}|\mathbb{E}(f_{0,c}(\mathbf{a})f_{1,c}(\mathbf{a}+\mathbf{r})f_{2,c}(\mathbf{a}+2\mathbf{r})f_{3,c}(\mathbf{a}+3\mathbf{r})|\mathbf{c}=c)|\gg \unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(f_{0,c}(\mathbf{a})f_{1,c}(\mathbf{a}+\mathbf{r})f_{2,c}(\mathbf{a}+2\mathbf{r})f_{3,c}(\mathbf{a}+3\mathbf{r})|\mathbf{c}=c)|\gg \unicode[STIX]{x1D702}\end{eqnarray}$$
where
 $f_{3,c}:=f-f_{c}$
.
$f_{3,c}:=f-f_{c}$
.
We now do a linear change of variable with conveniently chosen numerical coefficients that will facilitate a certain use of the Cauchy–Schwarz inequality to eliminate the bounded functions
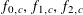 $f_{0,c},f_{1,c},f_{2,c}$
, leaving only the function
$f_{0,c},f_{1,c},f_{2,c}$
, leaving only the function
![]() $f_{3,c}$
. Continuing to condition on the event that
$f_{3,c}$
. Continuing to condition on the event that
![]() $\mathbf{c}=c$
, let
$\mathbf{c}=c$
, let
![]() $\mathbf{n}_{1},\mathbf{n}_{2}$
and
$\mathbf{n}_{1},\mathbf{n}_{2}$
and
![]() $\mathbf{n}_{3}$
be drawn regularly and independently from the Bohr sets
$\mathbf{n}_{3}$
be drawn regularly and independently from the Bohr sets
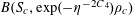 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C}_{c})$
,
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C}_{c})$
,
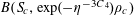 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-3C_{4}})\unicode[STIX]{x1D70C}_{c})$
, and
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-3C_{4}})\unicode[STIX]{x1D70C}_{c})$
, and
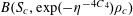 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively, independently of the previous random variables. We can use Lemma 4.4 (and (8.12)) to compare
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-4C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively, independently of the previous random variables. We can use Lemma 4.4 (and (8.12)) to compare
![]() $\mathbf{a}$
with
$\mathbf{a}$
with
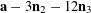 $\mathbf{a}-3\mathbf{n}_{2}-12\mathbf{n}_{3}$
, and conclude that
$\mathbf{a}-3\mathbf{n}_{2}-12\mathbf{n}_{3}$
, and conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c}(\mathbf{a}-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{1,c}(\mathbf{a}+\mathbf{r}-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{2,c}(\mathbf{a}+2\mathbf{r}-3\mathbf{n}_{2}-12\mathbf{n}_{3})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(\mathbf{a}+3\mathbf{r}-3\mathbf{n}_{2}-12\mathbf{n}_{3})|\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c}(\mathbf{a}-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{1,c}(\mathbf{a}+\mathbf{r}-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{2,c}(\mathbf{a}+2\mathbf{r}-3\mathbf{n}_{2}-12\mathbf{n}_{3})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(\mathbf{a}+3\mathbf{r}-3\mathbf{n}_{2}-12\mathbf{n}_{3})|\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
By another application of Lemma 4.4, we may compare
![]() $\mathbf{r}$
with
$\mathbf{r}$
with
 $\mathbf{r}+2\mathbf{n}_{1}+3\mathbf{n}_{2}+6\mathbf{n}_{3}$
, and conclude that
$\mathbf{r}+2\mathbf{n}_{1}+3\mathbf{n}_{2}+6\mathbf{n}_{3}$
, and conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c}(\mathbf{a}-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{1,c}(\mathbf{a}+\mathbf{r}+2\mathbf{n}_{1}-6\mathbf{n}_{3})f_{2,c}(\mathbf{a}+2\mathbf{r}+4\mathbf{n}_{1}+3\mathbf{n}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(\mathbf{a}+3\mathbf{r}+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c}(\mathbf{a}-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{1,c}(\mathbf{a}+\mathbf{r}+2\mathbf{n}_{1}-6\mathbf{n}_{3})f_{2,c}(\mathbf{a}+2\mathbf{r}+4\mathbf{n}_{1}+3\mathbf{n}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(\mathbf{a}+3\mathbf{r}+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
Finally, we use Lemma 4.4 to replace
![]() $\mathbf{a}$
by
$\mathbf{a}$
by
![]() $\mathbf{a}-3\mathbf{r}$
, so that
$\mathbf{a}-3\mathbf{r}$
, so that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c}(\mathbf{a}-3\mathbf{r}-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{1,c}(\mathbf{a}-2\mathbf{r}+2\mathbf{n}_{1}-6\mathbf{n}_{3})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{2,c}(\mathbf{a}-\mathbf{r}+4\mathbf{n}_{1}+3\mathbf{n}_{2})f_{3,c}(\mathbf{a}+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c}(\mathbf{a}-3\mathbf{r}-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{1,c}(\mathbf{a}-2\mathbf{r}+2\mathbf{n}_{1}-6\mathbf{n}_{3})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{2,c}(\mathbf{a}-\mathbf{r}+4\mathbf{n}_{1}+3\mathbf{n}_{2})f_{3,c}(\mathbf{a}+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
The purpose of this odd-seeming change of variables is that each of the functions
 $f_{0,c},f_{1,c},f_{2,c}$
now has an argument that involves only two of the three random variables
$f_{0,c},f_{1,c},f_{2,c}$
now has an argument that involves only two of the three random variables
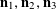 $\mathbf{n}_{1},\mathbf{n}_{2},\mathbf{n}_{3}$
, while the argument of the key function
$\mathbf{n}_{1},\mathbf{n}_{2},\mathbf{n}_{3}$
, while the argument of the key function
![]() $f_{3,c}$
depends on
$f_{3,c}$
depends on
 $\mathbf{n}_{1},\mathbf{n}_{2},\mathbf{n}_{3}$
only through their sum
$\mathbf{n}_{1},\mathbf{n}_{2},\mathbf{n}_{3}$
only through their sum
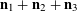 $\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}$
.
$\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}$
.
One can achieve a similar effect for the other three choices
![]() $\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2}$
for key function by suitable adjustment to the constants above; we leave the details to the interested reader.
$\mathbf{f}_{0},\mathbf{f}_{1},\mathbf{f}_{2}$
for key function by suitable adjustment to the constants above; we leave the details to the interested reader.
By Lemma 2.2, we see that with probability
![]() $\gg \unicode[STIX]{x1D702}$
(conditioning on
$\gg \unicode[STIX]{x1D702}$
(conditioning on
![]() $\mathbf{c}=c$
), the random variable
$\mathbf{c}=c$
), the random variable
![]() $\mathbf{a}$
attains a value
$\mathbf{a}$
attains a value
![]() $a$
such that
$a$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c}(a-3\mathbf{r}-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{1,c}(a-2\mathbf{r}+2\mathbf{n}_{1}-6\mathbf{n}_{3})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{2,c}(a-\mathbf{r}+4\mathbf{n}_{1}+3\mathbf{n}_{2})f_{3,c}(a+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{a}=a,\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c}(a-3\mathbf{r}-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{1,c}(a-2\mathbf{r}+2\mathbf{n}_{1}-6\mathbf{n}_{3})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{2,c}(a-\mathbf{r}+4\mathbf{n}_{1}+3\mathbf{n}_{2})f_{3,c}(a+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{a}=a,\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Let
![]() $a$
be such that (8.13) holds. We can then find an
$a$
be such that (8.13) holds. We can then find an
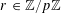 $r\in \mathbb{Z}/p\mathbb{Z}$
(depending on
$r\in \mathbb{Z}/p\mathbb{Z}$
(depending on
![]() $a,c$
) such that
$a,c$
) such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c}(a-3r-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{1,c}(a-2r+2\mathbf{n}_{1}-6\mathbf{n}_{3})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{2,c}(a-r+4\mathbf{n}_{1}+3\mathbf{n}_{2})f_{3,c}(a+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{a}=a,\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c}(a-3r-3\mathbf{n}_{2}-12\mathbf{n}_{3})f_{1,c}(a-2r+2\mathbf{n}_{1}-6\mathbf{n}_{3})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{2,c}(a-r+4\mathbf{n}_{1}+3\mathbf{n}_{2})f_{3,c}(a+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{a}=a,\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
We now suppress the additive structure on the first three arguments by rewriting the above bound as
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c,a}(\mathbf{n}_{2},\mathbf{n}_{3})f_{1,c,a}(\mathbf{n}_{1},\mathbf{n}_{3})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{2,c,a}(\mathbf{n}_{1},\mathbf{n}_{2})f_{3,c}(a\,+\,6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{0,c,a}(\mathbf{n}_{2},\mathbf{n}_{3})f_{1,c,a}(\mathbf{n}_{1},\mathbf{n}_{3})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{2,c,a}(\mathbf{n}_{1},\mathbf{n}_{2})f_{3,c}(a\,+\,6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702},\nonumber\end{eqnarray}$$
where
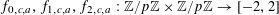 $f_{0,c,a},f_{1,c,a},f_{2,c,a}:\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}\rightarrow [-2,2]$
are bounded functions whose exact form
$f_{0,c,a},f_{1,c,a},f_{2,c,a}:\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}\rightarrow [-2,2]$
are bounded functions whose exact form
 $$\begin{eqnarray}\displaystyle f_{0,c,a}(n_{2},n_{3}) & := & \displaystyle f_{0,c}(a-3r-3n_{2}-12n_{3}),\nonumber\\ \displaystyle f_{1,c,a}(n_{1},n_{3}) & := & \displaystyle f_{1,c}(a-2r+2n_{1}-6n_{3}),\nonumber\\ \displaystyle f_{2,c,a}(n_{1},n_{2}) & := & \displaystyle f_{2,c}(a-r+4n_{1}+3n_{2})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{0,c,a}(n_{2},n_{3}) & := & \displaystyle f_{0,c}(a-3r-3n_{2}-12n_{3}),\nonumber\\ \displaystyle f_{1,c,a}(n_{1},n_{3}) & := & \displaystyle f_{1,c}(a-2r+2n_{1}-6n_{3}),\nonumber\\ \displaystyle f_{2,c,a}(n_{1},n_{2}) & := & \displaystyle f_{2,c}(a-r+4n_{1}+3n_{2})\nonumber\end{eqnarray}$$
will not be relevant in the arguments that follow.
We can eliminate the factor
![]() $f_{0,c,a}$
using Lemma 2.1 to conclude that
$f_{0,c,a}$
using Lemma 2.1 to conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{1,c,a}(\mathbf{n}_{1},\mathbf{n}_{3})f_{1,c,a}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{3})f_{2,c,a}(\mathbf{n}_{1},\mathbf{n}_{2})f_{2,c,a}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))f_{3,c}(a+6(\mathbf{n}_{1}^{\prime }+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{a}=a,\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}^{2}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{1,c,a}(\mathbf{n}_{1},\mathbf{n}_{3})f_{1,c,a}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{3})f_{2,c,a}(\mathbf{n}_{1},\mathbf{n}_{2})f_{2,c,a}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))f_{3,c}(a+6(\mathbf{n}_{1}^{\prime }+\mathbf{n}_{2}+\mathbf{n}_{3}))|\mathbf{a}=a,\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}^{2}\nonumber\end{eqnarray}$$
where
![]() $\mathbf{n}_{1}^{\prime }$
is an independent copy of
$\mathbf{n}_{1}^{\prime }$
is an independent copy of
![]() $\mathbf{n}_{1}$
(and also independent of
$\mathbf{n}_{1}$
(and also independent of
![]() $\mathbf{n}_{2},\mathbf{n}_{3}$
) on the event
$\mathbf{n}_{2},\mathbf{n}_{3}$
) on the event
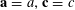 $\mathbf{a}=a,\mathbf{c}=c$
. We can similarly apply Lemma 2.1 to eliminate the
$\mathbf{a}=a,\mathbf{c}=c$
. We can similarly apply Lemma 2.1 to eliminate the
 $f_{1,c,a}(\mathbf{n}_{1},\mathbf{n}_{3})f_{1,c,a}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{3})$
variables to conclude that
$f_{1,c,a}(\mathbf{n}_{1},\mathbf{n}_{3})f_{1,c,a}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{3})$
variables to conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{2,c,a}(\mathbf{n}_{1},\mathbf{n}_{2})f_{2,c,a}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{2})f_{2,c,a}(\mathbf{n}_{1},\mathbf{n}_{2}^{\prime })f_{2,c,a}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{2}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))f_{3,c}(a+6(\mathbf{n}_{1}^{\prime }+\mathbf{n}_{2}+\mathbf{n}_{3}))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a+6(\mathbf{n}_{1}+\mathbf{n}_{2}^{\prime }+\mathbf{n}_{3}))f_{3,c}(a+6(\mathbf{n}_{1}^{\prime }+\mathbf{n}_{2}^{\prime }+\mathbf{n}_{3}))|\mathbf{a}=a,\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}^{4}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{2,c,a}(\mathbf{n}_{1},\mathbf{n}_{2})f_{2,c,a}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{2})f_{2,c,a}(\mathbf{n}_{1},\mathbf{n}_{2}^{\prime })f_{2,c,a}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{2}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a+6(\mathbf{n}_{1}+\mathbf{n}_{2}+\mathbf{n}_{3}))f_{3,c}(a+6(\mathbf{n}_{1}^{\prime }+\mathbf{n}_{2}+\mathbf{n}_{3}))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a+6(\mathbf{n}_{1}+\mathbf{n}_{2}^{\prime }+\mathbf{n}_{3}))f_{3,c}(a+6(\mathbf{n}_{1}^{\prime }+\mathbf{n}_{2}^{\prime }+\mathbf{n}_{3}))|\mathbf{a}=a,\mathbf{c}=c)\!|\gg \unicode[STIX]{x1D702}^{4}\nonumber\end{eqnarray}$$
and finally apply Lemma 2.1 to eliminate the
![]() $f_{2,c,a}$
terms and arrive at
$f_{2,c,a}$
terms and arrive at
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{3,c}(a\,+\,6(\mathbf{n}_{1}\,+\,\mathbf{n}_{2}\,+\,\mathbf{n}_{3}))f_{3,c}(a\,+\,6(\mathbf{n}_{1}^{\prime }\,+\,\mathbf{n}_{2}\,+\,\mathbf{n}_{3}))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a\,+\,6(\mathbf{n}_{1}\,+\,\mathbf{n}_{2}^{\prime }\,+\,\mathbf{n}_{3}))f_{3,c}(a\,+\,6(\mathbf{n}_{1}^{\prime }\,+\,\mathbf{n}_{2}^{\prime }\,+\,\mathbf{n}_{3}))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a\,+\,6(\mathbf{n}_{1}\,+\,\mathbf{n}_{2}\,+\,\mathbf{n}_{3}^{\prime }))f_{3,c}(a\,+\,6(\mathbf{n}_{1}^{\prime }\,+\,\mathbf{n}_{2}\,+\,\mathbf{n}_{3}^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a\,+\,6(\mathbf{n}_{1}\,+\,\mathbf{n}_{2}^{\prime }\,+\,\mathbf{n}_{3}^{\prime }))f_{3,c}(a\,+\,6(\mathbf{n}_{1}^{\prime }\,+\,\mathbf{n}_{2}^{\prime }\,+\,\mathbf{n}_{3}^{\prime }))|\mathbf{a}\,=\,a,\mathbf{c}\,=\,c)\!|\,\gg \,\unicode[STIX]{x1D702}^{8},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}\!(f_{3,c}(a\,+\,6(\mathbf{n}_{1}\,+\,\mathbf{n}_{2}\,+\,\mathbf{n}_{3}))f_{3,c}(a\,+\,6(\mathbf{n}_{1}^{\prime }\,+\,\mathbf{n}_{2}\,+\,\mathbf{n}_{3}))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a\,+\,6(\mathbf{n}_{1}\,+\,\mathbf{n}_{2}^{\prime }\,+\,\mathbf{n}_{3}))f_{3,c}(a\,+\,6(\mathbf{n}_{1}^{\prime }\,+\,\mathbf{n}_{2}^{\prime }\,+\,\mathbf{n}_{3}))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a\,+\,6(\mathbf{n}_{1}\,+\,\mathbf{n}_{2}\,+\,\mathbf{n}_{3}^{\prime }))f_{3,c}(a\,+\,6(\mathbf{n}_{1}^{\prime }\,+\,\mathbf{n}_{2}\,+\,\mathbf{n}_{3}^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{3,c}(a\,+\,6(\mathbf{n}_{1}\,+\,\mathbf{n}_{2}^{\prime }\,+\,\mathbf{n}_{3}^{\prime }))f_{3,c}(a\,+\,6(\mathbf{n}_{1}^{\prime }\,+\,\mathbf{n}_{2}^{\prime }\,+\,\mathbf{n}_{3}^{\prime }))|\mathbf{a}\,=\,a,\mathbf{c}\,=\,c)\!|\,\gg \,\unicode[STIX]{x1D702}^{8},\nonumber\end{eqnarray}$$
where
![]() $\mathbf{n}_{2}^{\prime },\mathbf{n}_{3}^{\prime }$
are independent copies of
$\mathbf{n}_{2}^{\prime },\mathbf{n}_{3}^{\prime }$
are independent copies of
![]() $\mathbf{n}_{2},\mathbf{n}_{3}$
respectively on
$\mathbf{n}_{2},\mathbf{n}_{3}$
respectively on
 $\mathbf{a}=a,\mathbf{c}=c$
, with
$\mathbf{a}=a,\mathbf{c}=c$
, with
 $\mathbf{n}_{1},\mathbf{n}_{2},\mathbf{n}_{3},\mathbf{n}_{1}^{\prime },\mathbf{n}_{2}^{\prime },\mathbf{n}_{3}^{\prime }$
all independent relative to
$\mathbf{n}_{1},\mathbf{n}_{2},\mathbf{n}_{3},\mathbf{n}_{1}^{\prime },\mathbf{n}_{2}^{\prime },\mathbf{n}_{3}^{\prime }$
all independent relative to
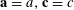 $\mathbf{a}=a,\mathbf{c}=c$
.
$\mathbf{a}=a,\mathbf{c}=c$
.
We now apply Theorem 8.1, replacing
![]() $\unicode[STIX]{x1D702}$
by a small multiple of
$\unicode[STIX]{x1D702}$
by a small multiple of
![]() $\unicode[STIX]{x1D702}^{8}$
, and choosing
$\unicode[STIX]{x1D702}^{8}$
, and choosing
 $\unicode[STIX]{x1D70C}_{i}:=\exp (-\unicode[STIX]{x1D702}^{-(\text{i}+2)C_{4}})\unicode[STIX]{x1D70C}$
for
$\unicode[STIX]{x1D70C}_{i}:=\exp (-\unicode[STIX]{x1D702}^{-(\text{i}+2)C_{4}})\unicode[STIX]{x1D70C}$
for
 $i=0,\ldots ,10$
, and using the bounds (8.12), (3.21) to justify the hypothesis (8.3). We conclude that for
$i=0,\ldots ,10$
, and using the bounds (8.12), (3.21) to justify the hypothesis (8.3). We conclude that for
![]() $c$
obeying (8.8) and
$c$
obeying (8.8) and
![]() $a$
obeying (8.13), we can find a natural number
$a$
obeying (8.13), we can find a natural number
![]() $k_{a,c}$
obeying (8.9), a set
$k_{a,c}$
obeying (8.9), a set
![]() $\tilde{S}_{a,c}$
with
$\tilde{S}_{a,c}$
with
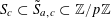 $S_{c}\subset \tilde{S}_{a,c}\subset \mathbb{Z}/p\mathbb{Z}$
obeying (8.10), a locally quadratic function
$S_{c}\subset \tilde{S}_{a,c}\subset \mathbb{Z}/p\mathbb{Z}$
obeying (8.10), a locally quadratic function
 $\unicode[STIX]{x1D719}_{a,c}:B(\tilde{S}_{a,c},\exp (-\unicode[STIX]{x1D702}^{-11C_{4}})\unicode[STIX]{x1D70C})\rightarrow \mathbb{R}/\mathbb{Z}$
, and a function
$\unicode[STIX]{x1D719}_{a,c}:B(\tilde{S}_{a,c},\exp (-\unicode[STIX]{x1D702}^{-11C_{4}})\unicode[STIX]{x1D70C})\rightarrow \mathbb{R}/\mathbb{Z}$
, and a function
 $\unicode[STIX]{x1D6FD}_{a,c}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D6FD}_{a,c}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}=n|\mathbf{a}=a,\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,|\mathbb{E}(f_{3}(a+6n+6k\mathbf{m})e(-\unicode[STIX]{x1D719}_{a,c}(\mathbf{m})-\unicode[STIX]{x1D6FD}_{a,c}(n)\mathbf{m})|\mathbf{a}=a,\mathbf{c}=c)|\gg \unicode[STIX]{x1D702}^{C_{2}/20}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}=n|\mathbf{a}=a,\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,|\mathbb{E}(f_{3}(a+6n+6k\mathbf{m})e(-\unicode[STIX]{x1D719}_{a,c}(\mathbf{m})-\unicode[STIX]{x1D6FD}_{a,c}(n)\mathbf{m})|\mathbf{a}=a,\mathbf{c}=c)|\gg \unicode[STIX]{x1D702}^{C_{2}/20}\nonumber\end{eqnarray}$$
if
![]() $\mathbf{n},\mathbf{m}$
are drawn independently and regularly from
$\mathbf{n},\mathbf{m}$
are drawn independently and regularly from
 $B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C}_{c})$
and
$B(S_{c},\exp (-\unicode[STIX]{x1D702}^{-2C_{4}})\unicode[STIX]{x1D70C}_{c})$
and
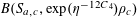 $B(S_{a,c},\exp (\unicode[STIX]{x1D702}^{-12C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively on the event
$B(S_{a,c},\exp (\unicode[STIX]{x1D702}^{-12C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively on the event
 $\mathbf{a}=a,\mathbf{c}=c$
. Taking expectations in
$\mathbf{a}=a,\mathbf{c}=c$
. Taking expectations in
![]() $\mathbf{a}$
(and choosing
$\mathbf{a}$
(and choosing
 $S_{a,c}=S_{c}$
,
$S_{a,c}=S_{c}$
,
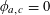 $\unicode[STIX]{x1D719}_{a,c}=0$
and
$\unicode[STIX]{x1D719}_{a,c}=0$
and
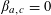 $\unicode[STIX]{x1D6FD}_{a,c}=0$
if (8.8) or (8.13) is not satisfied), we conclude that
$\unicode[STIX]{x1D6FD}_{a,c}=0$
if (8.8) or (8.13) is not satisfied), we conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n,a,c\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}=n,\mathbf{a}=a,\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,|\mathbb{E}(f_{3}(a+6n+6k\mathbf{m})e(-\unicode[STIX]{x1D719}_{a,c}(\mathbf{m})-\unicode[STIX]{x1D6FD}_{a,c}(n)\mathbf{m})|\mathbf{a}=a,\mathbf{c}=c)|\geqslant \unicode[STIX]{x1D702}^{C_{2}/10}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n,a,c\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}=n,\mathbf{a}=a,\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,|\mathbb{E}(f_{3}(a+6n+6k\mathbf{m})e(-\unicode[STIX]{x1D719}_{a,c}(\mathbf{m})-\unicode[STIX]{x1D6FD}_{a,c}(n)\mathbf{m})|\mathbf{a}=a,\mathbf{c}=c)|\geqslant \unicode[STIX]{x1D702}^{C_{2}/10}.\nonumber\end{eqnarray}$$
In particular, if we set
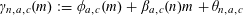 $\unicode[STIX]{x1D6FE}_{n,a,c}(m):=\unicode[STIX]{x1D719}_{a,c}(m)+\unicode[STIX]{x1D6FD}_{a,c}(n)m+\unicode[STIX]{x1D703}_{n,a,c}$
for a suitable phase
$\unicode[STIX]{x1D6FE}_{n,a,c}(m):=\unicode[STIX]{x1D719}_{a,c}(m)+\unicode[STIX]{x1D6FD}_{a,c}(n)m+\unicode[STIX]{x1D703}_{n,a,c}$
for a suitable phase
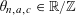 $\unicode[STIX]{x1D703}_{n,a,c}\in \mathbb{R}/\mathbb{Z}$
, then
$\unicode[STIX]{x1D703}_{n,a,c}\in \mathbb{R}/\mathbb{Z}$
, then
![]() $\unicode[STIX]{x1D6FE}_{n,a,c}$
is locally quadratic on
$\unicode[STIX]{x1D6FE}_{n,a,c}$
is locally quadratic on
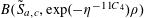 $B(\tilde{S}_{a,c},\exp (-\unicode[STIX]{x1D702}^{-11C_{4}})\unicode[STIX]{x1D70C})$
and
$B(\tilde{S}_{a,c},\exp (-\unicode[STIX]{x1D702}^{-11C_{4}})\unicode[STIX]{x1D70C})$
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Re}\mathop{\sum }_{n,a,c\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}=n,\mathbf{a}=a,\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathbb{E}(f_{3}(a+6n+6k\mathbf{m})e(-\unicode[STIX]{x1D6FE}_{n,a,c}(\mathbf{m}))|\mathbf{a}=a,\mathbf{c}=c)|\geqslant \unicode[STIX]{x1D702}^{C_{2}/10},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Re}\mathop{\sum }_{n,a,c\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}=n,\mathbf{a}=a,\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathbb{E}(f_{3}(a+6n+6k\mathbf{m})e(-\unicode[STIX]{x1D6FE}_{n,a,c}(\mathbf{m}))|\mathbf{a}=a,\mathbf{c}=c)|\geqslant \unicode[STIX]{x1D702}^{C_{2}/10},\nonumber\end{eqnarray}$$
giving the claim. ◻
Let
 $\mathbf{n},\mathbf{m},k_{a,c},\tilde{S}_{a,c},\unicode[STIX]{x1D6FE}_{n,a,c}$
be as in the above proposition. The conclusion (8.11) of Proposition 8.2 may be rewritten more compactly as
$\mathbf{n},\mathbf{m},k_{a,c},\tilde{S}_{a,c},\unicode[STIX]{x1D6FE}_{n,a,c}$
be as in the above proposition. The conclusion (8.11) of Proposition 8.2 may be rewritten more compactly as
 $$\begin{eqnarray}\text{Re}\,\mathbb{E}((f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})e(-\unicode[STIX]{x1D6FE}_{\mathbf{n},\mathbf{a},\mathbf{c}}(\mathbf{m})))\geqslant \unicode[STIX]{x1D702}^{C_{2}/10}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Re}\,\mathbb{E}((f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})e(-\unicode[STIX]{x1D6FE}_{\mathbf{n},\mathbf{a},\mathbf{c}}(\mathbf{m})))\geqslant \unicode[STIX]{x1D702}^{C_{2}/10}.\end{eqnarray}$$
We now introduce the modified random function
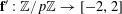 $\mathbf{f}^{\prime }:\mathbb{Z}/p\mathbb{Z}\rightarrow [-2,2]$
by the formula
$\mathbf{f}^{\prime }:\mathbb{Z}/p\mathbb{Z}\rightarrow [-2,2]$
by the formula
 $$\begin{eqnarray}\mathbf{f}^{\prime }(l):=\mathbf{f}(l)+\unicode[STIX]{x1D702}^{C_{2}/2}\cos \biggl(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}_{\boldsymbol{ n},\mathbf{a},\mathbf{c}}\biggl(\frac{l-\mathbf{a}-6\mathbf{n}}{6k_{\mathbf{a},\mathbf{c}}}\biggr)\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{f}^{\prime }(l):=\mathbf{f}(l)+\unicode[STIX]{x1D702}^{C_{2}/2}\cos \biggl(2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}_{\boldsymbol{ n},\mathbf{a},\mathbf{c}}\biggl(\frac{l-\mathbf{a}-6\mathbf{n}}{6k_{\mathbf{a},\mathbf{c}}}\biggr)\biggr),\end{eqnarray}$$
where we extend
![]() $\unicode[STIX]{x1D6FE}_{n,a,c}$
arbitrarily outside of
$\unicode[STIX]{x1D6FE}_{n,a,c}$
arbitrarily outside of
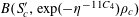 $B(S_{c}^{\prime },\exp (-\unicode[STIX]{x1D702}^{-11C_{4}})\unicode[STIX]{x1D70C}_{c})$
. Note from (8.9) and (3.21) that we can divide by
$B(S_{c}^{\prime },\exp (-\unicode[STIX]{x1D702}^{-11C_{4}})\unicode[STIX]{x1D70C}_{c})$
. Note from (8.9) and (3.21) that we can divide by
![]() $6k_{\mathbf{a},\mathbf{c}}$
in
$6k_{\mathbf{a},\mathbf{c}}$
in
![]() $\mathbb{Z}/p\mathbb{Z}$
without difficulty.
$\mathbb{Z}/p\mathbb{Z}$
without difficulty.
We claim that the function
![]() $\mathbf{f}^{\prime }$
is a little closer to
$\mathbf{f}^{\prime }$
is a little closer to
![]() $f$
than
$f$
than
![]() $\mathbf{f}$
is.
$\mathbf{f}$
is.
Lemma 8.3. We have
 $$\begin{eqnarray}\mathbb{E}|(f-\mathbf{f}^{\prime })(\mathbf{a}+6\mathbf{n}+6k_{\boldsymbol{ a},\mathbf{c}}\mathbf{m})|^{2}\leqslant \operatorname{Energy}(v)-\unicode[STIX]{x1D702}^{C_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}|(f-\mathbf{f}^{\prime })(\mathbf{a}+6\mathbf{n}+6k_{\boldsymbol{ a},\mathbf{c}}\mathbf{m})|^{2}\leqslant \operatorname{Energy}(v)-\unicode[STIX]{x1D702}^{C_{2}}.\end{eqnarray}$$
Proof. From (8.15) we have
 $$\begin{eqnarray}\mathbf{f}^{\prime }(\mathbf{a}+6\mathbf{n}+6k_{\boldsymbol{ a},\mathbf{c}}\mathbf{m})=\mathbf{f}(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})+\unicode[STIX]{x1D702}^{C_{2}/2}\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}_{\boldsymbol{ n},\mathbf{a},\mathbf{c}}(\mathbf{m})),\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{f}^{\prime }(\mathbf{a}+6\mathbf{n}+6k_{\boldsymbol{ a},\mathbf{c}}\mathbf{m})=\mathbf{f}(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})+\unicode[STIX]{x1D702}^{C_{2}/2}\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}_{\boldsymbol{ n},\mathbf{a},\mathbf{c}}(\mathbf{m})),\end{eqnarray}$$
and so
 $$\begin{eqnarray}\displaystyle & & \displaystyle |(f-\mathbf{f}^{\prime })(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =|(f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})|^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,2\unicode[STIX]{x1D702}^{C_{2}/2}\mathbb{E}(f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}_{\mathbf{n},\mathbf{a},\mathbf{c}}(\mathbf{m}))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\unicode[STIX]{x1D702}^{C_{2}}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |(f-\mathbf{f}^{\prime })(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =|(f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})|^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,2\unicode[STIX]{x1D702}^{C_{2}/2}\mathbb{E}(f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})\cos (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}_{\mathbf{n},\mathbf{a},\mathbf{c}}(\mathbf{m}))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(\unicode[STIX]{x1D702}^{C_{2}}).\end{eqnarray}$$
On the other hand, for any
![]() $(a,c)$
in the essential range of
$(a,c)$
in the essential range of
![]() $(\mathbf{a},\mathbf{c})$
, we may use Lemma 4.4 to compare
$(\mathbf{a},\mathbf{c})$
, we may use Lemma 4.4 to compare
![]() $\mathbf{n}$
with
$\mathbf{n}$
with
 $\mathbf{n}+k_{\mathbf{a},\mathbf{c}}\mathbf{m}$
, and conclude that
$\mathbf{n}+k_{\mathbf{a},\mathbf{c}}\mathbf{m}$
, and conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}(|(f-\mathbf{f})(a+6\mathbf{n}+6k_{a,c}\mathbf{m})|^{2}|\mathbf{a}=a,\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbb{E}(|(f-\mathbf{f})(a+6\mathbf{n})|^{2}|\mathbf{a}=a,\mathbf{c}=c)+O(\unicode[STIX]{x1D702}^{2C_{3}})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}(|(f-\mathbf{f})(a+6\mathbf{n}+6k_{a,c}\mathbf{m})|^{2}|\mathbf{a}=a,\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbb{E}(|(f-\mathbf{f})(a+6\mathbf{n})|^{2}|\mathbf{a}=a,\mathbf{c}=c)+O(\unicode[STIX]{x1D702}^{2C_{3}})\nonumber\end{eqnarray}$$
(for example), and hence on taking expectations in
![]() $\mathbf{a}$
$\mathbf{a}$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}(|(f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},c}\mathbf{m})|^{2}|\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbb{E}(|(f-\mathbf{f})(\mathbf{a}+6\mathbf{n})|^{2}|\mathbf{c}=c)+O(\unicode[STIX]{x1D702}^{2C_{3}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}(|(f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},c}\mathbf{m})|^{2}|\mathbf{c}=c)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathbb{E}(|(f-\mathbf{f})(\mathbf{a}+6\mathbf{n})|^{2}|\mathbf{c}=c)+O(\unicode[STIX]{x1D702}^{2C_{3}}).\nonumber\end{eqnarray}$$
Applying Lemma 4.4 again to compare
![]() $\mathbf{a}$
with
$\mathbf{a}$
with
![]() $\mathbf{a}+6\mathbf{n}$
, we conclude that
$\mathbf{a}+6\mathbf{n}$
, we conclude that
 $$\begin{eqnarray}\mathbb{E}(|(f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},c}\mathbf{m})|^{2}|\mathbf{c}=c)=\mathbb{E}(|(f-\mathbf{f})(\mathbf{a})|^{2}|\mathbf{c}=c)+O(\unicode[STIX]{x1D702}^{2C_{3}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}(|(f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},c}\mathbf{m})|^{2}|\mathbf{c}=c)=\mathbb{E}(|(f-\mathbf{f})(\mathbf{a})|^{2}|\mathbf{c}=c)+O(\unicode[STIX]{x1D702}^{2C_{3}}).\end{eqnarray}$$
and hence on taking averages in
![]() $\mathbf{c}$
$\mathbf{c}$
 $$\begin{eqnarray}\mathbb{E}(|(f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},c}\mathbf{m})|^{2}|\mathbf{c}=c)=\operatorname{Energy}(v)+O(\unicode[STIX]{x1D702}^{2C_{3}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}(|(f-\mathbf{f})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},c}\mathbf{m})|^{2}|\mathbf{c}=c)=\operatorname{Energy}(v)+O(\unicode[STIX]{x1D702}^{2C_{3}}).\end{eqnarray}$$
Taking expectations in (8.16) and using (8.15), (8.17), we obtain the claim. ◻
There is a very minor technical issue that
![]() $\mathbf{f}^{\prime }$
does not quite take values in
$\mathbf{f}^{\prime }$
does not quite take values in
![]() $[-1,1]$
, which is what is needed in the definition of an approximant. However, this is easily fixed by truncation, or more precisely by introducing the random function
$[-1,1]$
, which is what is needed in the definition of an approximant. However, this is easily fixed by truncation, or more precisely by introducing the random function
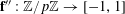 $\mathbf{f}^{\prime \prime }:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
defined by
$\mathbf{f}^{\prime \prime }:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
defined by
 $$\begin{eqnarray}\mathbf{f}^{\prime \prime }(l):=\min (\max (\mathbf{f}^{\prime }(l),-1),1).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{f}^{\prime \prime }(l):=\min (\max (\mathbf{f}^{\prime }(l),-1),1).\end{eqnarray}$$
Since
![]() $f(l)$
already lies in
$f(l)$
already lies in
![]() $[-1,1]$
, we see that
$[-1,1]$
, we see that
![]() $\mathbf{f}^{\prime \prime }(l)$
is at least as close to
$\mathbf{f}^{\prime \prime }(l)$
is at least as close to
![]() $f(l)$
as
$f(l)$
as
![]() $\mathbf{f}^{\prime }(l)$
is, thus we have the pointwise bound
$\mathbf{f}^{\prime }(l)$
is, thus we have the pointwise bound
 $$\begin{eqnarray}|(f-\mathbf{f}^{\prime \prime })(l)|\leqslant |(f-\mathbf{f}^{\prime })(l)|\end{eqnarray}$$
$$\begin{eqnarray}|(f-\mathbf{f}^{\prime \prime })(l)|\leqslant |(f-\mathbf{f}^{\prime })(l)|\end{eqnarray}$$
for any
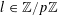 $l\in \mathbb{Z}/p\mathbb{Z}$
. From the above lemma, we thus have
$l\in \mathbb{Z}/p\mathbb{Z}$
. From the above lemma, we thus have
 $$\begin{eqnarray}\mathbb{E}|(f-\mathbf{f}^{\prime \prime })(\mathbf{a}+6\mathbf{n}+6k_{\boldsymbol{ a},\mathbf{c}}\mathbf{m})|^{2}\leqslant \operatorname{Energy}(v)-\unicode[STIX]{x1D702}^{C_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}|(f-\mathbf{f}^{\prime \prime })(\mathbf{a}+6\mathbf{n}+6k_{\boldsymbol{ a},\mathbf{c}}\mathbf{m})|^{2}\leqslant \operatorname{Energy}(v)-\unicode[STIX]{x1D702}^{C_{2}}.\end{eqnarray}$$
We can now construct the new structured approximant
 $$\begin{eqnarray}v^{\prime }=(C^{\prime },\mathbf{c}^{\prime },(n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }))_{c^{\prime }\in C^{\prime }},(G_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(F_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }})\end{eqnarray}$$
$$\begin{eqnarray}v^{\prime }=(C^{\prime },\mathbf{c}^{\prime },(n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }))_{c^{\prime }\in C^{\prime }},(G_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(F_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }},(\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime })_{c^{\prime }\in C^{\prime }})\end{eqnarray}$$
as follows. We write the dilated torus
![]() $G_{c}$
as
$G_{c}$
as
 $G_{c}=\prod _{i=1}^{\dim (G_{c})}\mathbb{R}/\unicode[STIX]{x1D706}_{i,c}\mathbb{Z}$
.
$G_{c}=\prod _{i=1}^{\dim (G_{c})}\mathbb{R}/\unicode[STIX]{x1D706}_{i,c}\mathbb{Z}$
.
-
(i) We set
 $C^{\prime }:=(\mathbb{Z}/p\mathbb{Z})\times (\mathbb{Z}/p\mathbb{Z})\times C$
and
$C^{\prime }:=(\mathbb{Z}/p\mathbb{Z})\times (\mathbb{Z}/p\mathbb{Z})\times C$
and
 $\mathbf{c}^{\prime }:=(\mathbf{n},\mathbf{a},\mathbf{c})$
.
$\mathbf{c}^{\prime }:=(\mathbf{n},\mathbf{a},\mathbf{c})$
. -
(ii) If
 $c^{\prime }=(n,a,c)$
is in
$c^{\prime }=(n,a,c)$
is in
 $C^{\prime }$
, we set
$C^{\prime }$
, we set  $$\begin{eqnarray}\displaystyle n_{c^{\prime }}^{\prime } & := & \displaystyle a+6n,\nonumber\\ \displaystyle S_{c^{\prime }}^{\prime } & := & \displaystyle (6k_{a,c})^{-1}\cdot \tilde{S}_{a,c},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime } & := & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-12C_{4}})\unicode[STIX]{x1D70C}_{c},\nonumber\\ \displaystyle G_{c^{\prime }}^{\prime } & := & \displaystyle \mathop{\prod }_{i=1}^{\dim (G_{c})}(\mathbb{R}/100\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})\times (\mathbb{R}/\mathbb{Z}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{c^{\prime }}^{\prime } & := & \displaystyle a+6n,\nonumber\\ \displaystyle S_{c^{\prime }}^{\prime } & := & \displaystyle (6k_{a,c})^{-1}\cdot \tilde{S}_{a,c},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime } & := & \displaystyle \exp (-\unicode[STIX]{x1D702}^{-12C_{4}})\unicode[STIX]{x1D70C}_{c},\nonumber\\ \displaystyle G_{c^{\prime }}^{\prime } & := & \displaystyle \mathop{\prod }_{i=1}^{\dim (G_{c})}(\mathbb{R}/100\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})\times (\mathbb{R}/\mathbb{Z}).\nonumber\end{eqnarray}$$
-
(iii) If
 $c^{\prime }=(n,a,c)$
is in
$c^{\prime }=(n,a,c)$
is in
 $C^{\prime }$
, we define
$C^{\prime }$
, we define
 $F_{c^{\prime }}^{\prime }:G_{c^{\prime }}^{\prime }\rightarrow [-1,1]$
to be the function for
$F_{c^{\prime }}^{\prime }:G_{c^{\prime }}^{\prime }\rightarrow [-1,1]$
to be the function for $$\begin{eqnarray}F_{c^{\prime }}^{\prime }(x,y):=\min (\max (F_{c}({\textstyle \frac{1}{100}}\cdot x)+\unicode[STIX]{x1D702}^{C_{2}/2}\cos (2\unicode[STIX]{x1D70B}y),-1),1)\end{eqnarray}$$
$$\begin{eqnarray}F_{c^{\prime }}^{\prime }(x,y):=\min (\max (F_{c}({\textstyle \frac{1}{100}}\cdot x)+\unicode[STIX]{x1D702}^{C_{2}/2}\cos (2\unicode[STIX]{x1D70B}y),-1),1)\end{eqnarray}$$
 $x\in \prod _{i=1}^{\dim (G_{c})}(\mathbb{R}/100\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})$
and
$x\in \prod _{i=1}^{\dim (G_{c})}(\mathbb{R}/100\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})$
and
 $y\in \mathbb{R}/\mathbb{Z}$
, where
$y\in \mathbb{R}/\mathbb{Z}$
, where
 $x\mapsto {\textstyle \frac{1}{100}}\cdot x$
is the obvious contraction map from
$x\mapsto {\textstyle \frac{1}{100}}\cdot x$
is the obvious contraction map from
 $\prod _{i=1}^{\dim (G_{c})}(\mathbb{R}/100\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})$
to
$\prod _{i=1}^{\dim (G_{c})}(\mathbb{R}/100\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})$
to
 $\prod _{i=1}^{\dim (G_{c})}(\mathbb{R}/\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})$
.
$\prod _{i=1}^{\dim (G_{c})}(\mathbb{R}/\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})$
.
-
(iv) If
 $c^{\prime }=(n,a,c)$
is in
$c^{\prime }=(n,a,c)$
is in
 $C^{\prime }$
, we define
$C^{\prime }$
, we define
 $\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }:n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime })\rightarrow G_{c^{\prime }}^{\prime }$
by the formula for
$\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }:n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime })\rightarrow G_{c^{\prime }}^{\prime }$
by the formula for $$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }(l):=\biggl(100\cdot \unicode[STIX]{x1D6EF}_{c}(l),\unicode[STIX]{x1D6FE}_{n,a,c}\biggl(\frac{l-a-6n}{6k_{a,c}}\biggr)\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }(l):=\biggl(100\cdot \unicode[STIX]{x1D6EF}_{c}(l),\unicode[STIX]{x1D6FE}_{n,a,c}\biggl(\frac{l-a-6n}{6k_{a,c}}\biggr)\biggr)\end{eqnarray}$$
 $l\in n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime })$
(which implies in particular that
$l\in n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime })$
(which implies in particular that
 $(l-a-6n)/6k_{a,c}\in B(\tilde{S}_{a,c},\exp (-\unicode[STIX]{x1D702}^{-12C_{4}})\unicode[STIX]{x1D70C}_{c})$
), where
$(l-a-6n)/6k_{a,c}\in B(\tilde{S}_{a,c},\exp (-\unicode[STIX]{x1D702}^{-12C_{4}})\unicode[STIX]{x1D70C}_{c})$
), where
 $x\mapsto 100\cdot x$
is the obvious dilation map from
$x\mapsto 100\cdot x$
is the obvious dilation map from
 $\prod _{i=1}^{\dim (G_{c})}(\mathbb{R}/\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})$
to
$\prod _{i=1}^{\dim (G_{c})}(\mathbb{R}/\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})$
to
 $\prod _{i=1}^{\dim (G_{c})}(\mathbb{R}/100\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})$
(the inverse of the map
$\prod _{i=1}^{\dim (G_{c})}(\mathbb{R}/100\unicode[STIX]{x1D706}_{i,c}\mathbb{Z})$
(the inverse of the map
 $x\mapsto {\textstyle \frac{1}{100}}\cdot x$
from part (iii)).
$x\mapsto {\textstyle \frac{1}{100}}\cdot x$
from part (iii)).
Since
![]() $F_{c}$
is
$F_{c}$
is
![]() $1$
-Lipschitz, it is easy to see (thanks to the contraction by
$1$
-Lipschitz, it is easy to see (thanks to the contraction by
![]() ${\textstyle \frac{1}{100}}$
) that
${\textstyle \frac{1}{100}}$
) that
![]() $F_{c^{\prime }}^{\prime }$
is also
$F_{c^{\prime }}^{\prime }$
is also
![]() $1$
-Lipschitz; similarly, as
$1$
-Lipschitz; similarly, as
![]() $\unicode[STIX]{x1D6EF}_{c}$
and
$\unicode[STIX]{x1D6EF}_{c}$
and
![]() $\unicode[STIX]{x1D6FE}_{n,a,c}$
are locally quadratic on
$\unicode[STIX]{x1D6FE}_{n,a,c}$
are locally quadratic on
 $n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})$
and
$n_{c}+B(S_{c},\unicode[STIX]{x1D70C}_{c})$
and
 $B(\tilde{S}_{a,c},\exp (\unicode[STIX]{x1D702}^{-11C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively, we see that
$B(\tilde{S}_{a,c},\exp (\unicode[STIX]{x1D702}^{-11C_{4}})\unicode[STIX]{x1D70C}_{c})$
respectively, we see that
![]() $\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }$
is also locally quadratic on
$\unicode[STIX]{x1D6EF}_{c^{\prime }}^{\prime }$
is also locally quadratic on
 $n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime })$
. From (8.15), (8.18), Definition 6.1, and the above constructions we see that
$n_{c^{\prime }}^{\prime }+B(S_{c^{\prime }}^{\prime },\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime })$
. From (8.15), (8.18), Definition 6.1, and the above constructions we see that
and hence by (8.19)
 $$\begin{eqnarray}\mathbb{E}|(f-\mathbf{f}_{v^{\prime }})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})|^{2}\leqslant \operatorname{Energy}(v)-\unicode[STIX]{x1D702}^{C_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}|(f-\mathbf{f}_{v^{\prime }})(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})|^{2}\leqslant \operatorname{Energy}(v)-\unicode[STIX]{x1D702}^{C_{2}}.\end{eqnarray}$$
From Definition 6.1 and the above constructions, we also see that
![]() $\mathbf{a}_{v^{\prime }}$
has the same distribution as
$\mathbf{a}_{v^{\prime }}$
has the same distribution as
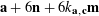 $\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m}$
(after conditioning to any positive probability event of the form
$\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m}$
(after conditioning to any positive probability event of the form
 $(\mathbf{n},\mathbf{a},\mathbf{c})=(n,a,c)$
), which gives the required energy decrement (6.15).
$(\mathbf{n},\mathbf{a},\mathbf{c})=(n,a,c)$
), which gives the required energy decrement (6.15).
The bound (6.10) follows from (8.10), while from construction we clearly have
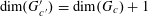 $\dim (G_{c^{\prime }}^{\prime })=\dim (G_{c})+1$
, which gives (6.11). Since we have
$\dim (G_{c^{\prime }}^{\prime })=\dim (G_{c})+1$
, which gives (6.11). Since we have
 $\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }:=\exp (-\unicode[STIX]{x1D702}^{-12C_{4}})\unicode[STIX]{x1D70C}_{c}$
, the bound (6.12) is clear; also, from (6.4) we have
$\unicode[STIX]{x1D70C}_{c^{\prime }}^{\prime }:=\exp (-\unicode[STIX]{x1D702}^{-12C_{4}})\unicode[STIX]{x1D70C}_{c}$
, the bound (6.12) is clear; also, from (6.4) we have
 $$\begin{eqnarray}\operatorname{vol}(G_{c^{\prime }}^{\prime })=100^{\dim (G_{c^{\prime }}^{\prime })}\operatorname{vol}(G_{c})\leqslant \exp (O(\unicode[STIX]{x1D702}^{-2C_{2}}))\operatorname{vol}(G_{c})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}(G_{c^{\prime }}^{\prime })=100^{\dim (G_{c^{\prime }}^{\prime })}\operatorname{vol}(G_{c})\leqslant \exp (O(\unicode[STIX]{x1D702}^{-2C_{2}}))\operatorname{vol}(G_{c})\end{eqnarray}$$
which gives (6.13). It remains to establish (6.14). By the definition of
![]() $\operatorname{Err}_{1}$
(just before (6.1)) and the triangle inequality, it suffices to show that
$\operatorname{Err}_{1}$
(just before (6.1)) and the triangle inequality, it suffices to show that
 $$\begin{eqnarray}|\mathbb{E}f(\mathbf{a}_{v^{\prime }})-\mathbb{E}f(\mathbf{a})|\leqslant \unicode[STIX]{x1D702}^{C_{3}}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f(\mathbf{a}_{v^{\prime }})-\mathbb{E}f(\mathbf{a})|\leqslant \unicode[STIX]{x1D702}^{C_{3}}.\end{eqnarray}$$
But as mentioned previously,
![]() $\mathbf{a}_{v^{\prime }}$
has the same distribution as
$\mathbf{a}_{v^{\prime }}$
has the same distribution as
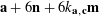 $\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m}$
, and by using Lemma 4.4 as in the proof of Lemma 8.3 we have
$\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m}$
, and by using Lemma 4.4 as in the proof of Lemma 8.3 we have
 $$\begin{eqnarray}\mathbb{E}f(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})=\mathbb{E}f(\mathbf{a})+O(\unicode[STIX]{x1D702}^{2C_{3}})\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f(\mathbf{a}+6\mathbf{n}+6k_{\mathbf{a},\mathbf{c}}\mathbf{m})=\mathbb{E}f(\mathbf{a})+O(\unicode[STIX]{x1D702}^{2C_{3}})\end{eqnarray}$$
giving the claim. This completes the proof of Theorem 6.6, assuming the local inverse Gowers norm theorem (Theorem 8.1).
9 Local inverse
 $U^{3}$
theorem
$U^{3}$
theorem
We now turn to the proof of Theorem 8.1, which is the last component needed in the proof of Theorem 1.1. Let us begin by recalling the setup of this theorem. We let
![]() $S$
be a subset of
$S$
be a subset of
![]() $\mathbb{Z}/p\mathbb{Z}$
, take a parameter
$\mathbb{Z}/p\mathbb{Z}$
, take a parameter
![]() $\unicode[STIX]{x1D702}$
satisfying
$\unicode[STIX]{x1D702}$
satisfying
 $0<\unicode[STIX]{x1D702}<{\textstyle \frac{1}{2}}$
, and define the quantity
$0<\unicode[STIX]{x1D702}<{\textstyle \frac{1}{2}}$
, and define the quantity
![]() $K$
by (8.1), thus
$K$
by (8.1), thus
 $$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D702}},\qquad |S|\leqslant K.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D702}},\qquad |S|\leqslant K.\end{eqnarray}$$
We suppose that
 $$\begin{eqnarray}0<\unicode[STIX]{x1D70C}_{10}<\cdots <\unicode[STIX]{x1D70C}_{0}<{\textstyle \frac{1}{2}}\end{eqnarray}$$
$$\begin{eqnarray}0<\unicode[STIX]{x1D70C}_{10}<\cdots <\unicode[STIX]{x1D70C}_{0}<{\textstyle \frac{1}{2}}\end{eqnarray}$$
are scales obeying the separation condition (8.2) and the largeness condition (8.3), and suppose that
 $f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
is a
$f:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
is a
![]() $1$
-bounded function obeying (8.4). Our task is to locate a natural number
$1$
-bounded function obeying (8.4). Our task is to locate a natural number
![]() $k$
with
$k$
with
 $k<\exp (K^{O(C_{1})})$
, a set
$k<\exp (K^{O(C_{1})})$
, a set
![]() $S^{\prime }$
with
$S^{\prime }$
with
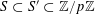 $S\subset S^{\prime }\subset \mathbb{Z}/p\mathbb{Z}$
obeying (8.5), a locally quadratic phase
$S\subset S^{\prime }\subset \mathbb{Z}/p\mathbb{Z}$
obeying (8.5), a locally quadratic phase
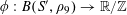 $\unicode[STIX]{x1D719}:B(S^{\prime },\unicode[STIX]{x1D70C}_{9})\rightarrow \mathbb{R}/\mathbb{Z}$
, and a function
$\unicode[STIX]{x1D719}:B(S^{\prime },\unicode[STIX]{x1D70C}_{9})\rightarrow \mathbb{R}/\mathbb{Z}$
, and a function
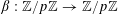 $\unicode[STIX]{x1D6FD}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
obeying (8.6). We will initially work at the scale
$\unicode[STIX]{x1D6FD}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
obeying (8.6). We will initially work at the scale
![]() $\unicode[STIX]{x1D70C}_{0}$
, but retreat to smaller scales as the argument progresses (mainly to ensure that the error terms in Lemma 4.4 are negligible), until we are working at the final scales
$\unicode[STIX]{x1D70C}_{0}$
, but retreat to smaller scales as the argument progresses (mainly to ensure that the error terms in Lemma 4.4 are negligible), until we are working at the final scales
![]() $\unicode[STIX]{x1D70C}_{9}$
and
$\unicode[STIX]{x1D70C}_{9}$
and
![]() $\unicode[STIX]{x1D70C}_{10}$
. Let us comment once more that the intermediate scales
$\unicode[STIX]{x1D70C}_{10}$
. Let us comment once more that the intermediate scales
 $\unicode[STIX]{x1D70C}_{3},\ldots ,\unicode[STIX]{x1D70C}_{8}$
play no role in the actual statement of Theorem 8.1.
$\unicode[STIX]{x1D70C}_{3},\ldots ,\unicode[STIX]{x1D70C}_{8}$
play no role in the actual statement of Theorem 8.1.
In this section, all sums will be over
![]() $\mathbb{Z}/p\mathbb{Z}$
unless otherwise stated.
$\mathbb{Z}/p\mathbb{Z}$
unless otherwise stated.
9.1 First step: associate a frequency
 $\unicode[STIX]{x1D709}(n_{2})$
to each derivative of
$\unicode[STIX]{x1D709}(n_{2})$
to each derivative of
 $f$
$f$
We now begin the (lengthy) proof of this theorem, which broadly follows the same inverse
![]() $U^{3}$
strategy in previous literature [Reference Gowers11, Reference Green and Tao14], but localized to a Bohr set, the key aim being to reduce the dependence of constants on the rank or radius of this Bohr set as much as possible.
$U^{3}$
strategy in previous literature [Reference Gowers11, Reference Green and Tao14], but localized to a Bohr set, the key aim being to reduce the dependence of constants on the rank or radius of this Bohr set as much as possible.
The first step is to use the local inverse
![]() $U^{2}$
theorem (Theorem 4.12) to associate a frequency
$U^{2}$
theorem (Theorem 4.12) to associate a frequency
 $\unicode[STIX]{x1D709}(n_{2})\in \mathbb{Z}/p\mathbb{Z}$
to many “derivatives”
$\unicode[STIX]{x1D709}(n_{2})\in \mathbb{Z}/p\mathbb{Z}$
to many “derivatives”
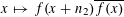 $x\mapsto f(x+n_{2})\overline{f(x)}$
of
$x\mapsto f(x+n_{2})\overline{f(x)}$
of
![]() $f$
.
$f$
.
Theorem 9.2. Let the notation and hypotheses be as in Theorem 8.1. Then there exists a set
 $\unicode[STIX]{x1D6FA}\subset B(S,2\unicode[STIX]{x1D70C}_{2})$
obeying the largeness condition
$\unicode[STIX]{x1D6FA}\subset B(S,2\unicode[STIX]{x1D70C}_{2})$
obeying the largeness condition
 $$\begin{eqnarray}\mathbb{P}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }\in \unicode[STIX]{x1D6FA})\geqslant \unicode[STIX]{x1D702}/4\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }\in \unicode[STIX]{x1D6FA})\geqslant \unicode[STIX]{x1D702}/4\end{eqnarray}$$
when
![]() $\mathbf{h}_{2},\mathbf{h}_{2}^{\prime }$
are drawn independently and regularly from
$\mathbf{h}_{2},\mathbf{h}_{2}^{\prime }$
are drawn independently and regularly from
 $B(S,\unicode[STIX]{x1D70C}_{2})$
, and a function
$B(S,\unicode[STIX]{x1D70C}_{2})$
, and a function
 $\unicode[STIX]{x1D709}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+n_{2})\overline{f}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(n_{2})\mathbf{n}_{1})|^{2}\geqslant \frac{\unicode[STIX]{x1D702}}{8}1_{\unicode[STIX]{x1D6FA}}(n_{2})\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+n_{2})\overline{f}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(n_{2})\mathbf{n}_{1})|^{2}\geqslant \frac{\unicode[STIX]{x1D702}}{8}1_{\unicode[STIX]{x1D6FA}}(n_{2})\end{eqnarray}$$
for all
 $n_{2}\in \mathbb{Z}/p\mathbb{Z}$
, and
$n_{2}\in \mathbb{Z}/p\mathbb{Z}$
, and
![]() $\mathbf{n}_{0},\mathbf{n}_{1}$
are drawn independently and regularly from
$\mathbf{n}_{0},\mathbf{n}_{1}$
are drawn independently and regularly from
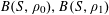 $B(S,\unicode[STIX]{x1D70C}_{0}),B(S,\unicode[STIX]{x1D70C}_{1})$
respectively.
$B(S,\unicode[STIX]{x1D70C}_{0}),B(S,\unicode[STIX]{x1D70C}_{1})$
respectively.
Proof. For each
 $n_{2}\in \mathbb{Z}/p\mathbb{Z}$
, let
$n_{2}\in \mathbb{Z}/p\mathbb{Z}$
, let
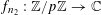 $f_{n_{2}}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
denote the
$f_{n_{2}}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
denote the
![]() $1$
-bounded function
$1$
-bounded function
 $$\begin{eqnarray}f_{n_{2}}(n):=f(n+n_{2})\overline{f}(n).\end{eqnarray}$$
$$\begin{eqnarray}f_{n_{2}}(n):=f(n+n_{2})\overline{f}(n).\end{eqnarray}$$
Then we may rewrite the left-hand side of (8.4) as
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}(\mathbf{h}_{0}+\mathbf{h}_{2}+\mathbf{h}_{1})\overline{f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}}(\mathbf{h}_{0}+\mathbf{h}_{2}+\mathbf{h}_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{2}+\mathbf{h}_{1})f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{2}+\mathbf{h}_{1}^{\prime })|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}(\mathbf{h}_{0}+\mathbf{h}_{2}+\mathbf{h}_{1})\overline{f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}}(\mathbf{h}_{0}+\mathbf{h}_{2}+\mathbf{h}_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{2}+\mathbf{h}_{1})f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{2}+\mathbf{h}_{1}^{\prime })|.\nonumber\end{eqnarray}$$
By Lemma 4.4 and (8.2), the random variables
![]() $\mathbf{h}_{0},\mathbf{h}_{0}^{\prime }$
differ in total variation from
$\mathbf{h}_{0},\mathbf{h}_{0}^{\prime }$
differ in total variation from
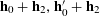 $\mathbf{h}_{0}+\mathbf{h}_{2},\mathbf{h}_{0}^{\prime }+\mathbf{h}_{2}$
respectively by at most
$\mathbf{h}_{0}+\mathbf{h}_{2},\mathbf{h}_{0}^{\prime }+\mathbf{h}_{2}$
respectively by at most
![]() $\unicode[STIX]{x1D702}/4$
(for example). We conclude that
$\unicode[STIX]{x1D702}/4$
(for example). We conclude that
 $$\begin{eqnarray}|\mathbb{E}f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime },0}}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f_{\boldsymbol{ h}_{2}-\mathbf{h}_{2}^{\prime }}}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\geqslant \unicode[STIX]{x1D702}/2.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime },0}}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f_{\boldsymbol{ h}_{2}-\mathbf{h}_{2}^{\prime }}}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\geqslant \unicode[STIX]{x1D702}/2.\end{eqnarray}$$
By the triangle inequality, the left-hand side is at most
 $$\begin{eqnarray}\mathop{\sum }_{h}\mathbb{P}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }=h)|\mathbb{E}f_{h}(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f_{h}}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f_{h}}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{h}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{h}\mathbb{P}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }=h)|\mathbb{E}f_{h}(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f_{h}}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f_{h}}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{h}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|.\end{eqnarray}$$
The inner expectation is bounded by
![]() $1$
. Applying Lemma 2.2 (with
$1$
. Applying Lemma 2.2 (with
 $\mathbf{a}=\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }$
), we conclude that there is a set
$\mathbf{a}=\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }$
), we conclude that there is a set
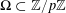 $\unicode[STIX]{x1D6FA}\subset \mathbb{Z}/p\mathbb{Z}$
obeying (9.2) such that
$\unicode[STIX]{x1D6FA}\subset \mathbb{Z}/p\mathbb{Z}$
obeying (9.2) such that
 $$\begin{eqnarray}|\mathbb{E}f_{n_{2}}(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f_{n_{2}}}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f_{n_{2}}}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{n_{2}}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\geqslant \unicode[STIX]{x1D702}/4\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f_{n_{2}}(\mathbf{h}_{0}+\mathbf{h}_{1})\overline{f_{n_{2}}}(\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })\overline{f_{n_{2}}}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{n_{2}}(\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\geqslant \unicode[STIX]{x1D702}/4\end{eqnarray}$$
for all
![]() $n_{2}\in \unicode[STIX]{x1D6FA}$
. Applying Theorem 4.12, we see that for each
$n_{2}\in \unicode[STIX]{x1D6FA}$
. Applying Theorem 4.12, we see that for each
![]() $n_{2}\in \unicode[STIX]{x1D6FA}$
, there exists
$n_{2}\in \unicode[STIX]{x1D6FA}$
, there exists
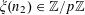 $\unicode[STIX]{x1D709}(n_{2})\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}(n_{2})\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}=n_{0})|\mathbb{E}f_{n_{2}}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(n_{2})\mathbf{n}_{1})|^{2}\geqslant \unicode[STIX]{x1D702}/8.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}\in \mathbb{Z}/p\mathbb{Z}}\mathbb{P}(\mathbf{n}=n_{0})|\mathbb{E}f_{n_{2}}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(n_{2})\mathbf{n}_{1})|^{2}\geqslant \unicode[STIX]{x1D702}/8.\end{eqnarray}$$
For
![]() $n_{2}\not \in \unicode[STIX]{x1D6FA}$
, we set
$n_{2}\not \in \unicode[STIX]{x1D6FA}$
, we set
![]() $\unicode[STIX]{x1D709}(n_{2})$
arbitrarily (e.g. to zero). The claim follows.◻
$\unicode[STIX]{x1D709}(n_{2})$
arbitrarily (e.g. to zero). The claim follows.◻
9.3 Second step:
 $\unicode[STIX]{x1D709}$
is approximately linear 1% of the time
$\unicode[STIX]{x1D709}$
is approximately linear 1% of the time
The next step, following Gowers [Reference Gowers11], is to obtain some approximate linearity control on the function
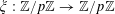 $\unicode[STIX]{x1D709}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
. Define an additive quadruple to be a quadruplet
$\unicode[STIX]{x1D709}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
. Define an additive quadruple to be a quadruplet
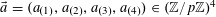 $\vec{a}=(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in (\mathbb{Z}/p\mathbb{Z})^{4}$
such that
$\vec{a}=(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in (\mathbb{Z}/p\mathbb{Z})^{4}$
such that
 $$\begin{eqnarray}a_{(1)}+a_{(2)}=a_{(3)}+a_{(4)},\end{eqnarray}$$
$$\begin{eqnarray}a_{(1)}+a_{(2)}=a_{(3)}+a_{(4)},\end{eqnarray}$$
and let
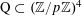 $\operatorname{Q}\subset (\mathbb{Z}/p\mathbb{Z})^{4}$
denote the space of all additive quadruples. We call an additive quadruple
$\operatorname{Q}\subset (\mathbb{Z}/p\mathbb{Z})^{4}$
denote the space of all additive quadruples. We call an additive quadruple
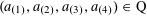 $(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in \operatorname{Q}$
bad if
$(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in \operatorname{Q}$
bad if
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}(a_{(1)})+\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}(a_{(3)})-\unicode[STIX]{x1D709}(a_{(4)})\Vert _{S}>\frac{K^{C_{1}}}{\unicode[STIX]{x1D70C}_{1}},\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}(a_{(1)})+\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}(a_{(3)})-\unicode[STIX]{x1D709}(a_{(4)})\Vert _{S}>\frac{K^{C_{1}}}{\unicode[STIX]{x1D70C}_{1}},\end{eqnarray}$$
where the word norm
![]() $\Vert \Vert _{S}$
was defined in Definition 4.5. Let
$\Vert \Vert _{S}$
was defined in Definition 4.5. Let
 $\operatorname{BQ}\subset \operatorname{Q}$
denote the space of all bad additive quadruples.
$\operatorname{BQ}\subset \operatorname{Q}$
denote the space of all bad additive quadruples.
Theorem 9.4. Let the notation and hypotheses be as in Theorem 8.1, and let
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
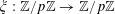 $\unicode[STIX]{x1D709}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
be as in Theorem 9.2. If
$\unicode[STIX]{x1D709}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
be as in Theorem 9.2. If
 $\mathbf{h}_{2},\mathbf{h}_{2}^{\prime },\mathbf{k}_{2},\mathbf{k}_{2}^{\prime }$
are drawn independently and regularly from
$\mathbf{h}_{2},\mathbf{h}_{2}^{\prime },\mathbf{k}_{2},\mathbf{k}_{2}^{\prime }$
are drawn independently and regularly from
 $B(S,\unicode[STIX]{x1D70C}_{2})$
, then with probability
$B(S,\unicode[STIX]{x1D70C}_{2})$
, then with probability
![]() $\gg \unicode[STIX]{x1D702}^{O(1)}$
, one has
$\gg \unicode[STIX]{x1D702}^{O(1)}$
, one has
 $$\begin{eqnarray}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime },\mathbf{k}_{2}-\mathbf{k}_{2}^{\prime },\mathbf{k}_{2}-\mathbf{h}_{2}^{\prime },\mathbf{h}_{2}-\mathbf{k}_{2}^{\prime })\in \unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ}).\end{eqnarray}$$
$$\begin{eqnarray}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime },\mathbf{k}_{2}-\mathbf{k}_{2}^{\prime },\mathbf{k}_{2}-\mathbf{h}_{2}^{\prime },\mathbf{h}_{2}-\mathbf{k}_{2}^{\prime })\in \unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ}).\end{eqnarray}$$
Proof. Let
![]() $\mathbf{n}_{0},\mathbf{n}_{1}$
be drawn independently and regularly from the Bohr sets
$\mathbf{n}_{0},\mathbf{n}_{1}$
be drawn independently and regularly from the Bohr sets
 $B(S,\unicode[STIX]{x1D70C}_{0})$
,
$B(S,\unicode[STIX]{x1D70C}_{0})$
,
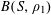 $B(S,\unicode[STIX]{x1D70C}_{1})$
respectively. From (9.3) we have
$B(S,\unicode[STIX]{x1D70C}_{1})$
respectively. From (9.3) we have
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+n_{2})\overline{f}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(n_{2})\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+n_{2})\overline{f}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(n_{2})\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}\end{eqnarray}$$
for any
![]() $n_{2}\in \unicode[STIX]{x1D6FA}$
. Using (9.2), we conclude that
$n_{2}\in \unicode[STIX]{x1D6FA}$
. Using (9.2), we conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0}}\mathop{\sum }_{n_{2}\in \unicode[STIX]{x1D6FA}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }=n_{2})|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+n_{2})\overline{f}(n_{0}+\mathbf{n}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}(-\unicode[STIX]{x1D709}(n_{2})\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}^{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0}}\mathop{\sum }_{n_{2}\in \unicode[STIX]{x1D6FA}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }=n_{2})|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+n_{2})\overline{f}(n_{0}+\mathbf{n}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}(-\unicode[STIX]{x1D709}(n_{2})\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}^{2},\nonumber\end{eqnarray}$$
where
![]() $\mathbf{h}_{2},\mathbf{h}_{2}^{\prime }$
are drawn independently and regularly from
$\mathbf{h}_{2},\mathbf{h}_{2}^{\prime }$
are drawn independently and regularly from
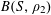 $B(S,\unicode[STIX]{x1D70C}_{2})$
, and are independent of
$B(S,\unicode[STIX]{x1D70C}_{2})$
, and are independent of
![]() $\mathbf{n}_{0},\mathbf{n}_{1}$
. By the pigeonhole principle, one can thus find
$\mathbf{n}_{0},\mathbf{n}_{1}$
. By the pigeonhole principle, one can thus find
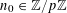 $n_{0}\in \mathbb{Z}/p\mathbb{Z}$
such that
$n_{0}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\mathop{\sum }_{n_{2}\in \unicode[STIX]{x1D6FA}}\mathbb{P}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }=n_{2})|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+n_{2})\overline{f}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(n_{2})\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{2}\in \unicode[STIX]{x1D6FA}}\mathbb{P}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }=n_{2})|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+n_{2})\overline{f}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(n_{2})\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}^{2}.\end{eqnarray}$$
We can rewrite the left-hand side as
 $$\begin{eqnarray}\mathbb{E}F_{n_{0}}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime })f(n_{0}+\mathbf{n}_{1}+\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime })\overline{f}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime })\mathbf{n}_{1})\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}F_{n_{0}}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime })f(n_{0}+\mathbf{n}_{1}+\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime })\overline{f}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime })\mathbf{n}_{1})\end{eqnarray}$$
for some
![]() $1$
-bounded function
$1$
-bounded function
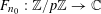 $F_{n_{0}}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
depending on
$F_{n_{0}}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
depending on
![]() $n_{0}$
. Using Lemma 4.4 to compare
$n_{0}$
. Using Lemma 4.4 to compare
![]() $\mathbf{n}_{1}$
with
$\mathbf{n}_{1}$
with
![]() $\mathbf{n}_{1}+\mathbf{h}_{2}^{\prime }$
, we conclude that
$\mathbf{n}_{1}+\mathbf{h}_{2}^{\prime }$
, we conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}F_{n_{0}}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime })f(n_{0}+\mathbf{n}_{1}+\mathbf{h}_{2})\overline{f}(n_{0}+\mathbf{n}_{1}+\mathbf{h}_{2}^{\prime })e_{p}(-\unicode[STIX]{x1D709}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime })(\mathbf{n}_{1}+\mathbf{h}_{2}^{\prime }))|\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}F_{n_{0}}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime })f(n_{0}+\mathbf{n}_{1}+\mathbf{h}_{2})\overline{f}(n_{0}+\mathbf{n}_{1}+\mathbf{h}_{2}^{\prime })e_{p}(-\unicode[STIX]{x1D709}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime })(\mathbf{n}_{1}+\mathbf{h}_{2}^{\prime }))|\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{2}.\nonumber\end{eqnarray}$$
We rearrange the left-hand side as
 $$\begin{eqnarray}\mathop{\sum }_{n_{1}}\mathbb{P}(\mathbf{n}_{1}=n_{1})\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}_{2})\overline{f}(n_{0}+n_{1}+\mathbf{h}_{2}^{\prime })G_{n_{0},n_{1}}(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{1}}\mathbb{P}(\mathbf{n}_{1}=n_{1})\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}_{2})\overline{f}(n_{0}+n_{1}+\mathbf{h}_{2}^{\prime })G_{n_{0},n_{1}}(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })\end{eqnarray}$$
where
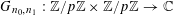 $G_{n_{0},n_{1}}:\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
is the
$G_{n_{0},n_{1}}:\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
is the
![]() $1$
-bounded function
$1$
-bounded function
 $$\begin{eqnarray}G_{n_{0},n_{1}}(h_{2},h_{2}^{\prime }):=F_{n_{0}}(h_{2}-h_{2}^{\prime })e_{p}(-\unicode[STIX]{x1D709}(h_{2}-h_{2}^{\prime })(n_{1}+h_{2}^{\prime })).\end{eqnarray}$$
$$\begin{eqnarray}G_{n_{0},n_{1}}(h_{2},h_{2}^{\prime }):=F_{n_{0}}(h_{2}-h_{2}^{\prime })e_{p}(-\unicode[STIX]{x1D709}(h_{2}-h_{2}^{\prime })(n_{1}+h_{2}^{\prime })).\end{eqnarray}$$
By Hölder’s inequality, we conclude that
 $$\begin{eqnarray}\mathop{\sum }_{n_{1}}\mathbb{P}(\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}_{2})\overline{f}(n_{0}+n_{1}+\mathbf{h}_{2}^{\prime })G_{n_{0},n_{1}}(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })|^{4}\gg \unicode[STIX]{x1D702}^{O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{1}}\mathbb{P}(\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}_{2})\overline{f}(n_{0}+n_{1}+\mathbf{h}_{2}^{\prime })G_{n_{0},n_{1}}(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })|^{4}\gg \unicode[STIX]{x1D702}^{O(1)}.\end{eqnarray}$$
From this point onward we cease to keep careful track of powers of
![]() $\unicode[STIX]{x1D702}$
. On the other hand, by using two applications of Lemma 2.1 to eliminate the
$\unicode[STIX]{x1D702}$
. On the other hand, by using two applications of Lemma 2.1 to eliminate the
![]() $1$
-bounded functions
$1$
-bounded functions
![]() $f$
, we have
$f$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}_{2})\overline{f}(n_{0}+n_{1}+\mathbf{h}_{2}^{\prime })G_{n_{0},n_{1}}(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })|^{4}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathbb{E}G_{n_{0},n_{1}}(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })\overline{G_{n_{0},n_{1}}}(\mathbf{h}_{2},\mathbf{k}_{2}^{\prime })\overline{G_{n_{0},n_{1}}}(\mathbf{k}_{2},\mathbf{h}_{2}^{\prime })G_{n_{0},n_{1}}(\mathbf{k}_{2},\mathbf{k}_{2}^{\prime })\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}_{2})\overline{f}(n_{0}+n_{1}+\mathbf{h}_{2}^{\prime })G_{n_{0},n_{1}}(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })|^{4}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathbb{E}G_{n_{0},n_{1}}(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })\overline{G_{n_{0},n_{1}}}(\mathbf{h}_{2},\mathbf{k}_{2}^{\prime })\overline{G_{n_{0},n_{1}}}(\mathbf{k}_{2},\mathbf{h}_{2}^{\prime })G_{n_{0},n_{1}}(\mathbf{k}_{2},\mathbf{k}_{2}^{\prime })\nonumber\end{eqnarray}$$
where
![]() $(\mathbf{k}_{2},\mathbf{k}_{2}^{\prime })$
is an independent copy of
$(\mathbf{k}_{2},\mathbf{k}_{2}^{\prime })$
is an independent copy of
![]() $(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })$
. We thus have
$(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })$
. We thus have
 $$\begin{eqnarray}\mathbb{E}G_{n_{0},\mathbf{n}_{1}}(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })\overline{G_{n_{0},\mathbf{n}_{1}}}(\mathbf{h}_{2},\mathbf{k}_{2}^{\prime })\overline{G_{n_{0},\mathbf{n}_{1}}}(\mathbf{k}_{2},\mathbf{h}_{2}^{\prime })G_{n_{0},\mathbf{n}_{1}}(\mathbf{k}_{2},\mathbf{k}_{2}^{\prime })\gg \unicode[STIX]{x1D702}^{O(1)}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}G_{n_{0},\mathbf{n}_{1}}(\mathbf{h}_{2},\mathbf{h}_{2}^{\prime })\overline{G_{n_{0},\mathbf{n}_{1}}}(\mathbf{h}_{2},\mathbf{k}_{2}^{\prime })\overline{G_{n_{0},\mathbf{n}_{1}}}(\mathbf{k}_{2},\mathbf{h}_{2}^{\prime })G_{n_{0},\mathbf{n}_{1}}(\mathbf{k}_{2},\mathbf{k}_{2}^{\prime })\gg \unicode[STIX]{x1D702}^{O(1)}\end{eqnarray}$$
which by the triangle inequality and (9.7) gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{h_{2},k_{2},h_{2}^{\prime },k_{2}^{\prime }}1_{h_{2}-h_{2}^{\prime },k_{2}-k_{2}^{\prime },k_{2}-h_{2}^{\prime },h_{2}-k_{2}^{\prime }\in \unicode[STIX]{x1D6FA}}\mathbb{P}(\mathbf{h}_{2}=h_{2};\mathbf{k}_{2}=k_{2};\mathbf{h}_{2}^{\prime }=h_{2}^{\prime };\mathbf{k}_{2}^{\prime }=k_{2}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,|\mathbb{E}e_{p}(-(\unicode[STIX]{x1D709}(h_{2}-h_{2}^{\prime })+\unicode[STIX]{x1D709}(k_{2}-k_{2}^{\prime })-\unicode[STIX]{x1D709}(k_{2}-h_{2}^{\prime })-\unicode[STIX]{x1D709}(h_{2}-k_{2}^{\prime }))\mathbf{n}_{1})|\nonumber\\ \displaystyle & & \displaystyle \qquad \gg \unicode[STIX]{x1D702}^{O(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{h_{2},k_{2},h_{2}^{\prime },k_{2}^{\prime }}1_{h_{2}-h_{2}^{\prime },k_{2}-k_{2}^{\prime },k_{2}-h_{2}^{\prime },h_{2}-k_{2}^{\prime }\in \unicode[STIX]{x1D6FA}}\mathbb{P}(\mathbf{h}_{2}=h_{2};\mathbf{k}_{2}=k_{2};\mathbf{h}_{2}^{\prime }=h_{2}^{\prime };\mathbf{k}_{2}^{\prime }=k_{2}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \times \,|\mathbb{E}e_{p}(-(\unicode[STIX]{x1D709}(h_{2}-h_{2}^{\prime })+\unicode[STIX]{x1D709}(k_{2}-k_{2}^{\prime })-\unicode[STIX]{x1D709}(k_{2}-h_{2}^{\prime })-\unicode[STIX]{x1D709}(h_{2}-k_{2}^{\prime }))\mathbf{n}_{1})|\nonumber\\ \displaystyle & & \displaystyle \qquad \gg \unicode[STIX]{x1D702}^{O(1)}.\nonumber\end{eqnarray}$$
By Lemma 2.2, we conclude that with probability
 $\gg \unicode[STIX]{x1D702}^{O(1)}$
, the tuple
$\gg \unicode[STIX]{x1D702}^{O(1)}$
, the tuple
 $(\mathbf{h}_{2},\mathbf{k}_{2},\mathbf{h}_{2}^{\prime },\mathbf{k}_{2}^{\prime })$
attains a value
$(\mathbf{h}_{2},\mathbf{k}_{2},\mathbf{h}_{2}^{\prime },\mathbf{k}_{2}^{\prime })$
attains a value
 $(h_{2},k_{2},h_{2}^{\prime },k_{2}^{\prime })$
for which
$(h_{2},k_{2},h_{2}^{\prime },k_{2}^{\prime })$
for which
 $$\begin{eqnarray}h_{2}-h_{2}^{\prime },k_{2}-k_{2}^{\prime },h_{2}-k_{2}^{\prime },k_{2}-h_{2}^{\prime }\in \unicode[STIX]{x1D6FA}\end{eqnarray}$$
$$\begin{eqnarray}h_{2}-h_{2}^{\prime },k_{2}-k_{2}^{\prime },h_{2}-k_{2}^{\prime },k_{2}-h_{2}^{\prime }\in \unicode[STIX]{x1D6FA}\end{eqnarray}$$
and
 $$\begin{eqnarray}|\mathbb{E}e_{p}(-(\unicode[STIX]{x1D709}(h_{2}-h_{2}^{\prime })\,+\,\unicode[STIX]{x1D709}(k_{2}-k_{2}^{\prime })-\unicode[STIX]{x1D709}(k_{2}-h_{2}^{\prime })-\unicode[STIX]{x1D709}(h_{2}-k_{2}^{\prime }))\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}^{O(1)}\gg K^{-O(1)}\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}e_{p}(-(\unicode[STIX]{x1D709}(h_{2}-h_{2}^{\prime })\,+\,\unicode[STIX]{x1D709}(k_{2}-k_{2}^{\prime })-\unicode[STIX]{x1D709}(k_{2}-h_{2}^{\prime })-\unicode[STIX]{x1D709}(h_{2}-k_{2}^{\prime }))\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}^{O(1)}\gg K^{-O(1)}\end{eqnarray}$$
thanks to (9.1). Since
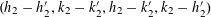 $(h_{2}-h_{2}^{\prime },k_{2}-k_{2}^{\prime },h_{2}-k_{2}^{\prime },k_{2}-h_{2}^{\prime })$
is an additive quadruple, the claim now follows from Lemma 4.7, (8.2), and (9.1).◻
$(h_{2}-h_{2}^{\prime },k_{2}-k_{2}^{\prime },h_{2}-k_{2}^{\prime },k_{2}-h_{2}^{\prime })$
is an additive quadruple, the claim now follows from Lemma 4.7, (8.2), and (9.1).◻
We localize this claim slightly, though for notational reasons we will not move from
![]() $\unicode[STIX]{x1D70C}_{2}$
immediately to
$\unicode[STIX]{x1D70C}_{2}$
immediately to
![]() $\unicode[STIX]{x1D70C}_{3}$
and beyond, but instead first work in some intermediate scales between
$\unicode[STIX]{x1D70C}_{3}$
and beyond, but instead first work in some intermediate scales between
![]() $\unicode[STIX]{x1D70C}_{2}$
and
$\unicode[STIX]{x1D70C}_{2}$
and
![]() $\unicode[STIX]{x1D70C}_{3}$
. For any natural number
$\unicode[STIX]{x1D70C}_{3}$
. For any natural number
![]() $j$
, define
$j$
, define
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{2,j}:=\exp (-C_{1}jK)\unicode[STIX]{x1D70C}_{2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{2,j}:=\exp (-C_{1}jK)\unicode[STIX]{x1D70C}_{2},\end{eqnarray}$$
thus
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{2}=\unicode[STIX]{x1D70C}_{2,0}>\unicode[STIX]{x1D70C}_{2,1}>\cdots >\unicode[STIX]{x1D70C}_{2,j}\geqslant \unicode[STIX]{x1D70C}_{3}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{2}=\unicode[STIX]{x1D70C}_{2,0}>\unicode[STIX]{x1D70C}_{2,1}>\cdots >\unicode[STIX]{x1D70C}_{2,j}\geqslant \unicode[STIX]{x1D70C}_{3}\end{eqnarray}$$
if (for example)
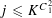 $j\leqslant K^{C_{1}^{2}}$
.
$j\leqslant K^{C_{1}^{2}}$
.
It will be necessary to break the symmetry between the four components of an additive quadruple, by restricting the second component to a tiny Bohr set, the third component to a larger Bohr set, and the first and fourth components to an even larger Bohr set. More precisely, given an additive quadruple
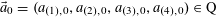 $\vec{a}_{0}=(a_{(1),0},a_{(2),0},a_{(3),0},a_{(4),0})\in \operatorname{Q}$
, a subset
$\vec{a}_{0}=(a_{(1),0},a_{(2),0},a_{(3),0},a_{(4),0})\in \operatorname{Q}$
, a subset
 $S^{\prime }\subset \mathbb{Z}/p\mathbb{Z}$
, and radii
$S^{\prime }\subset \mathbb{Z}/p\mathbb{Z}$
, and radii
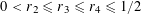 $0<r_{2}\leqslant r_{3}\leqslant r_{4}\leqslant 1/2$
, we say that a random additive quadruple
$0<r_{2}\leqslant r_{3}\leqslant r_{4}\leqslant 1/2$
, we say that a random additive quadruple
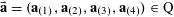 $\vec{\mathbf{a}}=(\mathbf{a}_{(1)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)})\in \operatorname{Q}$
is centred at
$\vec{\mathbf{a}}=(\mathbf{a}_{(1)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)})\in \operatorname{Q}$
is centred at
![]() $\vec{a}_{0}$
with frequencies
$\vec{a}_{0}$
with frequencies
![]() $S^{\prime }$
and scales
$S^{\prime }$
and scales
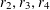 $r_{2},r_{3},r_{4}$
if
$r_{2},r_{3},r_{4}$
if
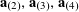 $\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)}$
are drawn independently and regularly from
$\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)}$
are drawn independently and regularly from
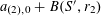 $a_{(2),0}+B(S^{\prime },r_{2})$
,
$a_{(2),0}+B(S^{\prime },r_{2})$
,
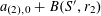 $a_{(2),0}+B(S^{\prime },r_{2})$
, and
$a_{(2),0}+B(S^{\prime },r_{2})$
, and
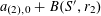 $a_{(2),0}+B(S^{\prime },r_{2})$
respectively. Note that this property also describes the distribution of
$a_{(2),0}+B(S^{\prime },r_{2})$
respectively. Note that this property also describes the distribution of
![]() $\mathbf{a}_{(1)}$
, since we have the constraint
$\mathbf{a}_{(1)}$
, since we have the constraint
 $$\begin{eqnarray}\mathbf{a}_{(1)}=\mathbf{a}_{(3)}+\mathbf{a}_{(4)}-\mathbf{a}_{(2)}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{a}_{(1)}=\mathbf{a}_{(3)}+\mathbf{a}_{(4)}-\mathbf{a}_{(2)}.\end{eqnarray}$$
In practice,
![]() $r_{4}$
will be much larger than
$r_{4}$
will be much larger than
![]() $r_{2},r_{3}$
, so (by Lemma 4.4)
$r_{2},r_{3}$
, so (by Lemma 4.4)
![]() $\mathbf{a}_{(1)}$
will be approximately regularly drawn from
$\mathbf{a}_{(1)}$
will be approximately regularly drawn from
 $a_{(1),0}+B(S^{\prime },r_{4})$
, but will be highly coupled to the other three components of the quadruple (in particular, it will stay close to
$a_{(1),0}+B(S^{\prime },r_{4})$
, but will be highly coupled to the other three components of the quadruple (in particular, it will stay close to
![]() $\mathbf{a}_{(4)}$
). We thus see that for
$\mathbf{a}_{(4)}$
). We thus see that for
 $i=1,2,3,4$
, each
$i=1,2,3,4$
, each
![]() $\mathbf{a}_{(i)}$
is either exactly or approximately drawn regularly from
$\mathbf{a}_{(i)}$
is either exactly or approximately drawn regularly from
 $a_{(i),0}+B(S^{\prime },r_{l_{i}})$
, where
$a_{(i),0}+B(S^{\prime },r_{l_{i}})$
, where
 $l_{i}\in \{0,1,2\}$
is the quantity defined by the formulae
$l_{i}\in \{0,1,2\}$
is the quantity defined by the formulae
 $$\begin{eqnarray}l_{1}:=0;\qquad l_{2}:=2;\qquad l_{3}:=1;\qquad l_{4}:=0.\end{eqnarray}$$
$$\begin{eqnarray}l_{1}:=0;\qquad l_{2}:=2;\qquad l_{3}:=1;\qquad l_{4}:=0.\end{eqnarray}$$
Corollary 9.5. Let the notation and hypotheses be as in Theorem 8.1, and let
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D709}$
be as in Theorem 9.2. Then there exists a random additive quadruple
$\unicode[STIX]{x1D709}$
be as in Theorem 9.2. Then there exists a random additive quadruple
![]() $\vec{\mathbf{a}}\in \operatorname{Q}$
centred at some quadruple
$\vec{\mathbf{a}}\in \operatorname{Q}$
centred at some quadruple
![]() $\vec{a}_{0}\in \operatorname{Q}$
with frequencies
$\vec{a}_{0}\in \operatorname{Q}$
with frequencies
![]() $S$
and scales
$S$
and scales
 $\unicode[STIX]{x1D70C}_{2,2},\unicode[STIX]{x1D70C}_{2,1},\unicode[STIX]{x1D70C}_{2,0}$
, such that
$\unicode[STIX]{x1D70C}_{2,2},\unicode[STIX]{x1D70C}_{2,1},\unicode[STIX]{x1D70C}_{2,0}$
, such that
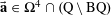 $\vec{\mathbf{a}}\in \unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})$
with probability
$\vec{\mathbf{a}}\in \unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})$
with probability
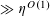 $\gg \unicode[STIX]{x1D702}^{O(1)}$
.
$\gg \unicode[STIX]{x1D702}^{O(1)}$
.
Proof. Let
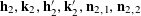 $\mathbf{h}_{2},\mathbf{k}_{2},\mathbf{h}_{2}^{\prime },\mathbf{k}_{2}^{\prime },\mathbf{n}_{2,1},\mathbf{n}_{2,2}$
be drawn independently and regularly from
$\mathbf{h}_{2},\mathbf{k}_{2},\mathbf{h}_{2}^{\prime },\mathbf{k}_{2}^{\prime },\mathbf{n}_{2,1},\mathbf{n}_{2,2}$
be drawn independently and regularly from
 $B(S,\unicode[STIX]{x1D70C}_{2,0})$
,
$B(S,\unicode[STIX]{x1D70C}_{2,0})$
,
 $B(S,\unicode[STIX]{x1D70C}_{2,0})$
,
$B(S,\unicode[STIX]{x1D70C}_{2,0})$
,
 $B(S,\unicode[STIX]{x1D70C}_{2,0})$
,
$B(S,\unicode[STIX]{x1D70C}_{2,0})$
,
 $B(S,\unicode[STIX]{x1D70C}_{2,0})$
,
$B(S,\unicode[STIX]{x1D70C}_{2,0})$
,
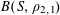 $B(S,\unicode[STIX]{x1D70C}_{2,1})$
and
$B(S,\unicode[STIX]{x1D70C}_{2,1})$
and
 $B(S,\unicode[STIX]{x1D70C}_{2,2})$
respectively. From Theorem 9.4, we have
$B(S,\unicode[STIX]{x1D70C}_{2,2})$
respectively. From Theorem 9.4, we have
 $$\begin{eqnarray}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime },\mathbf{k}_{2}-\mathbf{k}_{2}^{\prime },\mathbf{h}_{2}-\mathbf{k}_{2}^{\prime },\mathbf{k}_{2}-\mathbf{h}_{2}^{\prime })\in \unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})\end{eqnarray}$$
$$\begin{eqnarray}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime },\mathbf{k}_{2}-\mathbf{k}_{2}^{\prime },\mathbf{h}_{2}-\mathbf{k}_{2}^{\prime },\mathbf{k}_{2}-\mathbf{h}_{2}^{\prime })\in \unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})\end{eqnarray}$$
with probability
![]() $\gg \unicode[STIX]{x1D702}^{O(1)}$
. Using Lemma 4.4, we may replace
$\gg \unicode[STIX]{x1D702}^{O(1)}$
. Using Lemma 4.4, we may replace
![]() $\mathbf{k}_{2}^{\prime }$
by
$\mathbf{k}_{2}^{\prime }$
by
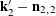 $\mathbf{k}_{2}^{\prime }-\mathbf{n}_{2,2}$
, and similarly replace
$\mathbf{k}_{2}^{\prime }-\mathbf{n}_{2,2}$
, and similarly replace
![]() $\mathbf{h}_{2}$
by
$\mathbf{h}_{2}$
by
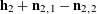 $\mathbf{h}_{2}+\mathbf{n}_{2,1}-\mathbf{n}_{2,2}$
, to conclude that
$\mathbf{h}_{2}+\mathbf{n}_{2,1}-\mathbf{n}_{2,2}$
, to conclude that
 $$\begin{eqnarray}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }+\mathbf{n}_{2,1},\mathbf{k}_{2}-\mathbf{k}_{2}^{\prime }+\mathbf{n}_{2,2},\mathbf{h}_{2}-\mathbf{k}_{2}^{\prime }+\mathbf{n}_{2,1},\mathbf{k}_{2}-\mathbf{h}_{2}^{\prime })\in \unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})\end{eqnarray}$$
$$\begin{eqnarray}(\mathbf{h}_{2}-\mathbf{h}_{2}^{\prime }+\mathbf{n}_{2,1},\mathbf{k}_{2}-\mathbf{k}_{2}^{\prime }+\mathbf{n}_{2,2},\mathbf{h}_{2}-\mathbf{k}_{2}^{\prime }+\mathbf{n}_{2,1},\mathbf{k}_{2}-\mathbf{h}_{2}^{\prime })\in \unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})\end{eqnarray}$$
with probability
![]() $\gg \unicode[STIX]{x1D702}^{O(1)}$
. By the pigeonhole principle, we may thus find
$\gg \unicode[STIX]{x1D702}^{O(1)}$
. By the pigeonhole principle, we may thus find
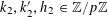 $k_{2},k_{2}^{\prime },h_{2}\in \mathbb{Z}/p\mathbb{Z}$
such that
$k_{2},k_{2}^{\prime },h_{2}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}(h_{2}-\mathbf{h}_{2}^{\prime }+\mathbf{n}_{2,1},k_{2}-k_{2}^{\prime }+\mathbf{n}_{2,2},h_{2}-k_{2}^{\prime }+\mathbf{n}_{2,1},k_{2}-\mathbf{h}_{2}^{\prime })\in \unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})\end{eqnarray}$$
$$\begin{eqnarray}(h_{2}-\mathbf{h}_{2}^{\prime }+\mathbf{n}_{2,1},k_{2}-k_{2}^{\prime }+\mathbf{n}_{2,2},h_{2}-k_{2}^{\prime }+\mathbf{n}_{2,1},k_{2}-\mathbf{h}_{2}^{\prime })\in \unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})\end{eqnarray}$$
with probability
![]() $\gg \unicode[STIX]{x1D702}^{O(1)}$
. The left-hand side is an additive quadruple centred at
$\gg \unicode[STIX]{x1D702}^{O(1)}$
. The left-hand side is an additive quadruple centred at
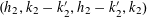 $(h_{2},k_{2}-k_{2}^{\prime },h_{2}-k_{2}^{\prime },k_{2})$
with frequencies
$(h_{2},k_{2}-k_{2}^{\prime },h_{2}-k_{2}^{\prime },k_{2})$
with frequencies
![]() $S$
and scales
$S$
and scales
 $\unicode[STIX]{x1D70C}_{2,2},\unicode[STIX]{x1D70C}_{2,1},\unicode[STIX]{x1D70C}_{2,0}$
, and the claim follows.◻
$\unicode[STIX]{x1D70C}_{2,2},\unicode[STIX]{x1D70C}_{2,1},\unicode[STIX]{x1D70C}_{2,0}$
, and the claim follows.◻
9.6 Third step:
 $\unicode[STIX]{x1D709}$
is approximately linear 99% of the time on a rough set
$\unicode[STIX]{x1D709}$
is approximately linear 99% of the time on a rough set
The next general step in the standard inverse
![]() $U^{3}$
argument is to upgrade this weak additive structure, which is of a “1 percent” nature, to a more robust “99 percent” additive structure. There are two basic ways to proceed here. The first way is to invoke the Balog–Szemerédi–Gowers theorem [Reference Balog and Szemerédi1, Reference Gowers11], followed by standard sum set estimates including Freiman’s theorem (see e.g. [Reference Tao and Vu33, Ch. 2]). It is likely that this approach will eventually work here, but these results need to be localized efficiently to Bohr sets, and also to allow for the fact that
$U^{3}$
argument is to upgrade this weak additive structure, which is of a “1 percent” nature, to a more robust “99 percent” additive structure. There are two basic ways to proceed here. The first way is to invoke the Balog–Szemerédi–Gowers theorem [Reference Balog and Szemerédi1, Reference Gowers11], followed by standard sum set estimates including Freiman’s theorem (see e.g. [Reference Tao and Vu33, Ch. 2]). It is likely that this approach will eventually work here, but these results need to be localized efficiently to Bohr sets, and also to allow for the fact that
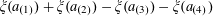 $\unicode[STIX]{x1D709}(a_{(1)})+\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}(a_{(3)})-\unicode[STIX]{x1D709}(a_{(4)})$
no longer vanishes, but instead has controlled word norm. This would require reworking of large portions of the standard additive combinatorics literature. We have thus elected instead to follow the second approach, also due to Gowers [Reference Gowers12], in which a certain probabilistic argument is used to “purify” a 1 percent additive map to a 99 percent additive map, albeit on a set that has no particular structure itself. To deal with this set we will use a more recent innovation, namely a variantFootnote
4
of the arithmetic regularity lemma [Reference Green13], [Reference Green and Tao18] to make the subsets of
$\unicode[STIX]{x1D709}(a_{(1)})+\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}(a_{(3)})-\unicode[STIX]{x1D709}(a_{(4)})$
no longer vanishes, but instead has controlled word norm. This would require reworking of large portions of the standard additive combinatorics literature. We have thus elected instead to follow the second approach, also due to Gowers [Reference Gowers12], in which a certain probabilistic argument is used to “purify” a 1 percent additive map to a 99 percent additive map, albeit on a set that has no particular structure itself. To deal with this set we will use a more recent innovation, namely a variantFootnote
4
of the arithmetic regularity lemma [Reference Green13], [Reference Green and Tao18] to make the subsets of
![]() $\mathbb{Z}/p\mathbb{Z}$
on which one has good control of
$\mathbb{Z}/p\mathbb{Z}$
on which one has good control of
![]() $\unicode[STIX]{x1D709}$
suitably “pseudorandom” in the sense of Gowers.
$\unicode[STIX]{x1D709}$
suitably “pseudorandom” in the sense of Gowers.
We turn to the details. We first locate a reasonably large quadruple of sets
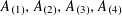 $A_{(1)},A_{(2)},A_{(3)},A_{(4)}$
on which
$A_{(1)},A_{(2)},A_{(3)},A_{(4)}$
on which
![]() $\unicode[STIX]{x1D709}$
is “almost a Freiman homomorphism” in the sense that most quadruples falling inside
$\unicode[STIX]{x1D709}$
is “almost a Freiman homomorphism” in the sense that most quadruples falling inside
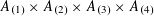 $A_{(1)}\times A_{(2)}\times A_{(3)}\times A_{(4)}$
are somewhat good. We call an additive quadruple
$A_{(1)}\times A_{(2)}\times A_{(3)}\times A_{(4)}$
are somewhat good. We call an additive quadruple
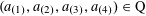 $(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in \operatorname{Q}$
very bad if
$(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in \operatorname{Q}$
very bad if
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}(a_{(1)})+\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}(a_{(3)})-\unicode[STIX]{x1D709}(a_{(4)})\Vert _{S}>\frac{1}{\unicode[STIX]{x1D70C}_{3}},\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}(a_{(1)})+\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}(a_{(3)})-\unicode[STIX]{x1D709}(a_{(4)})\Vert _{S}>\frac{1}{\unicode[STIX]{x1D70C}_{3}},\end{eqnarray}$$
and let
 $\operatorname{VBQ}\subset \operatorname{BQ}$
denote the space of all very bad additive quadruples.
$\operatorname{VBQ}\subset \operatorname{BQ}$
denote the space of all very bad additive quadruples.
Theorem 9.7. Let the notation and hypotheses be as in Theorem 8.1, and let
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D709}$
be as in Theorem 9.2. Let
$\unicode[STIX]{x1D709}$
be as in Theorem 9.2. Let
![]() $\vec{a}$
be the random additive quadruple from Corollary 9.5. Then there exist sets
$\vec{a}$
be the random additive quadruple from Corollary 9.5. Then there exist sets
 $A_{(1)},A_{(2)},A_{(3)},A_{(4)}\subset \unicode[STIX]{x1D6FA}$
such that
$A_{(1)},A_{(2)},A_{(3)},A_{(4)}\subset \unicode[STIX]{x1D6FA}$
such that
 $$\begin{eqnarray}\mathbb{E}W(\vec{a})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}W(\vec{a})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\end{eqnarray}$$
where
 $W:\text{Q}\rightarrow \mathbb{R}$
is the weight function
$W:\text{Q}\rightarrow \mathbb{R}$
is the weight function
 $$\begin{eqnarray}W(\vec{a}):=1_{A_{(1)}\times A_{(2)}\times A_{(3)}\times A_{(4)}}(\vec{\mathbf{a}})(1-\unicode[STIX]{x1D702}^{-C_{1}/100}1_{\operatorname{ VBQ}}(\vec{\mathbf{a}})).\end{eqnarray}$$
$$\begin{eqnarray}W(\vec{a}):=1_{A_{(1)}\times A_{(2)}\times A_{(3)}\times A_{(4)}}(\vec{\mathbf{a}})(1-\unicode[STIX]{x1D702}^{-C_{1}/100}1_{\operatorname{ VBQ}}(\vec{\mathbf{a}})).\end{eqnarray}$$
The idea here is that
![]() $W$
is a weight function that strongly penalizes very bad quadruples, and so Theorem 9.7 is asserting that “most” of the quadruples in
$W$
is a weight function that strongly penalizes very bad quadruples, and so Theorem 9.7 is asserting that “most” of the quadruples in
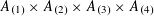 $A_{(1)}\times A_{(2)}\times A_{(3)}\times A_{(4)}$
are not very bad.
$A_{(1)}\times A_{(2)}\times A_{(3)}\times A_{(4)}$
are not very bad.
Proof. We will construct the sets
![]() $A_{(i)}$
by the probabilistic method, adapting an argument from [Reference Gowers12] in which the
$A_{(i)}$
by the probabilistic method, adapting an argument from [Reference Gowers12] in which the
![]() $A_{(i)}$
are created by applying a number of random linear “filters” to the graph of
$A_{(i)}$
are created by applying a number of random linear “filters” to the graph of
![]() $\unicode[STIX]{x1D709}$
to eliminate most of the additive quadruples that are not (almost) preserved by
$\unicode[STIX]{x1D709}$
to eliminate most of the additive quadruples that are not (almost) preserved by
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
We turn to the details. Let
![]() $m$
be the integer
$m$
be the integer
 $$\begin{eqnarray}m:=\biggl\lfloor\frac{\log \unicode[STIX]{x1D702}^{C_{1}}}{3\log 100}\biggr\rfloor.\end{eqnarray}$$
$$\begin{eqnarray}m:=\biggl\lfloor\frac{\log \unicode[STIX]{x1D702}^{C_{1}}}{3\log 100}\biggr\rfloor.\end{eqnarray}$$
We then select jointly independent random variables
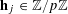 $\mathbf{h}_{j}\in \mathbb{Z}/p\mathbb{Z}$
and
$\mathbf{h}_{j}\in \mathbb{Z}/p\mathbb{Z}$
and
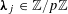 $\boldsymbol{\unicode[STIX]{x1D706}}_{j}\in \mathbb{Z}/p\mathbb{Z}$
for each for
$\boldsymbol{\unicode[STIX]{x1D706}}_{j}\in \mathbb{Z}/p\mathbb{Z}$
for each for
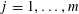 $j=1,\ldots ,m$
, by selecting each
$j=1,\ldots ,m$
, by selecting each
![]() $h_{j}$
regularly from
$h_{j}$
regularly from
 $B(S,\unicode[STIX]{x1D70C}_{2})$
, and selecting
$B(S,\unicode[STIX]{x1D70C}_{2})$
, and selecting
![]() $\boldsymbol{\unicode[STIX]{x1D706}}_{j}$
uniformly at random from
$\boldsymbol{\unicode[STIX]{x1D706}}_{j}$
uniformly at random from
![]() $\mathbb{Z}/p\mathbb{Z}$
; we also choose these random variables to be independent of
$\mathbb{Z}/p\mathbb{Z}$
; we also choose these random variables to be independent of
![]() $\vec{\mathbf{a}}$
. For
$\vec{\mathbf{a}}$
. For
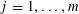 $j=1,\ldots ,m$
, we then let
$j=1,\ldots ,m$
, we then let
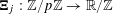 $\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{R}/\mathbb{Z}$
be the random map
$\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{R}/\mathbb{Z}$
be the random map
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(n):=\unicode[STIX]{x1D709}(n)\mathbf{h}_{j}+\frac{\boldsymbol{\unicode[STIX]{x1D706}}_{j}n}{p}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(n):=\unicode[STIX]{x1D709}(n)\mathbf{h}_{j}+\frac{\boldsymbol{\unicode[STIX]{x1D706}}_{j}n}{p}\end{eqnarray}$$
and then define the random sets
 $$\begin{eqnarray}\mathbf{A}_{(i)}:=\mathop{\bigcap }_{j=1}^{m}\mathbf{A}_{(i),j}\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{A}_{(i)}:=\mathop{\bigcap }_{j=1}^{m}\mathbf{A}_{(i),j}\end{eqnarray}$$
for
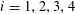 $i=1,2,3,4$
, where
$i=1,2,3,4$
, where
 $$\begin{eqnarray}\mathbf{A}_{(1),j}=\mathbf{A}_{(2),j}=\mathbf{A}_{(3),j}:=\{n\in \unicode[STIX]{x1D6FA}:\Vert \boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(n)\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant {\textstyle \frac{1}{200}}\}\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{A}_{(1),j}=\mathbf{A}_{(2),j}=\mathbf{A}_{(3),j}:=\{n\in \unicode[STIX]{x1D6FA}:\Vert \boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(n)\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant {\textstyle \frac{1}{200}}\}\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathbf{A}_{(4),j}:=\{n\in \unicode[STIX]{x1D6FA}:\Vert \boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(n)\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant {\textstyle \frac{1}{10}}\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{A}_{(4),j}:=\{n\in \unicode[STIX]{x1D6FA}:\Vert \boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(n)\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant {\textstyle \frac{1}{10}}\}.\end{eqnarray}$$
We will show that
 $$\begin{eqnarray}\mathbb{E}1_{A_{(1)}\times A_{(2)}\times A_{(3)}\times A_{(4)}}(\vec{\mathbf{a}})\gg \unicode[STIX]{x1D702}^{O(1)}100^{-3m}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}1_{A_{(1)}\times A_{(2)}\times A_{(3)}\times A_{(4)}}(\vec{\mathbf{a}})\gg \unicode[STIX]{x1D702}^{O(1)}100^{-3m}\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathbb{E}1_{A_{(1)}\times A_{(2)}\times A_{(3)}\times A_{(4)}}(\vec{\mathbf{a}})1_{\operatorname{BQ}}(\vec{a})\ll 2^{-m}\times 100^{-3m}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}1_{A_{(1)}\times A_{(2)}\times A_{(3)}\times A_{(4)}}(\vec{\mathbf{a}})1_{\operatorname{BQ}}(\vec{a})\ll 2^{-m}\times 100^{-3m}\end{eqnarray}$$
which will give the claim thanks to (9.13) and (9.12), if
![]() $C_{1}$
is large enough.
$C_{1}$
is large enough.
We first show (9.15). By Corollary 9.5 and linearity of expectation, it suffices to show that
 $$\begin{eqnarray}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i)}fori=1,2,3,4)\gg 100^{-3m}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i)}fori=1,2,3,4)\gg 100^{-3m}\end{eqnarray}$$
whenever
 $(a_{(1)},a_{(2)},a_{(3)},a_{(4)})$
lies in
$(a_{(1)},a_{(2)},a_{(3)},a_{(4)})$
lies in
 $\unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})$
. Actually, we will only show the weaker assertion that (9.17) holds for all but at most
$\unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})$
. Actually, we will only show the weaker assertion that (9.17) holds for all but at most
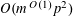 $O(m^{O(1)}p^{2})$
of the available additive quadruples
$O(m^{O(1)}p^{2})$
of the available additive quadruples
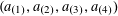 $(a_{(1)},a_{(2)},a_{(3)},a_{(4)})$
; this still suffices, since by (4.3), (9.1) each exceptional additive quadruple is attained with probability
$(a_{(1)},a_{(2)},a_{(3)},a_{(4)})$
; this still suffices, since by (4.3), (9.1) each exceptional additive quadruple is attained with probability
 $O(1/\unicode[STIX]{x1D70C}_{3}^{O(K)}p^{3})$
, and the additional factor of
$O(1/\unicode[STIX]{x1D70C}_{3}^{O(K)}p^{3})$
, and the additional factor of
![]() $p$
will dominate all the losses in
$p$
will dominate all the losses in
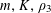 $m,K,\unicode[STIX]{x1D70C}_{3}$
thanks to (8.3), (9.13).
$m,K,\unicode[STIX]{x1D70C}_{3}$
thanks to (8.3), (9.13).
Fix an additive quadruple
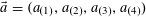 $\vec{a}=(a_{(1)},a_{(2)},a_{(3)},a_{(4)})$
in
$\vec{a}=(a_{(1)},a_{(2)},a_{(3)},a_{(4)})$
in
 $\unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})$
. The left-hand side of (9.17) factors as
$\unicode[STIX]{x1D6FA}^{4}\cap (\operatorname{Q}\backslash \operatorname{BQ})$
. The left-hand side of (9.17) factors as
 $$\begin{eqnarray}\mathop{\prod }_{j=1}^{m}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i)}\text{ for }i=1,2,3,4)\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{j=1}^{m}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i)}\text{ for }i=1,2,3,4)\end{eqnarray}$$
so it will suffice to show that for each
 $j=1,\ldots ,m$
, one has
$j=1,\ldots ,m$
, one has
 $$\begin{eqnarray}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i),j}\text{ for }i=1,2,3,4)\geqslant 100^{-3}-O\biggl(\frac{1}{m}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i),j}\text{ for }i=1,2,3,4)\geqslant 100^{-3}-O\biggl(\frac{1}{m}\biggr)\end{eqnarray}$$
for all but
 $O(m^{O(1)}p^{2})$
quadruples
$O(m^{O(1)}p^{2})$
quadruples
 $(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in \operatorname{Q}\backslash \operatorname{BQ}$
. Note however that from (9.14) we have
$(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in \operatorname{Q}\backslash \operatorname{BQ}$
. Note however that from (9.14) we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(1)})+\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(2)})-\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(3)})-\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(4)})\nonumber\\ \displaystyle & & \displaystyle \quad =(\unicode[STIX]{x1D709}(a_{(1)})+\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}(a_{(3)})-\unicode[STIX]{x1D709}(a_{(4)}))\mathbf{h}_{j}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(1)})+\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(2)})-\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(3)})-\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(4)})\nonumber\\ \displaystyle & & \displaystyle \quad =(\unicode[STIX]{x1D709}(a_{(1)})+\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}(a_{(3)})-\unicode[STIX]{x1D709}(a_{(4)}))\mathbf{h}_{j}\nonumber\end{eqnarray}$$
and hence by the hypothesis
 $(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in \operatorname{Q}\backslash \operatorname{BQ}$
and the range of
$(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in \operatorname{Q}\backslash \operatorname{BQ}$
and the range of
![]() $\mathbf{h}_{j}$
we have
$\mathbf{h}_{j}$
we have
 $$\begin{eqnarray}\biggl\|\frac{\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(1)})+\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(2)})-\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(3)})-\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(4)})}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \frac{1}{100}\end{eqnarray}$$
$$\begin{eqnarray}\biggl\|\frac{\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(1)})+\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(2)})-\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(3)})-\boldsymbol{\unicode[STIX]{x1D6EF}}_{\!j}(a_{(4)})}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \frac{1}{100}\end{eqnarray}$$
(for example). In particular, we see from the triangle inequality that the claim
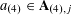 $a_{(4)}\in \mathbf{A}_{(4),j}$
is implied by the claims
$a_{(4)}\in \mathbf{A}_{(4),j}$
is implied by the claims
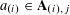 $a_{(i)}\in \mathbf{A}_{(i),j}$
for
$a_{(i)}\in \mathbf{A}_{(i),j}$
for
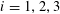 $i=1,2,3$
. Thus it suffices to show that
$i=1,2,3$
. Thus it suffices to show that
 $$\begin{eqnarray}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i),j}\text{ for }i=1,2,3)\geqslant 100^{-3}-O\biggl(\frac{1}{m}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i),j}\text{ for }i=1,2,3)\geqslant 100^{-3}-O\biggl(\frac{1}{m}\biggr)\end{eqnarray}$$
for all but
 $O(m^{O(1)}p^{2})$
triples
$O(m^{O(1)}p^{2})$
triples
 $(a_{(1)},a_{(2)},a_{(3)})\in (\mathbb{Z}/p\mathbb{Z})^{3}$
, noting that
$(a_{(1)},a_{(2)},a_{(3)})\in (\mathbb{Z}/p\mathbb{Z})^{3}$
, noting that
![]() $a_{(4)}$
is determined by
$a_{(4)}$
is determined by
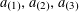 $a_{(1)},a_{(2)},a_{(3)}$
. We can write the left-hand side as
$a_{(1)},a_{(2)},a_{(3)}$
. We can write the left-hand side as
 $$\begin{eqnarray}\mathbb{P}\biggl(\frac{(\unicode[STIX]{x1D709}(a_{(1)}),\unicode[STIX]{x1D709}(a_{(2)}),\unicode[STIX]{x1D709}(a_{(3)}))\mathbf{h}_{j}+(a_{(1)},a_{(2)},a_{(3)})\boldsymbol{\unicode[STIX]{x1D706}}_{j}}{p}\in [-1/200,1/200]^{3}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}\biggl(\frac{(\unicode[STIX]{x1D709}(a_{(1)}),\unicode[STIX]{x1D709}(a_{(2)}),\unicode[STIX]{x1D709}(a_{(3)}))\mathbf{h}_{j}+(a_{(1)},a_{(2)},a_{(3)})\boldsymbol{\unicode[STIX]{x1D706}}_{j}}{p}\in [-1/200,1/200]^{3}\biggr),\end{eqnarray}$$
where we view the interval
 $[-1/200,1/200]$
as a subset of
$[-1/200,1/200]$
as a subset of
![]() $\mathbb{R}/\mathbb{Z}$
. Thus it will suffice to show the equidistribution property
$\mathbb{R}/\mathbb{Z}$
. Thus it will suffice to show the equidistribution property
 $$\begin{eqnarray}\inf _{x\in (\mathbb{R}/\mathbb{Z})^{3}}\mathbb{P}\biggl(\frac{(a_{(1)},a_{(2)},a_{(3)})\boldsymbol{\unicode[STIX]{x1D706}}_{j}}{p}\in x+[-1/200,1/200]^{3}\biggr)\geqslant 100^{-3}-O\biggl(\frac{1}{m}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\inf _{x\in (\mathbb{R}/\mathbb{Z})^{3}}\mathbb{P}\biggl(\frac{(a_{(1)},a_{(2)},a_{(3)})\boldsymbol{\unicode[STIX]{x1D706}}_{j}}{p}\in x+[-1/200,1/200]^{3}\biggr)\geqslant 100^{-3}-O\biggl(\frac{1}{m}\biggr).\end{eqnarray}$$
Let
 $\unicode[STIX]{x1D713}:(\mathbb{R}/\mathbb{Z})^{3}\rightarrow [0,1]$
be a Lipschitz cutoff supported on
$\unicode[STIX]{x1D713}:(\mathbb{R}/\mathbb{Z})^{3}\rightarrow [0,1]$
be a Lipschitz cutoff supported on
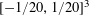 $[-1/20,1/20]^{3}$
that equals one on
$[-1/20,1/20]^{3}$
that equals one on
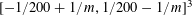 $[-1/200+1/m,1/200-1/m]^{3}$
and has Lipschitz constant
$[-1/200+1/m,1/200-1/m]^{3}$
and has Lipschitz constant
![]() $O(m)$
. Then we may lower bound the left-hand side by
$O(m)$
. Then we may lower bound the left-hand side by
 $$\begin{eqnarray}\inf _{x\in (\mathbb{R}/\mathbb{Z})^{3}}\mathbb{E}_{\unicode[STIX]{x1D706}\in \mathbb{Z}/p\mathbb{Z}}\unicode[STIX]{x1D713}\biggl(\frac{(a_{(1)},a_{(2)},a_{(3)})\unicode[STIX]{x1D706}}{p}-x\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\inf _{x\in (\mathbb{R}/\mathbb{Z})^{3}}\mathbb{E}_{\unicode[STIX]{x1D706}\in \mathbb{Z}/p\mathbb{Z}}\unicode[STIX]{x1D713}\biggl(\frac{(a_{(1)},a_{(2)},a_{(3)})\unicode[STIX]{x1D706}}{p}-x\biggr).\end{eqnarray}$$
By standard Fourier expansion (see e.g. [Reference Green and Tao17, Lemma A.9]), we may write
 $$\begin{eqnarray}\unicode[STIX]{x1D713}(y)=\mathop{\sum }_{k\in \mathbb{Z}^{3}:k=O(m^{O(1)})}c_{k}e(k\cdot y)+O\biggl(\frac{1}{m}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}(y)=\mathop{\sum }_{k\in \mathbb{Z}^{3}:k=O(m^{O(1)})}c_{k}e(k\cdot y)+O\biggl(\frac{1}{m}\biggr)\end{eqnarray}$$
for all
 $y\in (\mathbb{R}/\mathbb{Z})^{3}$
and some bounded Fourier coefficients
$y\in (\mathbb{R}/\mathbb{Z})^{3}$
and some bounded Fourier coefficients
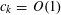 $c_{k}=O(1)$
; integrating in
$c_{k}=O(1)$
; integrating in
![]() $x$
, we see in particular that
$x$
, we see in particular that
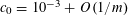 $c_{0}=10^{-3}+O(1/m)$
. We may thus write (9.19) as
$c_{0}=10^{-3}+O(1/m)$
. We may thus write (9.19) as
 $$\begin{eqnarray}10^{-3}+O\biggl(\frac{1}{m}\biggr)+O\biggl(\mathop{\sum }_{k\in \mathbb{Z}^{3}\backslash \{0\}:k=O(m^{O(1)})}|\mathbb{E}_{\unicode[STIX]{x1D706}\in \mathbb{Z}/p\mathbb{Z}}e_{p}(k\cdot (a_{(1)},a_{(2)},a_{(3)})\unicode[STIX]{x1D706})|\biggr)\end{eqnarray}$$
$$\begin{eqnarray}10^{-3}+O\biggl(\frac{1}{m}\biggr)+O\biggl(\mathop{\sum }_{k\in \mathbb{Z}^{3}\backslash \{0\}:k=O(m^{O(1)})}|\mathbb{E}_{\unicode[STIX]{x1D706}\in \mathbb{Z}/p\mathbb{Z}}e_{p}(k\cdot (a_{(1)},a_{(2)},a_{(3)})\unicode[STIX]{x1D706})|\biggr)\end{eqnarray}$$
which gives the desired claim as long as there are no relations of the form
 $$\begin{eqnarray}k\cdot (a_{(1)},a_{(2)},a_{(3)})=0\end{eqnarray}$$
$$\begin{eqnarray}k\cdot (a_{(1)},a_{(2)},a_{(3)})=0\end{eqnarray}$$
for some non-zero
![]() $k\in \mathbb{Z}^{3}$
with
$k\in \mathbb{Z}^{3}$
with
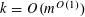 $k=O(m^{O(1)})$
. But it is easy to see that the number of
$k=O(m^{O(1)})$
. But it is easy to see that the number of
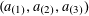 $(a_{(1)},a_{(2)},a_{(3)})$
with such a relation is
$(a_{(1)},a_{(2)},a_{(3)})$
with such a relation is
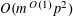 $O(m^{O(1)}p^{2})$
, thus concluding the proof of (9.15).
$O(m^{O(1)}p^{2})$
, thus concluding the proof of (9.15).
Now we show (9.16). By linearity of expectation as before, it suffices to show that
 $$\begin{eqnarray}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i)}\text{ for }i=1,2,3,4)\ll 2^{-m}\times 100^{-3m}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i)}\text{ for }i=1,2,3,4)\ll 2^{-m}\times 100^{-3m}\end{eqnarray}$$
for all but
 $O(m^{O(1)}p^{2})$
of the quadruples
$O(m^{O(1)}p^{2})$
of the quadruples
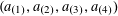 $(a_{(1)},a_{(2)},a_{(3)},a_{(4)})$
in
$(a_{(1)},a_{(2)},a_{(3)},a_{(4)})$
in
![]() $\operatorname{VBQ}$
. Using the factorization (9.18), it suffices to show that for each
$\operatorname{VBQ}$
. Using the factorization (9.18), it suffices to show that for each
 $j=1,\ldots ,m$
, one has
$j=1,\ldots ,m$
, one has
 $$\begin{eqnarray}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i),j}\text{ for }i=1,2,3,4)\leqslant 2^{-1}\times 100^{-3}+O\biggl(\frac{1}{m}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(a_{(i)}\in \mathbf{A}_{(i),j}\text{ for }i=1,2,3,4)\leqslant 2^{-1}\times 100^{-3}+O\biggl(\frac{1}{m}\biggr)\end{eqnarray}$$
for all but
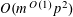 $O(m^{O(1)}p^{2})$
of the quadruples
$O(m^{O(1)}p^{2})$
of the quadruples
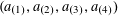 $(a_{(1)},a_{(2)},a_{(3)},a_{(4)})$
in
$(a_{(1)},a_{(2)},a_{(3)},a_{(4)})$
in
![]() $\operatorname{VBQ}$
.
$\operatorname{VBQ}$
.
The left-hand side may be written as
 $$\begin{eqnarray}\mathbb{P}\biggl(\frac{(\unicode[STIX]{x1D709}(a_{(1)}),\ldots ,\unicode[STIX]{x1D709}(a_{(4)}))\mathbf{h}_{j}}{p}+\vec{a}\boldsymbol{\unicode[STIX]{x1D706}}_{j}\in [-1/200,1/200]^{3}\times [-1/10,1/10]\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}\biggl(\frac{(\unicode[STIX]{x1D709}(a_{(1)}),\ldots ,\unicode[STIX]{x1D709}(a_{(4)}))\mathbf{h}_{j}}{p}+\vec{a}\boldsymbol{\unicode[STIX]{x1D706}}_{j}\in [-1/200,1/200]^{3}\times [-1/10,1/10]\biggr),\end{eqnarray}$$
which we bound above by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl((\unicode[STIX]{x1D709}(a_{(1)}),\unicode[STIX]{x1D709}(a_{(2)}),\unicode[STIX]{x1D709}(a_{(3)}))\mathbf{h}_{j}+(a_{(1)},a_{(2)},a_{(3)})\boldsymbol{\unicode[STIX]{x1D706}}_{j}\in [-1/200,1/200]^{3},\nonumber\\ \displaystyle & & \displaystyle \qquad \biggl\|\frac{\unicode[STIX]{x1D70E}\mathbf{h}_{j}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \frac{1}{8}\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl((\unicode[STIX]{x1D709}(a_{(1)}),\unicode[STIX]{x1D709}(a_{(2)}),\unicode[STIX]{x1D709}(a_{(3)}))\mathbf{h}_{j}+(a_{(1)},a_{(2)},a_{(3)})\boldsymbol{\unicode[STIX]{x1D706}}_{j}\in [-1/200,1/200]^{3},\nonumber\\ \displaystyle & & \displaystyle \qquad \biggl\|\frac{\unicode[STIX]{x1D70E}\mathbf{h}_{j}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \frac{1}{8}\biggr),\nonumber\end{eqnarray}$$
where
 $\unicode[STIX]{x1D70E}:=\unicode[STIX]{x1D709}(a_{(1)})+\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}(a_{(3)})-\unicode[STIX]{x1D709}(a_{(4)})$
. By arguing as in the proof of (9.15), we see that after deleting
$\unicode[STIX]{x1D70E}:=\unicode[STIX]{x1D709}(a_{(1)})+\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}(a_{(3)})-\unicode[STIX]{x1D709}(a_{(4)})$
. By arguing as in the proof of (9.15), we see that after deleting
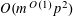 $O(m^{O(1)}p^{2})$
exceptional tuples, one has
$O(m^{O(1)}p^{2})$
exceptional tuples, one has
 $$\begin{eqnarray}\sup _{x\in (\mathbb{R}/\mathbb{Z})^{3}}\mathbb{P}((a_{(1)},a_{(2)},a_{(3)})\boldsymbol{\unicode[STIX]{x1D706}}_{j}\in x+[-1/200,1/200]^{3})\leqslant 100^{-3}+O\biggl(\frac{1}{m}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\sup _{x\in (\mathbb{R}/\mathbb{Z})^{3}}\mathbb{P}((a_{(1)},a_{(2)},a_{(3)})\boldsymbol{\unicode[STIX]{x1D706}}_{j}\in x+[-1/200,1/200]^{3})\leqslant 100^{-3}+O\biggl(\frac{1}{m}\biggr),\end{eqnarray}$$
so by Fubini’s theorem and the independence of
![]() $\mathbf{h}_{j}$
and
$\mathbf{h}_{j}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D706}}_{j}$
it will suffice to show that
$\boldsymbol{\unicode[STIX]{x1D706}}_{j}$
it will suffice to show that
 $$\begin{eqnarray}\mathbb{P}\biggl(\biggl\|\frac{\unicode[STIX]{x1D70E}\mathbf{h}_{j}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \frac{1}{8}\biggr)\leqslant 2^{-1}+O\biggl(\frac{1}{m}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}\biggl(\biggl\|\frac{\unicode[STIX]{x1D70E}\mathbf{h}_{j}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \frac{1}{8}\biggr)\leqslant 2^{-1}+O\biggl(\frac{1}{m}\biggr).\end{eqnarray}$$
However, by Lemma 4.6 and the hypothesis
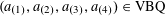 $(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in \operatorname{VBQ}$
we may find
$(a_{(1)},a_{(2)},a_{(3)},a_{(4)})\in \operatorname{VBQ}$
we may find
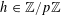 $h\in \mathbb{Z}/p\mathbb{Z}$
such that
$h\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\biggl\|\frac{\unicode[STIX]{x1D70E}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}>K^{-O(1)}\Vert h\Vert _{S^{\bot }}\unicode[STIX]{x1D70C}_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl\|\frac{\unicode[STIX]{x1D70E}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}>K^{-O(1)}\Vert h\Vert _{S^{\bot }}\unicode[STIX]{x1D70C}_{3}.\end{eqnarray}$$
In particular,
![]() $h$
is non-zero. By repeatedly doubling
$h$
is non-zero. By repeatedly doubling
![]() $h$
until
$h$
until
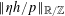 $\Vert \unicode[STIX]{x1D702}h/p\Vert _{\mathbb{R}/\mathbb{Z}}$
exceeds
$\Vert \unicode[STIX]{x1D702}h/p\Vert _{\mathbb{R}/\mathbb{Z}}$
exceeds
![]() ${\textstyle \frac{1}{4}}$
, we may also assume that
${\textstyle \frac{1}{4}}$
, we may also assume that
 $$\begin{eqnarray}\frac{1}{2}\geqslant \biggl\|\frac{\unicode[STIX]{x1D702}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}>\frac{1}{4}\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{2}\geqslant \biggl\|\frac{\unicode[STIX]{x1D702}h}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}>\frac{1}{4}\end{eqnarray}$$
and thus
 $$\begin{eqnarray}\Vert h\Vert _{S^{\bot }}\ll K^{O(1)}\unicode[STIX]{x1D70C}_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert h\Vert _{S^{\bot }}\ll K^{O(1)}\unicode[STIX]{x1D70C}_{3}.\end{eqnarray}$$
From Lemma 4.4 we conclude that
 $$\begin{eqnarray}\mathbb{P}\biggl(\biggl\|\frac{\unicode[STIX]{x1D702}(\mathbf{h}_{j}+h)}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \frac{1}{8}\biggr)=\mathbb{P}\biggl(\biggl\|\frac{\unicode[STIX]{x1D702}\mathbf{h}_{j}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \frac{1}{8}\biggr)+O\biggl(\frac{1}{m}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}\biggl(\biggl\|\frac{\unicode[STIX]{x1D702}(\mathbf{h}_{j}+h)}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \frac{1}{8}\biggr)=\mathbb{P}\biggl(\biggl\|\frac{\unicode[STIX]{x1D702}\mathbf{h}_{j}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \frac{1}{8}\biggr)+O\biggl(\frac{1}{m}\biggr).\end{eqnarray}$$
But from the triangle inequality we see that the events
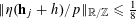 $\Vert \unicode[STIX]{x1D702}(\mathbf{h}_{j}+h)/p\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant {\textstyle \frac{1}{8}}$
,
$\Vert \unicode[STIX]{x1D702}(\mathbf{h}_{j}+h)/p\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant {\textstyle \frac{1}{8}}$
,
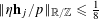 $\Vert \unicode[STIX]{x1D702}\mathbf{h}_{j}/p\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant {\textstyle \frac{1}{8}}$
are disjoint. The claim follows.◻
$\Vert \unicode[STIX]{x1D702}\mathbf{h}_{j}/p\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant {\textstyle \frac{1}{8}}$
are disjoint. The claim follows.◻
9.8 Fourth step: the rough set is pseudorandom in a Bohr set
The sets
![]() $A_{(i)}$
provided by Theorem 9.7 are currently rather arbitrary. In particular we have no control on the pseudorandomness of these sets (as measured by local Gowers
$A_{(i)}$
provided by Theorem 9.7 are currently rather arbitrary. In particular we have no control on the pseudorandomness of these sets (as measured by local Gowers
![]() $U^{2}$
norms) in the Bohr sets we are working with. However, it is possible to use an “energy decrement argument” to pass to smallerFootnote
5
Bohr sets in which the sets
$U^{2}$
norms) in the Bohr sets we are working with. However, it is possible to use an “energy decrement argument” to pass to smallerFootnote
5
Bohr sets in which the sets
![]() $A_{(i)}$
do enjoy good pseudorandomness properties, basically by converting any large Fourier coefficient of any of the
$A_{(i)}$
do enjoy good pseudorandomness properties, basically by converting any large Fourier coefficient of any of the
![]() $A_{(i)}$
in a Bohr set into a refinement of the Bohr sets (which add the frequency of the large Fourier coefficient to the frequency set
$A_{(i)}$
in a Bohr set into a refinement of the Bohr sets (which add the frequency of the large Fourier coefficient to the frequency set
![]() $S$
) on which the indicator function
$S$
) on which the indicator function
![]() $1_{A_{(i)}}$
has smaller variance. Furthermore, it is possible to shrink the Bohr sets in this fashion without destroying the conclusion (9.11) of Theorem 9.7.
$1_{A_{(i)}}$
has smaller variance. Furthermore, it is possible to shrink the Bohr sets in this fashion without destroying the conclusion (9.11) of Theorem 9.7.
Here is a precise statement.
Theorem 9.9. Let the notation and hypotheses be as in Theorem 8.1, and let
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D709}$
be as in Theorem 9.2. Let
$\unicode[STIX]{x1D709}$
be as in Theorem 9.2. Let
 $A_{(1)},A_{(2)},A_{(3)},A_{(4)},W$
be as in Theorem 9.7. Then there exists a natural number
$A_{(1)},A_{(2)},A_{(3)},A_{(4)},W$
be as in Theorem 9.7. Then there exists a natural number
![]() $j$
,
$j$
,
 $j\leqslant \unicode[STIX]{x1D702}^{-10^{3}C_{1}}$
, an additive quadruple
$j\leqslant \unicode[STIX]{x1D702}^{-10^{3}C_{1}}$
, an additive quadruple
 $\vec{a}_{1}=(a_{(1),1},a_{(2),1},a_{(3),1},a_{(4),1})\in \operatorname{Q}$
, and a set
$\vec{a}_{1}=(a_{(1),1},a_{(2),1},a_{(3),1},a_{(4),1})\in \operatorname{Q}$
, and a set
![]() $S_{1}$
,
$S_{1}$
,
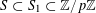 $S\subset S_{1}\subset \mathbb{Z}/p\mathbb{Z}$
with
$S\subset S_{1}\subset \mathbb{Z}/p\mathbb{Z}$
with
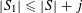 $|S_{1}|\leqslant |S|+j$
, with the following properties.
$|S_{1}|\leqslant |S|+j$
, with the following properties.
-
(i) (Few very bad quadruples) We have
(9.20)where $$\begin{eqnarray}\mathbb{E}W(\vec{\mathbf{a}})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}W(\vec{\mathbf{a}})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\end{eqnarray}$$
 $\vec{\mathbf{a}}$
is a random additive quadruple centred at
$\vec{\mathbf{a}}$
is a random additive quadruple centred at
 $\vec{a}_{1}$
with frequencies
$\vec{a}_{1}$
with frequencies
 $S_{1}$
and scales
$S_{1}$
and scales
 $\unicode[STIX]{x1D70C}_{2,j+2}$
,
$\unicode[STIX]{x1D70C}_{2,j+2}$
,
 $\unicode[STIX]{x1D70C}_{2,j+1}$
, and
$\unicode[STIX]{x1D70C}_{2,j+1}$
, and
 $\unicode[STIX]{x1D70C}_{2,j}$
.
$\unicode[STIX]{x1D70C}_{2,j}$
.
-
(ii) (Local Fourier pseudorandomness) For each
 $i=1,2,3,4$
, we have where
$i=1,2,3,4$
, we have where $$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1})f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\leqslant \unicode[STIX]{x1D702}^{100C_{1}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\mathbb{E}f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1})f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|\leqslant \unicode[STIX]{x1D702}^{100C_{1}},\nonumber\end{eqnarray}$$
 $f_{i}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
denotes the balanced function (9.21)
$f_{i}:\mathbb{Z}/p\mathbb{Z}\rightarrow [-1,1]$
denotes the balanced function (9.21) $$\begin{eqnarray}f_{i}(a_{(i)}):=1_{A_{(i)}}(a_{(i)})-\unicode[STIX]{x1D6FC}_{i},\end{eqnarray}$$
$$\begin{eqnarray}f_{i}(a_{(i)}):=1_{A_{(i)}}(a_{(i)})-\unicode[STIX]{x1D6FC}_{i},\end{eqnarray}$$
 $\unicode[STIX]{x1D6FC}_{i}$
denotes the mean (9.22)and where
$\unicode[STIX]{x1D6FC}_{i}$
denotes the mean (9.22)and where $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i}:=\mathbb{E}1_{A_{(i)}}(\mathbf{a}_{(i)}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i}:=\mathbb{E}1_{A_{(i)}}(\mathbf{a}_{(i)}),\end{eqnarray}$$
 $\mathbf{a}_{(i)}$
and
$\mathbf{a}_{(i)}$
and
 $\mathbf{h}_{0},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1},\mathbf{h}_{1}^{\prime }$
are drawn independently and regularly from the Bohr sets
$\mathbf{h}_{0},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1},\mathbf{h}_{1}^{\prime }$
are drawn independently and regularly from the Bohr sets
 $a_{(i),1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j+l_{i}})$
and
$a_{(i),1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j+l_{i}})$
and
 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+10})$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+10})$
,
 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+10})$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+10})$
,
 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+11})$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+11})$
,
 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+11})$
respectively, with the quantity
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+11})$
respectively, with the quantity
 $l_{i}$
given by (9.9).
$l_{i}$
given by (9.9).
Proof. We will formulate the “energy decrement” argument here as a “score maximization” argument. Define a
![]() $4$
-neighbourhood to be a tuple
$4$
-neighbourhood to be a tuple
 $$\begin{eqnarray}N=(\vec{a}_{1},j,S_{1}),\end{eqnarray}$$
$$\begin{eqnarray}N=(\vec{a}_{1},j,S_{1}),\end{eqnarray}$$
where
![]() $\vec{a}_{1}\in \text{Q}$
is an additive quadruple,
$\vec{a}_{1}\in \text{Q}$
is an additive quadruple,
![]() $j$
is a natural number between
$j$
is a natural number between
![]() $0$
and
$0$
and
![]() $\unicode[STIX]{x1D702}^{-10^{3}C_{1}}$
, and
$\unicode[STIX]{x1D702}^{-10^{3}C_{1}}$
, and
![]() $S_{1}$
is a subset of
$S_{1}$
is a subset of
![]() $\mathbb{Z}/p\mathbb{Z}$
containing
$\mathbb{Z}/p\mathbb{Z}$
containing
![]() $S$
with
$S$
with
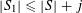 $|S_{1}|\leqslant |S|+j$
; we refer to
$|S_{1}|\leqslant |S|+j$
; we refer to
![]() $j$
as the depth of the
$j$
as the depth of the
![]() $4$
-neighbourhood
$4$
-neighbourhood
![]() $N$
. Given such a neighbourhood, we define the score
$N$
. Given such a neighbourhood, we define the score
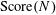 $\operatorname{Score}(N)$
of the
$\operatorname{Score}(N)$
of the
![]() $4$
-neighbourhood to be the quantity
$4$
-neighbourhood to be the quantity
 $$\begin{eqnarray}\operatorname{Score}(N):=\mathbb{E}W(\vec{\mathbf{a}})-\unicode[STIX]{x1D702}^{2C_{1}}\mathop{\sum }_{i=1}^{4}\text{E}_{i}(N)-\unicode[STIX]{x1D702}^{10^{3}C_{1}}j,\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Score}(N):=\mathbb{E}W(\vec{\mathbf{a}})-\unicode[STIX]{x1D702}^{2C_{1}}\mathop{\sum }_{i=1}^{4}\text{E}_{i}(N)-\unicode[STIX]{x1D702}^{10^{3}C_{1}}j,\end{eqnarray}$$
where
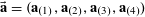 $\vec{\mathbf{a}}=(\mathbf{a}_{(1)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)})$
is a random additive quadruple centred at
$\vec{\mathbf{a}}=(\mathbf{a}_{(1)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)})$
is a random additive quadruple centred at
![]() $\vec{a}_{1}$
with frequencies
$\vec{a}_{1}$
with frequencies
![]() $S_{1}$
and scales
$S_{1}$
and scales
 $\unicode[STIX]{x1D70C}_{2,j+2},\unicode[STIX]{x1D70C}_{2,j+1},\unicode[STIX]{x1D70C}_{2,j}$
, and
$\unicode[STIX]{x1D70C}_{2,j+2},\unicode[STIX]{x1D70C}_{2,j+1},\unicode[STIX]{x1D70C}_{2,j}$
, and
![]() $\operatorname{E}_{i}$
is the energy-type quantity
$\operatorname{E}_{i}$
is the energy-type quantity
 $$\begin{eqnarray}\operatorname{E}_{i}(N):=\operatorname{Var}1_{A_{(i)}}(\mathbf{a}_{(i)}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{E}_{i}(N):=\operatorname{Var}1_{A_{(i)}}(\mathbf{a}_{(i)}).\end{eqnarray}$$
If we define
![]() $N_{0}$
to be the
$N_{0}$
to be the
![]() $4$
-neighbourhood
$4$
-neighbourhood
 $$\begin{eqnarray}N_{0}:=(\vec{a}_{0},0,S),\end{eqnarray}$$
$$\begin{eqnarray}N_{0}:=(\vec{a}_{0},0,S),\end{eqnarray}$$
then Theorem 9.7 tells us that
 $$\begin{eqnarray}\operatorname{Score}(N_{0})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Score}(N_{0})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
We choose
 $$\begin{eqnarray}N:=(\vec{a}_{1},j,S_{1})\end{eqnarray}$$
$$\begin{eqnarray}N:=(\vec{a}_{1},j,S_{1})\end{eqnarray}$$
to be a
![]() $4$
-neighbourhood that comes within
$4$
-neighbourhood that comes within
![]() $\unicode[STIX]{x1D702}^{10^{3}C_{1}}$
(for example) of maximizing the adjusted score. Then we must have
$\unicode[STIX]{x1D702}^{10^{3}C_{1}}$
(for example) of maximizing the adjusted score. Then we must have
 $$\begin{eqnarray}\operatorname{Score}(N)\geqslant \operatorname{Score}(N_{0})-\unicode[STIX]{x1D702}^{10^{3}C_{1}}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Score}(N)\geqslant \operatorname{Score}(N_{0})-\unicode[STIX]{x1D702}^{10^{3}C_{1}}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\end{eqnarray}$$
which from (9.23) implies the bound (9.20), as well as the bound
 $$\begin{eqnarray}j\leqslant \unicode[STIX]{x1D702}^{-10^{3}C_{1}}-10^{3}\end{eqnarray}$$
$$\begin{eqnarray}j\leqslant \unicode[STIX]{x1D702}^{-10^{3}C_{1}}-10^{3}\end{eqnarray}$$
(for example). It will then suffice to show that property (ii) of the theorem holds.
It remains to show (ii). Let
 $i=1,2,3,4$
, and write
$i=1,2,3,4$
, and write
 $$\begin{eqnarray}\vec{a}_{1}=(a_{(1),1},a_{(2),1},a_{(3),1},a_{(4),1}).\end{eqnarray}$$
$$\begin{eqnarray}\vec{a}_{1}=(a_{(1),1},a_{(2),1},a_{(3),1},a_{(4),1}).\end{eqnarray}$$
Suppose for contradiction that
 $$\begin{eqnarray}|\mathbb{E}f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1})f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|>\unicode[STIX]{x1D702}^{100C_{1}},\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1})f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{i}(\mathbf{a}_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })|>\unicode[STIX]{x1D702}^{100C_{1}},\end{eqnarray}$$
where
![]() $f_{i}$
is given by (9.21), and
$f_{i}$
is given by (9.21), and
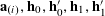 $\mathbf{a}_{(i)},\mathbf{h}_{0},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1},\mathbf{h}_{1}^{\prime }$
are drawn independently and regularly from the Bohr sets
$\mathbf{a}_{(i)},\mathbf{h}_{0},\mathbf{h}_{0}^{\prime },\mathbf{h}_{1},\mathbf{h}_{1}^{\prime }$
are drawn independently and regularly from the Bohr sets
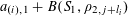 $a_{(i),1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j+l_{i}})$
,
$a_{(i),1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j+l_{i}})$
,
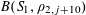 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+10})$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+10})$
,
 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+10})$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+10})$
,
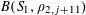 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+11})$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+11})$
,
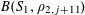 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+11})$
, with
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+11})$
, with
![]() $l_{i}$
given by (9.9).
$l_{i}$
given by (9.9).
We will use (9.26) to construct a random
![]() $4$
-neighbourhood
$4$
-neighbourhood
![]() $\mathbf{N}$
of depth
$\mathbf{N}$
of depth
![]() $j+20$
obeying the estimates
$j+20$
obeying the estimates
 $$\begin{eqnarray}\mathbb{E}W(\mathbf{N})=W(N)+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}})\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}W(\mathbf{N})=W(N)+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}})\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathbb{E}\operatorname{E}_{i^{\prime }}(\mathbf{N})\leqslant \operatorname{E}_{i^{\prime }}(N)-\unicode[STIX]{x1D702}^{500C_{1}}1_{i=i^{\prime }}+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}})\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}\operatorname{E}_{i^{\prime }}(\mathbf{N})\leqslant \operatorname{E}_{i^{\prime }}(N)-\unicode[STIX]{x1D702}^{500C_{1}}1_{i=i^{\prime }}+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}})\end{eqnarray}$$
for
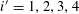 $i^{\prime }=1,2,3,4$
. If we have the estimates (9.27), (9.28), we conclude from (9.23) and linearity of expectation that
$i^{\prime }=1,2,3,4$
. If we have the estimates (9.27), (9.28), we conclude from (9.23) and linearity of expectation that
 $$\begin{eqnarray}\mathbb{E}\operatorname{Score}(\mathbf{N})>\operatorname{Score}(N)+\unicode[STIX]{x1D702}^{600C_{1}},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}\operatorname{Score}(\mathbf{N})>\operatorname{Score}(N)+\unicode[STIX]{x1D702}^{600C_{1}},\end{eqnarray}$$
contradicting the near-maximality of
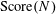 $\operatorname{Score}(N)$
.
$\operatorname{Score}(N)$
.
It remains to construct
![]() $\mathbf{N}$
obeying (9.27), (9.28). We begin by noting that for each
$\mathbf{N}$
obeying (9.27), (9.28). We begin by noting that for each
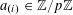 $a_{(i)}\in \mathbb{Z}/p\mathbb{Z}$
, the Gowers uniformity-type quantity
$a_{(i)}\in \mathbb{Z}/p\mathbb{Z}$
, the Gowers uniformity-type quantity
 $$\begin{eqnarray}\mathbb{E}f_{i}(a_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1})f_{i}(a_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })f_{i}(a_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{i}(a_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f_{i}(a_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1})f_{i}(a_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })f_{i}(a_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{i}(a_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })\end{eqnarray}$$
can be factored as
 $$\begin{eqnarray}\mathop{\sum }_{h_{0},h_{0}^{\prime }}\mathbb{P}(\mathbf{h}_{0}=h_{0},\mathbf{h}_{0}^{\prime }=h_{0}^{\prime })|\mathbb{E}f_{i}(a_{(i)}+h_{0}+\mathbf{h}_{1})f_{i}(a_{(i)}+h_{0}^{\prime }+\mathbf{h}_{1})|^{2}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{h_{0},h_{0}^{\prime }}\mathbb{P}(\mathbf{h}_{0}=h_{0},\mathbf{h}_{0}^{\prime }=h_{0}^{\prime })|\mathbb{E}f_{i}(a_{(i)}+h_{0}+\mathbf{h}_{1})f_{i}(a_{(i)}+h_{0}^{\prime }+\mathbf{h}_{1})|^{2}\end{eqnarray}$$
and thus takes values between
![]() $0$
and
$0$
and
![]() $1$
. By (9.26) and Lemma 2.2, we may thus find a set
$1$
. By (9.26) and Lemma 2.2, we may thus find a set
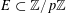 $E\subset \mathbb{Z}/p\mathbb{Z}$
with
$E\subset \mathbb{Z}/p\mathbb{Z}$
with
 $$\begin{eqnarray}\mathbb{P}(\mathbf{a}_{(i)}\in E)\gg \unicode[STIX]{x1D702}^{100C_{1}}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{a}_{(i)}\in E)\gg \unicode[STIX]{x1D702}^{100C_{1}}\end{eqnarray}$$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}f_{i}(a_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1})f_{i}(a_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })f_{i}(a_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{i}(a_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{100C_{1}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}f_{i}(a_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1})f_{i}(a_{(i)}+\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })f_{i}(a_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1})f_{i}(a_{(i)}+\mathbf{h}_{0}^{\prime }+\mathbf{h}_{1}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{100C_{1}}\nonumber\end{eqnarray}$$
for all
![]() $a_{(i)}\in E$
. Applying Theorem 4.12, we may thus find, for each
$a_{(i)}\in E$
. Applying Theorem 4.12, we may thus find, for each
![]() $a_{(i)}\in E$
, a frequency
$a_{(i)}\in E$
, a frequency
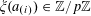 $\unicode[STIX]{x1D709}(a_{(i)})\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}(a_{(i)})\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})\mathbb{E}|\mathbb{E}f_{i}(a_{(i)}+n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(a_{(i)})\mathbf{n}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{100C_{1}},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})\mathbb{E}|\mathbb{E}f_{i}(a_{(i)}+n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(a_{(i)})\mathbf{n}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{100C_{1}},\end{eqnarray}$$
where
![]() $\mathbf{n}_{0},\mathbf{n}_{1}$
are drawn independently and regularly from
$\mathbf{n}_{0},\mathbf{n}_{1}$
are drawn independently and regularly from
 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+10})$
and
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+10})$
and
 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+11})$
respectively, independently of the
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+11})$
respectively, independently of the
![]() $\mathbf{a}_{(i)}$
.
$\mathbf{a}_{(i)}$
.
If we define
![]() $\unicode[STIX]{x1D709}(a_{(i)})$
arbitrarily for
$\unicode[STIX]{x1D709}(a_{(i)})$
arbitrarily for
![]() $a_{(i)}\not \in E$
(e.g. setting
$a_{(i)}\not \in E$
(e.g. setting
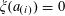 $\unicode[STIX]{x1D709}(a_{(i)})=0$
), we thus have
$\unicode[STIX]{x1D709}(a_{(i)})=0$
), we thus have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},a_{(i)}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{a}_{(i)}=a_{(i)})\mathbb{E}|\mathbb{E}(f_{i}(a_{(i)}+n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(a_{(i)})\mathbf{n}_{1}))|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{200C_{1}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},a_{(i)}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{a}_{(i)}=a_{(i)})\mathbb{E}|\mathbb{E}(f_{i}(a_{(i)}+n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(a_{(i)})\mathbf{n}_{1}))|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{200C_{1}}.\nonumber\end{eqnarray}$$
In particular, there exists a
![]() $1$
-bounded function
$1$
-bounded function
 $g:\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
such that
$g:\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
such that
 $$\begin{eqnarray}|\mathbb{E}g(\mathbf{n}_{0},\mathbf{a}_{(i)})f_{i}(\mathbf{a}_{(i)}+\mathbf{n}_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}^{200C_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}g(\mathbf{n}_{0},\mathbf{a}_{(i)})f_{i}(\mathbf{a}_{(i)}+\mathbf{n}_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}^{200C_{1}}.\end{eqnarray}$$
We now construct the random
![]() $4$
-neighbourhood
$4$
-neighbourhood
![]() $\mathbf{N}$
as follows. We first construct a random additive quadruple
$\mathbf{N}$
as follows. We first construct a random additive quadruple
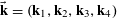 $\vec{\mathbf{k}}=(\mathbf{k}_{1},\mathbf{k}_{2},\mathbf{k}_{3},\mathbf{k}_{4})$
centred at the origin
$\vec{\mathbf{k}}=(\mathbf{k}_{1},\mathbf{k}_{2},\mathbf{k}_{3},\mathbf{k}_{4})$
centred at the origin
 $(0,0,0,0)$
with frequency set
$(0,0,0,0)$
with frequency set
![]() $S_{1}$
and scales
$S_{1}$
and scales
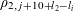 $\unicode[STIX]{x1D70C}_{2,j+10+l_{2}-l_{i}}$
,
$\unicode[STIX]{x1D70C}_{2,j+10+l_{2}-l_{i}}$
,
 $\unicode[STIX]{x1D70C}_{2,j+10+l_{3}-l_{i}}$
,
$\unicode[STIX]{x1D70C}_{2,j+10+l_{3}-l_{i}}$
,
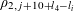 $\unicode[STIX]{x1D70C}_{2,j+10+l_{4}-l_{i}}$
, and independent of all previous random variables. We then set
$\unicode[STIX]{x1D70C}_{2,j+10+l_{4}-l_{i}}$
, and independent of all previous random variables. We then set
 $$\begin{eqnarray}\mathbf{N}:=(\vec{\mathbf{a}}+\vec{\mathbf{k}},j+20,S_{1}\cup \{\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{N}:=(\vec{\mathbf{a}}+\vec{\mathbf{k}},j+20,S_{1}\cup \{\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\}).\end{eqnarray}$$
It is easy to verify that
![]() $\mathbf{N}$
is a (random)
$\mathbf{N}$
is a (random)
![]() $4$
-neighbourhood.
$4$
-neighbourhood.
We now verify (9.27). The left-hand side of (9.27) can be expanded as
 $$\begin{eqnarray}\mathbb{E}W(\vec{\mathbf{a}}+\vec{\mathbf{k}}+\vec{\mathbf{h}}),\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}W(\vec{\mathbf{a}}+\vec{\mathbf{k}}+\vec{\mathbf{h}}),\end{eqnarray}$$
where, once
![]() $\vec{\mathbf{a}}$
and
$\vec{\mathbf{a}}$
and
![]() $\vec{\mathbf{k}}$
are chosen, the random additive quadruple
$\vec{\mathbf{k}}$
are chosen, the random additive quadruple
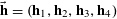 $\vec{\mathbf{h}}=(\mathbf{h}_{1},\mathbf{h}_{2},\mathbf{h}_{3},\mathbf{h}_{4})$
is selected to be centred at
$\vec{\mathbf{h}}=(\mathbf{h}_{1},\mathbf{h}_{2},\mathbf{h}_{3},\mathbf{h}_{4})$
is selected to be centred at
 $(0,0,0,0)$
with frequencies
$(0,0,0,0)$
with frequencies
 $S_{1}\cup \{\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\}$
and scales
$S_{1}\cup \{\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\}$
and scales
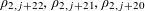 $\unicode[STIX]{x1D70C}_{2,j+22},\unicode[STIX]{x1D70C}_{2,j+21},\unicode[STIX]{x1D70C}_{2,j+20}$
.
$\unicode[STIX]{x1D70C}_{2,j+22},\unicode[STIX]{x1D70C}_{2,j+21},\unicode[STIX]{x1D70C}_{2,j+20}$
.
From two applications of Lemma 4.4 (and the fact that
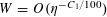 $W=O(\unicode[STIX]{x1D702}^{-C_{1}/100})$
), we have
$W=O(\unicode[STIX]{x1D702}^{-C_{1}/100})$
), we have
 $$\begin{eqnarray}\mathbb{E}W(\vec{\mathbf{a}}+\vec{\mathbf{k}}+\vec{\mathbf{h}})=\mathbb{E}W(\vec{\mathbf{a}}+\vec{\mathbf{k}})+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}})=\mathbb{E}W(\vec{\mathbf{a}})+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}})\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}W(\vec{\mathbf{a}}+\vec{\mathbf{k}}+\vec{\mathbf{h}})=\mathbb{E}W(\vec{\mathbf{a}}+\vec{\mathbf{k}})+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}})=\mathbb{E}W(\vec{\mathbf{a}})+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}})\end{eqnarray}$$
(for example). The claim (9.27) now follows from (9.23).
Now we verify (9.28). By (9.24), we have
 $$\begin{eqnarray}\operatorname{E}_{i^{\prime }}(\mathbf{N})=\mathop{\sum }_{\vec{a},\vec{k}}\mathbb{P}(\vec{\mathbf{a}}=\vec{a},\vec{\mathbf{k}}=\vec{k})\mathbb{E}|1_{A_{(i^{\prime })}}(a_{(i^{\prime })}+k_{i^{\prime }}+\mathbf{h}_{i^{\prime }})-\unicode[STIX]{x1D6FC}_{i^{\prime },\vec{a},\vec{k}}|^{2},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{E}_{i^{\prime }}(\mathbf{N})=\mathop{\sum }_{\vec{a},\vec{k}}\mathbb{P}(\vec{\mathbf{a}}=\vec{a},\vec{\mathbf{k}}=\vec{k})\mathbb{E}|1_{A_{(i^{\prime })}}(a_{(i^{\prime })}+k_{i^{\prime }}+\mathbf{h}_{i^{\prime }})-\unicode[STIX]{x1D6FC}_{i^{\prime },\vec{a},\vec{k}}|^{2},\end{eqnarray}$$
where
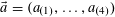 $\vec{a}=(a_{(1)},\ldots ,a_{(4)})$
,
$\vec{a}=(a_{(1)},\ldots ,a_{(4)})$
,
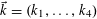 $\vec{k}=(k_{1},\ldots ,k_{4})$
, and
$\vec{k}=(k_{1},\ldots ,k_{4})$
, and
![]() $\unicode[STIX]{x1D6FC}_{i^{\prime },\vec{a},\vec{k}}$
is the quantity
$\unicode[STIX]{x1D6FC}_{i^{\prime },\vec{a},\vec{k}}$
is the quantity
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i^{\prime },\vec{a},\vec{k}}:=\mathbb{E}1_{A_{(i^{\prime })}}(a_{(i^{\prime })}+k_{i^{\prime }}+\mathbf{h}_{i^{\prime }}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i^{\prime },\vec{a},\vec{k}}:=\mathbb{E}1_{A_{(i^{\prime })}}(a_{(i^{\prime })}+k_{i^{\prime }}+\mathbf{h}_{i^{\prime }}).\end{eqnarray}$$
By Pythagoras’ theorem, we thus have
 $$\begin{eqnarray}\operatorname{E}_{i^{\prime }}(\mathbf{N})=\mathop{\sum }_{\vec{a},\vec{k}}\mathbb{P}(\vec{\mathbf{a}}=\vec{a},\vec{\mathbf{k}}=\vec{k})\mathbb{E}|1_{A_{(i^{\prime })}}(a_{(i^{\prime })}+k_{i^{\prime }}+\mathbf{h}_{i^{\prime }})-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2}-|\unicode[STIX]{x1D6FC}_{i^{\prime },\vec{a},\vec{k}}-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{E}_{i^{\prime }}(\mathbf{N})=\mathop{\sum }_{\vec{a},\vec{k}}\mathbb{P}(\vec{\mathbf{a}}=\vec{a},\vec{\mathbf{k}}=\vec{k})\mathbb{E}|1_{A_{(i^{\prime })}}(a_{(i^{\prime })}+k_{i^{\prime }}+\mathbf{h}_{i^{\prime }})-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2}-|\unicode[STIX]{x1D6FC}_{i^{\prime },\vec{a},\vec{k}}-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FC}_{i^{\prime }}$
is defined in (9.22). We shall shortly establish the bound
$\unicode[STIX]{x1D6FC}_{i^{\prime }}$
is defined in (9.22). We shall shortly establish the bound
 $$\begin{eqnarray}|\unicode[STIX]{x1D6FC}_{i^{\prime },\vec{a},\vec{k}}-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2}\gg \unicode[STIX]{x1D702}^{400C_{1}}1_{i^{\prime }=i}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6FC}_{i^{\prime },\vec{a},\vec{k}}-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2}\gg \unicode[STIX]{x1D702}^{400C_{1}}1_{i^{\prime }=i}.\end{eqnarray}$$
Assuming this bound, we conclude that
 $$\begin{eqnarray}\displaystyle \mathbb{E}\operatorname{E}_{i^{\prime }}(\mathbf{N}) & {\leqslant} & \displaystyle \mathop{\sum }_{\vec{a},\vec{k}}\mathbb{P}(\vec{\mathbf{a}}=\vec{a},\vec{\mathbf{k}}=\vec{k})\mathbb{E}|1_{A_{(i^{\prime })}}(a_{(i^{\prime })}+k_{i^{\prime }}+\mathbf{h}_{i^{\prime }})-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}|1_{A_{(i^{\prime })}}(\mathbf{a}_{(i^{\prime })}+\mathbf{k}_{i^{\prime }}+\mathbf{h}_{i^{\prime }})-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2}-\unicode[STIX]{x1D702}^{500C_{1}}1_{i^{\prime }=i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}\operatorname{E}_{i^{\prime }}(\mathbf{N}) & {\leqslant} & \displaystyle \mathop{\sum }_{\vec{a},\vec{k}}\mathbb{P}(\vec{\mathbf{a}}=\vec{a},\vec{\mathbf{k}}=\vec{k})\mathbb{E}|1_{A_{(i^{\prime })}}(a_{(i^{\prime })}+k_{i^{\prime }}+\mathbf{h}_{i^{\prime }})-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2}\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}|1_{A_{(i^{\prime })}}(\mathbf{a}_{(i^{\prime })}+\mathbf{k}_{i^{\prime }}+\mathbf{h}_{i^{\prime }})-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2}-\unicode[STIX]{x1D702}^{500C_{1}}1_{i^{\prime }=i}.\nonumber\end{eqnarray}$$
By applying Lemma 4.4 twice as in the proof of (9.27) to replace
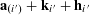 $\mathbf{a}_{(i^{\prime })}+\mathbf{k}_{i^{\prime }}+\mathbf{h}_{i^{\prime }}$
by
$\mathbf{a}_{(i^{\prime })}+\mathbf{k}_{i^{\prime }}+\mathbf{h}_{i^{\prime }}$
by
![]() $\mathbf{a}_{(i^{\prime })}$
for
$\mathbf{a}_{(i^{\prime })}$
for
 $i^{\prime }=2,3,4$
(and by using Lemma 4.4 six times for
$i^{\prime }=2,3,4$
(and by using Lemma 4.4 six times for
![]() $i^{\prime }=1$
, after writing
$i^{\prime }=1$
, after writing
![]() $\mathbf{a}_{(1)}$
in terms of
$\mathbf{a}_{(1)}$
in terms of
 $\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)}$
, and similarly for
$\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)}$
, and similarly for
![]() $\mathbf{k}_{(1)}$
and
$\mathbf{k}_{(1)}$
and
![]() $\mathbf{h}_{(1)}$
) we thus have
$\mathbf{h}_{(1)}$
) we thus have
 $$\begin{eqnarray}\mathbb{E}\operatorname{E}_{i^{\prime }}(\mathbf{N})\leqslant \mathbb{E}|1_{A_{(i^{\prime })}}(\mathbf{a}_{(i^{\prime })})-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2}-\unicode[STIX]{x1D702}^{500C_{1}}1_{i^{\prime }=i}+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}\operatorname{E}_{i^{\prime }}(\mathbf{N})\leqslant \mathbb{E}|1_{A_{(i^{\prime })}}(\mathbf{a}_{(i^{\prime })})-\unicode[STIX]{x1D6FC}_{i^{\prime }}|^{2}-\unicode[STIX]{x1D702}^{500C_{1}}1_{i^{\prime }=i}+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}}).\end{eqnarray}$$
This will give (9.28) as soon as we establish (9.31). This is trivial for
![]() $i^{\prime }\neq i$
, so suppose that
$i^{\prime }\neq i$
, so suppose that
![]() $i=i$
. By (9.30) and (9.21), it suffices to show that
$i=i$
. By (9.30) and (9.21), it suffices to show that
 $$\begin{eqnarray}\mathop{\sum }_{\vec{a},\vec{k}}\mathbb{P}(\vec{\mathbf{a}}=\vec{a},\vec{\mathbf{k}}=\vec{k})|\mathbb{E}f_{i}(a_{(i)}+k_{i}+\mathbf{h}_{i})|^{2}\gg \unicode[STIX]{x1D702}^{400C_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\vec{a},\vec{k}}\mathbb{P}(\vec{\mathbf{a}}=\vec{a},\vec{\mathbf{k}}=\vec{k})|\mathbb{E}f_{i}(a_{(i)}+k_{i}+\mathbf{h}_{i})|^{2}\gg \unicode[STIX]{x1D702}^{400C_{1}}.\end{eqnarray}$$
To prove this, we introduce random variables
![]() $\mathbf{n}_{0},\mathbf{n}_{1}$
drawn independently and regularly from
$\mathbf{n}_{0},\mathbf{n}_{1}$
drawn independently and regularly from
 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+10})$
and
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+10})$
and
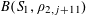 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+11})$
independently of all previous variables. From (9.29) we have
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+11})$
independently of all previous variables. From (9.29) we have
 $$\begin{eqnarray}|\mathbb{E}f_{i}(\mathbf{a}_{(i)}+\mathbf{n}_{0}+\mathbf{n}_{1})g(\mathbf{n}_{0},\mathbf{a}_{(i)})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}^{200C_{1}}\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f_{i}(\mathbf{a}_{(i)}+\mathbf{n}_{0}+\mathbf{n}_{1})g(\mathbf{n}_{0},\mathbf{a}_{(i)})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1})|\gg \unicode[STIX]{x1D702}^{200C_{1}}\end{eqnarray}$$
for some
![]() $1$
-bounded function
$1$
-bounded function
![]() $g$
. After using Lemma 4.4 to compare
$g$
. After using Lemma 4.4 to compare
![]() $\mathbf{n}_{1}$
and
$\mathbf{n}_{1}$
and
![]() $\mathbf{n}_{1}+\mathbf{h}_{i}$
for each fixed choice of
$\mathbf{n}_{1}+\mathbf{h}_{i}$
for each fixed choice of
![]() $\mathbf{n}_{0}$
and
$\mathbf{n}_{0}$
and
![]() $\mathbf{a}_{(i)}$
, we conclude that
$\mathbf{a}_{(i)}$
, we conclude that
 $$\begin{eqnarray}|\mathbb{E}f_{i}(\mathbf{a}_{(i)}+\mathbf{n}_{0}+\mathbf{n}_{1}+\mathbf{h}_{i})g(\mathbf{n}_{0},\mathbf{a}_{(i)})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})(\mathbf{n}_{1}+\mathbf{h}_{i}))|\gg \unicode[STIX]{x1D702}^{200C_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f_{i}(\mathbf{a}_{(i)}+\mathbf{n}_{0}+\mathbf{n}_{1}+\mathbf{h}_{i})g(\mathbf{n}_{0},\mathbf{a}_{(i)})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})(\mathbf{n}_{1}+\mathbf{h}_{i}))|\gg \unicode[STIX]{x1D702}^{200C_{1}}.\end{eqnarray}$$
But we have
 $$\begin{eqnarray}\biggl\|\frac{\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{h}_{i}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \Vert \mathbf{h}_{i}\Vert _{S_{1}\cup \{\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\}}\ll \unicode[STIX]{x1D70C}_{j+l_{i}+20}\end{eqnarray}$$
$$\begin{eqnarray}\biggl\|\frac{\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{h}_{i}}{p}\biggr\|_{\mathbb{R}/\mathbb{Z}}\leqslant \Vert \mathbf{h}_{i}\Vert _{S_{1}\cup \{\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\}}\ll \unicode[STIX]{x1D70C}_{j+l_{i}+20}\end{eqnarray}$$
and hence by (2.2)
 $$\begin{eqnarray}e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})(\mathbf{n}_{1}+\mathbf{h}_{i}))=e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1})+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}}).\end{eqnarray}$$
$$\begin{eqnarray}e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})(\mathbf{n}_{1}+\mathbf{h}_{i}))=e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1})+O(\unicode[STIX]{x1D702}^{10^{3}C_{1}}).\end{eqnarray}$$
We conclude that
 $$\begin{eqnarray}|\mathbb{E}(f_{i}(\mathbf{a}_{(i)}+\mathbf{n}_{0}+\mathbf{n}_{1}+\mathbf{h}_{i})g(\mathbf{n}_{0},\mathbf{a}_{(i)})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1}))|\gg \unicode[STIX]{x1D702}^{200C_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(f_{i}(\mathbf{a}_{(i)}+\mathbf{n}_{0}+\mathbf{n}_{1}+\mathbf{h}_{i})g(\mathbf{n}_{0},\mathbf{a}_{(i)})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1}))|\gg \unicode[STIX]{x1D702}^{200C_{1}}.\end{eqnarray}$$
For fixed choices of
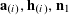 $\mathbf{a}_{(i)},\mathbf{h}_{(i)},\mathbf{n}_{1}$
, we see from Lemma 4.4 that
$\mathbf{a}_{(i)},\mathbf{h}_{(i)},\mathbf{n}_{1}$
, we see from Lemma 4.4 that
![]() $\mathbf{k}_{i}$
and
$\mathbf{k}_{i}$
and
![]() $\mathbf{n}_{0}+\mathbf{n}_{1}$
differ in total variation by
$\mathbf{n}_{0}+\mathbf{n}_{1}$
differ in total variation by
 $O(\unicode[STIX]{x1D702}^{10^{3}C_{1}})$
. Thus we have
$O(\unicode[STIX]{x1D702}^{10^{3}C_{1}})$
. Thus we have
 $$\begin{eqnarray}|\mathbb{E}(f_{i}(\mathbf{a}_{(i)}+\mathbf{k}_{i}+\mathbf{h}_{i})g(\mathbf{k}_{i}-\mathbf{n}_{1},a_{(i)})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1}))|\gg \unicode[STIX]{x1D702}^{200C_{1}},\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}(f_{i}(\mathbf{a}_{(i)}+\mathbf{k}_{i}+\mathbf{h}_{i})g(\mathbf{k}_{i}-\mathbf{n}_{1},a_{(i)})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1}))|\gg \unicode[STIX]{x1D702}^{200C_{1}},\end{eqnarray}$$
and the claim now follows after using Lemma 2.1 to eliminate the
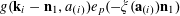 $g(\mathbf{k}_{i}-\mathbf{n}_{1},a_{(i)})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1})$
factor.◻
$g(\mathbf{k}_{i}-\mathbf{n}_{1},a_{(i)})e_{p}(-\unicode[STIX]{x1D709}(\mathbf{a}_{(i)})\mathbf{n}_{1})$
factor.◻
A useful consequence of the bounds in Theorem 9.9(ii) is the following weak mixing bound, which roughly speaking asserts that the convolution of
![]() $1_{A_{(i)}}$
with a bounded function is essentially constant.
$1_{A_{(i)}}$
with a bounded function is essentially constant.
Lemma 9.10. Let the notation and hypotheses be as above, and let
![]() $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
![]() $\unicode[STIX]{x1D709}$
be as in Theorem 9.2. Let
$\unicode[STIX]{x1D709}$
be as in Theorem 9.2. Let
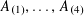 $A_{(1)},\ldots ,A_{(4)}$
be as in Theorem 9.7, and let
$A_{(1)},\ldots ,A_{(4)}$
be as in Theorem 9.7, and let
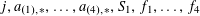 $j,a_{(1),\ast },\ldots ,a_{(4),\ast },S_{1},f_{1},\ldots ,f_{4}$
be as in Theorem 9.9. Then for any
$j,a_{(1),\ast },\ldots ,a_{(4),\ast },S_{1},f_{1},\ldots ,f_{4}$
be as in Theorem 9.9. Then for any
 $i=1,2,3,4$
, any
$i=1,2,3,4$
, any
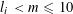 $l_{i}<m\leqslant 10$
, and any
$l_{i}<m\leqslant 10$
, and any
![]() $1$
-bounded function
$1$
-bounded function
 $g:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
, one has
$g:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
, one has
 $$\begin{eqnarray}\mathop{\sum }_{n}\mathbb{P}(\mathbf{n}=n)|\mathbb{E}f_{i}(n-\mathbf{k})g(\mathbf{k})|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n}\mathbb{P}(\mathbf{n}=n)|\mathbb{E}f_{i}(n-\mathbf{k})g(\mathbf{k})|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}},\end{eqnarray}$$
where
![]() $\mathbf{n},\mathbf{k}$
are drawn independently and regularly from
$\mathbf{n},\mathbf{k}$
are drawn independently and regularly from
 $a_{(i),\ast }+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
and
$a_{(i),\ast }+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
and
 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+m})$
respectively. Dually, for any
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+m})$
respectively. Dually, for any
![]() $1$
-bounded function
$1$
-bounded function
 $G:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
, one has
$G:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
, one has
 $$\begin{eqnarray}\mathop{\sum }_{k}\mathbb{P}(\mathbf{k}=k)|\mathbb{E}f_{i}(\mathbf{n}-k)G(\mathbf{n})|\ll \unicode[STIX]{x1D702}^{25C_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k}\mathbb{P}(\mathbf{k}=k)|\mathbb{E}f_{i}(\mathbf{n}-k)G(\mathbf{n})|\ll \unicode[STIX]{x1D702}^{25C_{1}}.\end{eqnarray}$$
Proof. In preparation for invoking Theorem 9.9(ii), we introduce random variables
 $\mathbf{h}_{0},\mathbf{h}_{1},\mathbf{h}_{1}^{\prime }$
drawn independently and regularly from
$\mathbf{h}_{0},\mathbf{h}_{1},\mathbf{h}_{1}^{\prime }$
drawn independently and regularly from
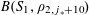 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+10})$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+10})$
,
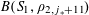 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+11})$
, and
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+11})$
, and
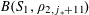 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+11})$
respectively, independently of
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+11})$
respectively, independently of
![]() $\mathbf{n}$
and
$\mathbf{n}$
and
![]() $\mathbf{k}$
. Using Lemma 4.4 to compare
$\mathbf{k}$
. Using Lemma 4.4 to compare
![]() $\mathbf{n},\mathbf{k}$
with
$\mathbf{n},\mathbf{k}$
with
![]() $\mathbf{n}+\mathbf{h}_{0}$
,
$\mathbf{n}+\mathbf{h}_{0}$
,
![]() $\mathbf{k}-\mathbf{h}_{1}$
respectively, we may transform (9.33) to the estimate
$\mathbf{k}-\mathbf{h}_{1}$
respectively, we may transform (9.33) to the estimate
 $$\begin{eqnarray}\mathop{\sum }_{n,h_{0}}\mathbb{P}(\mathbf{n}=n,\mathbf{h}_{0}=h_{0})|\mathbb{E}(f_{i}(n+h_{0}-\mathbf{k}-\mathbf{h}_{1})g(\mathbf{k}-\mathbf{h}_{1}))|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n,h_{0}}\mathbb{P}(\mathbf{n}=n,\mathbf{h}_{0}=h_{0})|\mathbb{E}(f_{i}(n+h_{0}-\mathbf{k}-\mathbf{h}_{1})g(\mathbf{k}-\mathbf{h}_{1}))|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}.\end{eqnarray}$$
By the triangle inequality in
![]() $L^{2}$
, it thus suffices to show that
$L^{2}$
, it thus suffices to show that
 $$\begin{eqnarray}\mathop{\sum }_{n,h_{0}}\mathbb{P}(\mathbf{n}=n,\mathbf{h}_{0}=h_{0})|\mathbb{E}(f_{i}(n+h_{0}-k-\mathbf{h}_{1})g(k-\mathbf{h}_{1}))|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n,h_{0}}\mathbb{P}(\mathbf{n}=n,\mathbf{h}_{0}=h_{0})|\mathbb{E}(f_{i}(n+h_{0}-k-\mathbf{h}_{1})g(k-\mathbf{h}_{1}))|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}\end{eqnarray}$$
for all
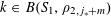 $k\in B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+m})$
.
$k\in B(S_{1},\unicode[STIX]{x1D70C}_{2,j_{\ast }+m})$
.
Fix
![]() $k$
. We may expand out the left-hand side of (9.35) as
$k$
. We may expand out the left-hand side of (9.35) as
 $$\begin{eqnarray}\mathbb{E}f_{i}(\mathbf{n}+\mathbf{h}_{0}-\mathbf{h}_{1}-k)g(k-\mathbf{h}_{1})f_{i}(\mathbf{n}+\mathbf{h}_{0}-\mathbf{h}_{1}^{\prime }-k)g(k-\mathbf{h}_{1}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f_{i}(\mathbf{n}+\mathbf{h}_{0}-\mathbf{h}_{1}-k)g(k-\mathbf{h}_{1})f_{i}(\mathbf{n}+\mathbf{h}_{0}-\mathbf{h}_{1}^{\prime }-k)g(k-\mathbf{h}_{1}^{\prime }).\end{eqnarray}$$
Using Lemma 4.4 to compare
![]() $\mathbf{n}$
with
$\mathbf{n}$
with
 $\mathbf{n}+\mathbf{h}_{0}-\mathbf{h}_{1}-\mathbf{h}_{1}^{\prime }-k$
, we can thus rewrite (9.35) as
$\mathbf{n}+\mathbf{h}_{0}-\mathbf{h}_{1}-\mathbf{h}_{1}^{\prime }-k$
, we can thus rewrite (9.35) as
 $$\begin{eqnarray}|\mathbb{E}f_{i}(\mathbf{n}+\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })g(k-\mathbf{h}_{1})f_{i}(\mathbf{n}+\mathbf{h}_{0}+\mathbf{h}_{1})g(k-\mathbf{h}_{1}^{\prime })|\ll \unicode[STIX]{x1D702}^{50C_{1}},\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}f_{i}(\mathbf{n}+\mathbf{h}_{0}+\mathbf{h}_{1}^{\prime })g(k-\mathbf{h}_{1})f_{i}(\mathbf{n}+\mathbf{h}_{0}+\mathbf{h}_{1})g(k-\mathbf{h}_{1}^{\prime })|\ll \unicode[STIX]{x1D702}^{50C_{1}},\end{eqnarray}$$
which by the triangle inequality and the
![]() $1$
-boundedness of
$1$
-boundedness of
![]() $g$
would follow from
$g$
would follow from
 $$\begin{eqnarray}\mathop{\sum }_{n,h_{1},h_{1}^{\prime }}\mathbb{P}(\mathbf{n}=n,\mathbf{h}_{1}=h_{1},\mathbf{h}_{1}^{\prime }=h_{1})|\mathbb{E}f_{i}(n+\mathbf{h}_{0}+h_{1}^{\prime })f_{i}(n+\mathbf{h}_{0}+h_{1})|\ll \unicode[STIX]{x1D702}^{50C_{1}},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n,h_{1},h_{1}^{\prime }}\mathbb{P}(\mathbf{n}=n,\mathbf{h}_{1}=h_{1},\mathbf{h}_{1}^{\prime }=h_{1})|\mathbb{E}f_{i}(n+\mathbf{h}_{0}+h_{1}^{\prime })f_{i}(n+\mathbf{h}_{0}+h_{1})|\ll \unicode[STIX]{x1D702}^{50C_{1}},\end{eqnarray}$$
which by Cauchy–Schwarz will follow in turn from
 $$\begin{eqnarray}\mathop{\sum }_{n,h_{1},h_{1}^{\prime }}\mathbb{P}(\mathbf{n}=n,\mathbf{h}_{1}=h_{1},\mathbf{h}_{1}^{\prime }=h_{1})|\mathbb{E}f_{i}(n+\mathbf{h}_{0}+h_{1}^{\prime })f_{i}(n+\mathbf{h}_{0}+h_{1})|^{2}\ll \unicode[STIX]{x1D702}^{100C_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n,h_{1},h_{1}^{\prime }}\mathbb{P}(\mathbf{n}=n,\mathbf{h}_{1}=h_{1},\mathbf{h}_{1}^{\prime }=h_{1})|\mathbb{E}f_{i}(n+\mathbf{h}_{0}+h_{1}^{\prime })f_{i}(n+\mathbf{h}_{0}+h_{1})|^{2}\ll \unicode[STIX]{x1D702}^{100C_{1}}.\end{eqnarray}$$
But this follows from Theorem 9.9(ii) (relabelling
![]() $\mathbf{n}$
as
$\mathbf{n}$
as
![]() $\mathbf{a}_{(i)}$
).
$\mathbf{a}_{(i)}$
).
Finally, we show (9.34). By subtracting
![]() $\mathbb{E}G(\mathbf{n})$
from
$\mathbb{E}G(\mathbf{n})$
from
![]() $G$
(and dividing by
$G$
(and dividing by
![]() $2$
to recover
$2$
to recover
![]() $1$
-boundedness), we may assume that
$1$
-boundedness), we may assume that
 $\mathbb{E}G(\mathbf{n})=0$
. It then suffices to show that
$\mathbb{E}G(\mathbf{n})=0$
. It then suffices to show that
 $$\begin{eqnarray}\mathop{\sum }_{k}\mathbb{P}(\mathbf{k}=k)g(k)\mathbb{E}1_{A_{(i)}}(\mathbf{n}-k)G(\mathbf{n})\ll \unicode[STIX]{x1D702}^{25C_{1}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k}\mathbb{P}(\mathbf{k}=k)g(k)\mathbb{E}1_{A_{(i)}}(\mathbf{n}-k)G(\mathbf{n})\ll \unicode[STIX]{x1D702}^{25C_{1}}\end{eqnarray}$$
for any
![]() $1$
-bounded function
$1$
-bounded function
![]() $g$
. But the left-hand side may be rearranged as
$g$
. But the left-hand side may be rearranged as
 $$\begin{eqnarray}\mathop{\sum }_{n}\mathbb{P}(\mathbf{n}=n)G(n)(\mathbb{E}1_{A_{(i)}}(n-\mathbf{k})g(\mathbf{k})-\unicode[STIX]{x1D6FC}_{i}\mathbb{E}g(\mathbf{k}))\ll \unicode[STIX]{x1D702}^{25C_{1}},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n}\mathbb{P}(\mathbf{n}=n)G(n)(\mathbb{E}1_{A_{(i)}}(n-\mathbf{k})g(\mathbf{k})-\unicode[STIX]{x1D6FC}_{i}\mathbb{E}g(\mathbf{k}))\ll \unicode[STIX]{x1D702}^{25C_{1}},\end{eqnarray}$$
and the claim follows from (9.33) and the Cauchy–Schwarz inequality. ◻
9.11 Fifth step: a frequency function
 $\unicode[STIX]{x1D709}^{\prime }$
that is approximately linear 99% of the time on a Bohr neighbourhood
$\unicode[STIX]{x1D709}^{\prime }$
that is approximately linear 99% of the time on a Bohr neighbourhood
The next step is to obtain additive structure on almost all of a Bohr neighbourhood, rather than just the subsets
![]() $A_{(i)}$
.
$A_{(i)}$
.
Theorem 9.12. Let the notation and hypotheses be as in Theorem 8.1, and let
![]() $\unicode[STIX]{x1D709}$
be as in Theorem 9.2. Let
$\unicode[STIX]{x1D709}$
be as in Theorem 9.2. Let
 $A_{(1)},\ldots ,A_{(4)}$
be as in Theorem 9.7, and let
$A_{(1)},\ldots ,A_{(4)}$
be as in Theorem 9.7, and let
 $j,a_{(1),1},a_{(2),1},a_{(3),1},a_{(4),1},S_{1},\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{4}$
be as in Theorem 9.9. Let
$j,a_{(1),1},a_{(2),1},a_{(3),1},a_{(4),1},S_{1},\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{4}$
be as in Theorem 9.9. Let
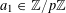 $a_{1}\in \mathbb{Z}/p\mathbb{Z}$
be the quantity
$a_{1}\in \mathbb{Z}/p\mathbb{Z}$
be the quantity
 $$\begin{eqnarray}a_{1}:=a_{(1),1}+a_{(2),1}=a_{(3),1}+a_{(4),1},\end{eqnarray}$$
$$\begin{eqnarray}a_{1}:=a_{(1),1}+a_{(2),1}=a_{(3),1}+a_{(4),1},\end{eqnarray}$$
and let
![]() $\mathbf{a}$
and
$\mathbf{a}$
and
![]() $\mathbf{a}_{(2)}$
be drawn regularly and independently from
$\mathbf{a}_{(2)}$
be drawn regularly and independently from
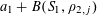 $a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
and
$a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
and
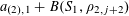 $a_{(2),1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j+2})$
respectively. Then there is a function
$a_{(2),1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j+2})$
respectively. Then there is a function
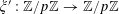 $\unicode[STIX]{x1D709}^{\prime }:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
, such that with probability at least
$\unicode[STIX]{x1D709}^{\prime }:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{Z}/p\mathbb{Z}$
, such that with probability at least
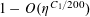 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
![]() $\mathbf{a}$
attains a value
$\mathbf{a}$
attains a value
![]() $a$
for which we have the estimates
$a$
for which we have the estimates
 $$\begin{eqnarray}\mathbb{E}1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(1)}}(a-\mathbf{a}_{(2)})=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}+O(\unicode[STIX]{x1D702}^{20C_{1}}),\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(1)}}(a-\mathbf{a}_{(2)})=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}+O(\unicode[STIX]{x1D702}^{20C_{1}}),\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(a-\mathbf{a}_{(2)}\in A_{(1)};a_{(2)}\in A_{(2)};\Vert \unicode[STIX]{x1D709}^{\prime }(a)-\unicode[STIX]{x1D709}(a-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>\frac{1}{\unicode[STIX]{x1D70C}_{3}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \ll \unicode[STIX]{x1D702}^{C_{1}/200}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(a-\mathbf{a}_{(2)}\in A_{(1)};a_{(2)}\in A_{(2)};\Vert \unicode[STIX]{x1D709}^{\prime }(a)-\unicode[STIX]{x1D709}(a-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>\frac{1}{\unicode[STIX]{x1D70C}_{3}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \ll \unicode[STIX]{x1D702}^{C_{1}/200}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}.\end{eqnarray}$$
Proof. Let
![]() $\mathbf{a}$
be drawn regularly from
$\mathbf{a}$
be drawn regularly from
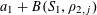 $a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
, and let
$a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
, and let
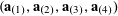 $(\mathbf{a}_{(1)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)})$
be a random additive quadruple centred at
$(\mathbf{a}_{(1)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)})$
be a random additive quadruple centred at
 $(a_{(1),1},a_{(2),1},a_{(3),1},a_{(4),1})$
with frequencies
$(a_{(1),1},a_{(2),1},a_{(3),1},a_{(4),1})$
with frequencies
![]() $S_{1}$
and scales
$S_{1}$
and scales
 $\unicode[STIX]{x1D70C}_{2,j+2},\unicode[STIX]{x1D70C}_{2,j+1},\unicode[STIX]{x1D70C}_{2,j}$
, independently of
$\unicode[STIX]{x1D70C}_{2,j+2},\unicode[STIX]{x1D70C}_{2,j+1},\unicode[STIX]{x1D70C}_{2,j}$
, independently of
![]() $\mathbf{a}$
. From the definition of an additive quadruple, we have
$\mathbf{a}$
. From the definition of an additive quadruple, we have
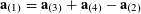 $\mathbf{a}_{(1)}=\mathbf{a}_{(3)}+\mathbf{a}_{(4)}-\mathbf{a}_{(2)}$
. From Theorem 9.9(i) we thus have
$\mathbf{a}_{(1)}=\mathbf{a}_{(3)}+\mathbf{a}_{(4)}-\mathbf{a}_{(2)}$
. From Theorem 9.9(i) we thus have
 $$\begin{eqnarray}\mathbb{E}W(\mathbf{a}_{(3)}+\mathbf{a}_{(4)}-\mathbf{a}_{(2)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}W(\mathbf{a}_{(3)}+\mathbf{a}_{(4)}-\mathbf{a}_{(2)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}_{(4)})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
From Lemma 4.4 we see that once we condition
![]() $\mathbf{a}_{(2)}$
and
$\mathbf{a}_{(2)}$
and
![]() $\mathbf{a}_{(3)}$
to be fixed,
$\mathbf{a}_{(3)}$
to be fixed,
![]() $\mathbf{a}_{(4)}$
and
$\mathbf{a}_{(4)}$
and
![]() $\mathbf{a}-\mathbf{a}_{(3)}$
differ in total variation by
$\mathbf{a}-\mathbf{a}_{(3)}$
differ in total variation by
 $O(\unicode[STIX]{x1D702}^{100C_{1}})$
. Thus we may replace
$O(\unicode[STIX]{x1D702}^{100C_{1}})$
. Thus we may replace
![]() $\mathbf{a}_{(4)}$
by
$\mathbf{a}_{(4)}$
by
![]() $\mathbf{a}-\mathbf{a}_{(3)}$
in (9.38) to conclude that
$\mathbf{a}-\mathbf{a}_{(3)}$
in (9.38) to conclude that
 $$\begin{eqnarray}\mathbb{E}W(\mathbf{a}-\mathbf{a}_{(2)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}-\mathbf{a}_{(3)})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}W(\mathbf{a}-\mathbf{a}_{(2)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}-\mathbf{a}_{(3)})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
If we then define
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}:=\mathbb{E}1_{A_{(1)}}(\mathbf{a}-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(3)}}(\mathbf{a}_{(3)})1_{A_{(4)}}(\mathbf{a}-\mathbf{a}_{(3)})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}:=\mathbb{E}1_{A_{(1)}}(\mathbf{a}-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(3)}}(\mathbf{a}_{(3)})1_{A_{(4)}}(\mathbf{a}-\mathbf{a}_{(3)})\end{eqnarray}$$
then from (9.12) we see that
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}1_{A_{(1)}}(\mathbf{a}-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(3)}}(\mathbf{a}_{(3)})1_{A_{(4)}}(\mathbf{a}-\mathbf{a}_{(3)})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,1_{\operatorname{VBQ}}(\mathbf{a}-\mathbf{a}_{(2)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}-\mathbf{a}_{(3)})\ll \unicode[STIX]{x1D702}^{-C_{1}/100}\unicode[STIX]{x1D70E}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}1_{A_{(1)}}(\mathbf{a}-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(3)}}(\mathbf{a}_{(3)})1_{A_{(4)}}(\mathbf{a}-\mathbf{a}_{(3)})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,1_{\operatorname{VBQ}}(\mathbf{a}-\mathbf{a}_{(2)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},\mathbf{a}-\mathbf{a}_{(3)})\ll \unicode[STIX]{x1D702}^{-C_{1}/100}\unicode[STIX]{x1D70E}.\end{eqnarray}$$
We can express
![]() $\unicode[STIX]{x1D70E}$
in the form
$\unicode[STIX]{x1D70E}$
in the form
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}=\mathbb{E}g_{12}(\mathbf{a})g_{34}(\mathbf{a}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}=\mathbb{E}g_{12}(\mathbf{a})g_{34}(\mathbf{a}),\end{eqnarray}$$
where
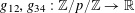 $g_{12},g_{34}:\mathbb{Z}/p/\mathbb{Z}\rightarrow \mathbb{R}$
are the functions
$g_{12},g_{34}:\mathbb{Z}/p/\mathbb{Z}\rightarrow \mathbb{R}$
are the functions
 $$\begin{eqnarray}g_{12}(a):=\mathbb{E}1_{A_{(1)}}(a-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})\end{eqnarray}$$
$$\begin{eqnarray}g_{12}(a):=\mathbb{E}1_{A_{(1)}}(a-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})\end{eqnarray}$$
and
 $$\begin{eqnarray}g_{34}(a):=\mathbb{E}1_{A_{(3)}}(\mathbf{a}_{(3)})1_{A_{(4)}}(a-\mathbf{a}_{(3)}).\end{eqnarray}$$
$$\begin{eqnarray}g_{34}(a):=\mathbb{E}1_{A_{(3)}}(\mathbf{a}_{(3)})1_{A_{(4)}}(a-\mathbf{a}_{(3)}).\end{eqnarray}$$
From Lemma 9.10, we have
 $$\begin{eqnarray}\mathop{\sum }_{n}\mathbb{P}(\mathbf{n}=n)|\mathbb{E}f_{1}(n-\mathbf{k})1_{A_{(2)}}(a_{(2),1}+\mathbf{k})|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n}\mathbb{P}(\mathbf{n}=n)|\mathbb{E}f_{1}(n-\mathbf{k})1_{A_{(2)}}(a_{(2),1}+\mathbf{k})|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}\end{eqnarray}$$
if
![]() $\mathbf{n},\mathbf{k}$
are drawn independently and regularly from
$\mathbf{n},\mathbf{k}$
are drawn independently and regularly from
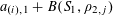 $a_{(i),1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
and
$a_{(i),1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
and
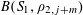 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+m})$
respectively. Note that the pair
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+m})$
respectively. Note that the pair
![]() $(\mathbf{n},\mathbf{k})$
has the same distribution as
$(\mathbf{n},\mathbf{k})$
has the same distribution as
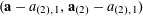 $(\mathbf{a}-a_{(2),1},\mathbf{a}_{(2)}-a_{(2),1})$
, thus
$(\mathbf{a}-a_{(2),1},\mathbf{a}_{(2)}-a_{(2),1})$
, thus
 $$\begin{eqnarray}\mathop{\sum }_{a}\mathbb{P}(\mathbf{a}=a)|\mathbb{E}f_{1}(a-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{a}\mathbb{P}(\mathbf{a}=a)|\mathbb{E}f_{1}(a-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}.\end{eqnarray}$$
From (9.21), (9.22), (9.42) we have
 $$\begin{eqnarray}\mathbb{E}f_{1}(a-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})=g_{12}(a)-\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}f_{1}(a-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})=g_{12}(a)-\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\end{eqnarray}$$
and thus
 $$\begin{eqnarray}\mathop{\sum }_{a}\mathbb{P}(\mathbf{a}=a)|g_{12}(a)-\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{a}\mathbb{P}(\mathbf{a}=a)|g_{12}(a)-\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}.\end{eqnarray}$$
Similarly we have
 $$\begin{eqnarray}\mathop{\sum }_{a}\mathbb{P}(\mathbf{a}=a)|g_{34}(a)-\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{a}\mathbb{P}(\mathbf{a}=a)|g_{34}(a)-\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}|^{2}\ll \unicode[STIX]{x1D702}^{50C_{1}}.\end{eqnarray}$$
From Cauchy–Schwarz and the triangle inequality we conclude that
 $$\begin{eqnarray}\mathop{\sum }_{a}\mathbb{P}(\mathbf{a}=a)|g_{12}(a)g_{34}(a)-\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}|\ll \unicode[STIX]{x1D702}^{25C_{1}},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{a}\mathbb{P}(\mathbf{a}=a)|g_{12}(a)g_{34}(a)-\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}|\ll \unicode[STIX]{x1D702}^{25C_{1}},\end{eqnarray}$$
and hence by (9.41) and the triangle inequality
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}+O(\unicode[STIX]{x1D702}^{25C_{1}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}+O(\unicode[STIX]{x1D702}^{25C_{1}}).\end{eqnarray}$$
In particular, from (9.39) one has
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
From (9.45), (9.46) and (9.40) we have
 $$\begin{eqnarray}\mathbb{E}h(\mathbf{a})\ll \unicode[STIX]{x1D702}^{C_{1}/100}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}h(\mathbf{a})\ll \unicode[STIX]{x1D702}^{C_{1}/100}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4},\end{eqnarray}$$
where
 $$\begin{eqnarray}h(a):=\mathbb{E}W(a-\mathbf{a}_{(2)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},a-\mathbf{a}_{(3)}).\end{eqnarray}$$
$$\begin{eqnarray}h(a):=\mathbb{E}W(a-\mathbf{a}_{(2)},\mathbf{a}_{(2)},\mathbf{a}_{(3)},a-\mathbf{a}_{(3)}).\end{eqnarray}$$
By Markov’s inequality, we conclude that we have
 $$\begin{eqnarray}h(\mathbf{a})\ll \unicode[STIX]{x1D702}^{C_{1}/200}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}\end{eqnarray}$$
$$\begin{eqnarray}h(\mathbf{a})\ll \unicode[STIX]{x1D702}^{C_{1}/200}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}\end{eqnarray}$$
with probability
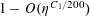 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
. Similarly, from (9.43), (9.44) and Chebyshev’s inequality we also have
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
. Similarly, from (9.43), (9.44) and Chebyshev’s inequality we also have
 $$\begin{eqnarray}g_{12}(\mathbf{a})=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}+O(\unicode[STIX]{x1D702}^{20C_{1}})\end{eqnarray}$$
$$\begin{eqnarray}g_{12}(\mathbf{a})=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}+O(\unicode[STIX]{x1D702}^{20C_{1}})\end{eqnarray}$$
and
 $$\begin{eqnarray}g_{34}(\mathbf{a})=\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}+O(\unicode[STIX]{x1D702}^{20C_{1}})\end{eqnarray}$$
$$\begin{eqnarray}g_{34}(\mathbf{a})=\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4}+O(\unicode[STIX]{x1D702}^{20C_{1}})\end{eqnarray}$$
with probability
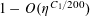 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
.
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
.
Now let
![]() $a$
be a value of
$a$
be a value of
![]() $\mathbf{a}$
be such that (9.48)–(9.50) hold. From (9.50) we have in particular that
$\mathbf{a}$
be such that (9.48)–(9.50) hold. From (9.50) we have in particular that
 $$\begin{eqnarray}\mathbb{E}1_{A_{(3)}}(\mathbf{a}_{(3)})1_{A_{(4)}}(a-\mathbf{a}_{(3)})\gg \unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4};\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}1_{A_{(3)}}(\mathbf{a}_{(3)})1_{A_{(4)}}(a-\mathbf{a}_{(3)})\gg \unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FC}_{4};\end{eqnarray}$$
comparing this with (9.48) and (9.47), we see that we may find
 $a_{(3)}(a)\in A_{(3)}$
(depending only on
$a_{(3)}(a)\in A_{(3)}$
(depending only on
![]() $a$
) with
$a$
) with
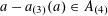 $a-a_{(3)}(a)\in A_{(4)}$
such that
$a-a_{(3)}(a)\in A_{(4)}$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}1_{A_{(1)}}(a-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})1_{\operatorname{VBQ}}(a-\mathbf{a}_{(2)},\mathbf{a}_{(2)},a_{(3)}(a),a-a_{(3)}(a))\nonumber\\ \displaystyle & & \displaystyle \quad \ll \unicode[STIX]{x1D702}^{C_{1}/200}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{E}1_{A_{(1)}}(a-\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})1_{\operatorname{VBQ}}(a-\mathbf{a}_{(2)},\mathbf{a}_{(2)},a_{(3)}(a),a-a_{(3)}(a))\nonumber\\ \displaystyle & & \displaystyle \quad \ll \unicode[STIX]{x1D702}^{C_{1}/200}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}.\nonumber\end{eqnarray}$$
If we then set
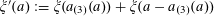 $\unicode[STIX]{x1D709}^{\prime }(a):=\unicode[STIX]{x1D709}(a_{(3)}(a))+\unicode[STIX]{x1D709}(a-a_{(3)}(a))$
(and define
$\unicode[STIX]{x1D709}^{\prime }(a):=\unicode[STIX]{x1D709}(a_{(3)}(a))+\unicode[STIX]{x1D709}(a-a_{(3)}(a))$
(and define
![]() $\unicode[STIX]{x1D709}^{\prime }(\mathbf{a})$
arbitrarily when (9.48), (9.49), or (9.50) fail), then the claims (9.36), (9.37) follow from (9.49) and the definition (9.10) of
$\unicode[STIX]{x1D709}^{\prime }(\mathbf{a})$
arbitrarily when (9.48), (9.49), or (9.50) fail), then the claims (9.36), (9.37) follow from (9.49) and the definition (9.10) of
![]() $\operatorname{VBQ}$
.◻
$\operatorname{VBQ}$
.◻
The function
![]() $\unicode[STIX]{x1D709}^{\prime }$
has better additive structure than
$\unicode[STIX]{x1D709}^{\prime }$
has better additive structure than
![]() $\unicode[STIX]{x1D709}$
, in that it respects almost all additive quadruples in a Bohr set, rather than almost all additive quadruples in a rough set. More precisely, we have the following.
$\unicode[STIX]{x1D709}$
, in that it respects almost all additive quadruples in a Bohr set, rather than almost all additive quadruples in a rough set. More precisely, we have the following.
Proposition 9.13. Let the notation and hypotheses be as in Theorem 9.12. Suppose that
![]() $\mathbf{a},\mathbf{a}^{\prime },\mathbf{h}$
are selected independently and regularly from
$\mathbf{a},\mathbf{a}^{\prime },\mathbf{h}$
are selected independently and regularly from
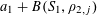 $a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
,
$a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
,
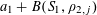 $a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
, and
$a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
, and
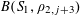 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+3})$
respectively. Then with probability
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+3})$
respectively. Then with probability
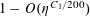 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
we have
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
we have
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}+\mathbf{h})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}^{\prime })+\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}^{\prime }+\mathbf{h})\Vert _{S}\leqslant \frac{4}{\unicode[STIX]{x1D70C}_{3}}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}+\mathbf{h})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}^{\prime })+\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}^{\prime }+\mathbf{h})\Vert _{S}\leqslant \frac{4}{\unicode[STIX]{x1D70C}_{3}}.\end{eqnarray}$$
Proof. Let
![]() $\mathbf{a}_{(2)}$
be drawn regularly from
$\mathbf{a}_{(2)}$
be drawn regularly from
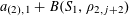 $a_{(2),1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j+2})$
, independently of
$a_{(2),1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j+2})$
, independently of
![]() $\mathbf{a},\mathbf{a}^{\prime },\mathbf{h}$
. For each
$\mathbf{a},\mathbf{a}^{\prime },\mathbf{h}$
. For each
 $a,a^{\prime },h\in \mathbb{Z}/p\mathbb{Z}$
, let
$a,a^{\prime },h\in \mathbb{Z}/p\mathbb{Z}$
, let
![]() $\mathbf{I}_{a,a^{\prime },h}$
denote the random indicator variable
$\mathbf{I}_{a,a^{\prime },h}$
denote the random indicator variable
 $$\begin{eqnarray}\mathbf{I}_{a,a^{\prime },h}:=1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)}+h)1_{A_{(1)}}(a-\mathbf{a}_{(2)})1_{A_{(1)}}(a^{\prime }-\mathbf{a}_{(2)}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{I}_{a,a^{\prime },h}:=1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)}+h)1_{A_{(1)}}(a-\mathbf{a}_{(2)})1_{A_{(1)}}(a^{\prime }-\mathbf{a}_{(2)}).\end{eqnarray}$$
Suppose that we can show that with probability
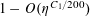 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the triple
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the triple
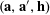 $(\mathbf{a},\mathbf{a}^{\prime },\mathbf{h})$
attains a value
$(\mathbf{a},\mathbf{a}^{\prime },\mathbf{h})$
attains a value
 $(a,a^{\prime },h)$
for which one has the estimates
$(a,a^{\prime },h)$
for which one has the estimates
 $$\begin{eqnarray}\displaystyle \mathbb{E}\mathbf{I}_{a,a^{\prime },h} & {\geqslant} & \displaystyle 0.9\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}\mathbf{I}_{a,a^{\prime },h} & {\geqslant} & \displaystyle 0.9\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathbb{E}\mathbf{I}_{a,a^{\prime },h}1_{\Vert \unicode[STIX]{x1D709}^{\prime }(a)-\unicode[STIX]{x1D709}(a-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}} & {\leqslant} & \displaystyle 0.1\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}\mathbf{I}_{a,a^{\prime },h}1_{\Vert \unicode[STIX]{x1D709}^{\prime }(a)-\unicode[STIX]{x1D709}(a-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}} & {\leqslant} & \displaystyle 0.1\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathbb{E}\mathbf{I}_{a,a^{\prime },h}1_{\Vert \unicode[STIX]{x1D709}^{\prime }(a^{\prime })-\unicode[STIX]{x1D709}(a^{\prime }-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}} & {\leqslant} & \displaystyle 0.1\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}\mathbf{I}_{a,a^{\prime },h}1_{\Vert \unicode[STIX]{x1D709}^{\prime }(a^{\prime })-\unicode[STIX]{x1D709}(a^{\prime }-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}} & {\leqslant} & \displaystyle 0.1\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathbb{E}\mathbf{I}_{a,a^{\prime },h}1_{\Vert \unicode[STIX]{x1D709}^{\prime }(a+h)-\unicode[STIX]{x1D709}(a-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)}+h)\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}} & {\leqslant} & \displaystyle 0.1\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}\mathbf{I}_{a,a^{\prime },h}1_{\Vert \unicode[STIX]{x1D709}^{\prime }(a+h)-\unicode[STIX]{x1D709}(a-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)}+h)\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}} & {\leqslant} & \displaystyle 0.1\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathbb{E}\mathbf{I}_{a,a^{\prime },h}1_{\Vert \unicode[STIX]{x1D709}^{\prime }(a^{\prime }+h)-\unicode[STIX]{x1D709}(a^{\prime }-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)}+h)\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}} & {\leqslant} & \displaystyle 0.1\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{E}\mathbf{I}_{a,a^{\prime },h}1_{\Vert \unicode[STIX]{x1D709}^{\prime }(a^{\prime }+h)-\unicode[STIX]{x1D709}(a^{\prime }-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)}+h)\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}} & {\leqslant} & \displaystyle 0.1\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
Assuming these estimates, we conclude from the union bound that with probability
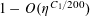 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
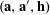 $(\mathbf{a},\mathbf{a}^{\prime },\mathbf{h})$
attains a value
$(\mathbf{a},\mathbf{a}^{\prime },\mathbf{h})$
attains a value
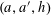 $(a,a^{\prime },h)$
for which there exists at least one element
$(a,a^{\prime },h)$
for which there exists at least one element
![]() $a_{(2)}$
of
$a_{(2)}$
of
![]() $\mathbb{Z}/p\mathbb{Z}$
obeying the constraints
$\mathbb{Z}/p\mathbb{Z}$
obeying the constraints
 $$\begin{eqnarray}\displaystyle a_{(2)},a_{(2)}+h & \in & \displaystyle A_{(2)},\nonumber\\ \displaystyle a-a_{(2)},a^{\prime }-a_{(2)} & \in & \displaystyle A_{(1)},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(a)-\unicode[STIX]{x1D709}(a-a_{(2)})-\unicode[STIX]{x1D709}(a_{(2)})\Vert _{S} & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(a^{\prime })-\unicode[STIX]{x1D709}(a^{\prime }-a_{(2)})-\unicode[STIX]{x1D709}(a_{(2)})\Vert _{S} & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(a+h)-\unicode[STIX]{x1D709}(a-a_{(2)})-\unicode[STIX]{x1D709}(a_{(2)}+h)\Vert _{S} & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(a^{\prime }+h)-\unicode[STIX]{x1D709}(a^{\prime }-a_{(2)})-\unicode[STIX]{x1D709}(a_{(2)}+h)\Vert _{S} & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{(2)},a_{(2)}+h & \in & \displaystyle A_{(2)},\nonumber\\ \displaystyle a-a_{(2)},a^{\prime }-a_{(2)} & \in & \displaystyle A_{(1)},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(a)-\unicode[STIX]{x1D709}(a-a_{(2)})-\unicode[STIX]{x1D709}(a_{(2)})\Vert _{S} & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(a^{\prime })-\unicode[STIX]{x1D709}(a^{\prime }-a_{(2)})-\unicode[STIX]{x1D709}(a_{(2)})\Vert _{S} & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(a+h)-\unicode[STIX]{x1D709}(a-a_{(2)})-\unicode[STIX]{x1D709}(a_{(2)}+h)\Vert _{S} & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(a^{\prime }+h)-\unicode[STIX]{x1D709}(a^{\prime }-a_{(2)})-\unicode[STIX]{x1D709}(a_{(2)}+h)\Vert _{S} & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}}\nonumber\end{eqnarray}$$
and (9.51) then follows from the triangle inequality.
It remains to establish (9.52)–(9.56). We first prove (9.53). By Markov’s inequality, it suffices to show that
 $$\begin{eqnarray}\mathbb{E}\mathbf{I}_{\mathbf{a},\mathbf{a}^{\prime },\mathbf{h}}1_{\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}(\mathbf{a}-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}}\ll \unicode[STIX]{x1D702}^{C_{1}/200}\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}\mathbf{I}_{\mathbf{a},\mathbf{a}^{\prime },\mathbf{h}}1_{\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}(\mathbf{a}-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}}\ll \unicode[STIX]{x1D702}^{C_{1}/200}\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
We rewrite the left-hand side as
 $$\begin{eqnarray}\mathbb{E}g_{1}(\mathbf{a}_{(2)})g_{2}(\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(1)}}(\mathbf{a}-\mathbf{a}_{(2)})1_{\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}(\mathbf{a}-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}g_{1}(\mathbf{a}_{(2)})g_{2}(\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(1)}}(\mathbf{a}-\mathbf{a}_{(2)})1_{\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}(\mathbf{a}-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
where
 $$\begin{eqnarray}g_{1}(a_{(2)}):=\mathbb{E}1_{A_{(1)}}(\mathbf{a}^{\prime }-a_{(2)})\end{eqnarray}$$
$$\begin{eqnarray}g_{1}(a_{(2)}):=\mathbb{E}1_{A_{(1)}}(\mathbf{a}^{\prime }-a_{(2)})\end{eqnarray}$$
and
 $$\begin{eqnarray}g_{2}(a_{(2)}):=\mathbb{E}1_{A_{(2)}}(a_{(2)}+\mathbf{h}).\end{eqnarray}$$
$$\begin{eqnarray}g_{2}(a_{(2)}):=\mathbb{E}1_{A_{(2)}}(a_{(2)}+\mathbf{h}).\end{eqnarray}$$
But from (9.37) we have
 $$\begin{eqnarray}\mathbb{E}1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(1)}}(\mathbf{a}-\mathbf{a}_{(2)})1_{\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}(\mathbf{a}-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}}\ll \unicode[STIX]{x1D702}^{C_{1}/200}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(1)}}(\mathbf{a}-\mathbf{a}_{(2)})1_{\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}(\mathbf{a}-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}>1/\unicode[STIX]{x1D70C}_{3}}\ll \unicode[STIX]{x1D702}^{C_{1}/200}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2},\end{eqnarray}$$
from Lemma 4.4 one has
 $$\begin{eqnarray}g_{1}(\mathbf{a}_{(2)})=\unicode[STIX]{x1D6FC}_{1}+O(\unicode[STIX]{x1D702}^{10C_{1}})\end{eqnarray}$$
$$\begin{eqnarray}g_{1}(\mathbf{a}_{(2)})=\unicode[STIX]{x1D6FC}_{1}+O(\unicode[STIX]{x1D702}^{10C_{1}})\end{eqnarray}$$
and from (9.33) one has
 $$\begin{eqnarray}g_{2}(\mathbf{a}_{(2)})=\unicode[STIX]{x1D6FC}_{2}+O(\unicode[STIX]{x1D702}^{10C_{1}})\end{eqnarray}$$
$$\begin{eqnarray}g_{2}(\mathbf{a}_{(2)})=\unicode[STIX]{x1D6FC}_{2}+O(\unicode[STIX]{x1D702}^{10C_{1}})\end{eqnarray}$$
with probability
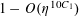 $1-O(\unicode[STIX]{x1D702}^{10C_{1}})$
(for example), with the trivial bound
$1-O(\unicode[STIX]{x1D702}^{10C_{1}})$
(for example), with the trivial bound
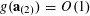 $g(\mathbf{a}_{(2)})=O(1)$
otherwise, and the claim (9.53) then follows from (9.46).
$g(\mathbf{a}_{(2)})=O(1)$
otherwise, and the claim (9.53) then follows from (9.46).
The proofs of (9.54)–(9.56) are similar to (9.53) and are omitted. It thus remains to prove (9.52). From (9.34) and Markov’s inequality, we see that with probability
 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
![]() $\mathbf{h}$
attains a value
$\mathbf{h}$
attains a value
![]() $h$
for which
$h$
for which
 $$\begin{eqnarray}\mathbb{E}1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)}+h)\geqslant 0.99\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}1_{A_{(2)}}(\mathbf{a}_{(2)})1_{A_{(2)}}(\mathbf{a}_{(2)}+h)\geqslant 0.99\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
For any
![]() $h$
obeying this inequality, define
$h$
obeying this inequality, define
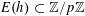 $E(h)\subset \mathbb{Z}/p\mathbb{Z}$
to be the set
$E(h)\subset \mathbb{Z}/p\mathbb{Z}$
to be the set
 $$\begin{eqnarray}E(h):=A_{(2)}\cap (A_{(2)}-h),\end{eqnarray}$$
$$\begin{eqnarray}E(h):=A_{(2)}\cap (A_{(2)}-h),\end{eqnarray}$$
so that
 $$\begin{eqnarray}\mathbb{P}(\mathbf{a}_{(2)}\in E(h))\geqslant 0.99\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{a}_{(2)}\in E(h))\geqslant 0.99\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
By (9.33) and the Chebyshev inequality, we conclude that with probability
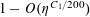 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
![]() $(\mathbf{a},\mathbf{h})$
attains a value
$(\mathbf{a},\mathbf{h})$
attains a value
![]() $(a,h)$
for which one has
$(a,h)$
for which one has
 $$\begin{eqnarray}\mathbb{P}(\mathbf{a}_{(2)}\in E(h);a-\mathbf{a}_{(2)}\in A_{(1)})\geqslant 0.98\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{a}_{(2)}\in E(h);a-\mathbf{a}_{(2)}\in A_{(1)})\geqslant 0.98\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
For any
![]() $(a,h)$
of the above form, define
$(a,h)$
of the above form, define
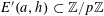 $E^{\prime }(a,h)\subset \mathbb{Z}/p\mathbb{Z}$
to be the set
$E^{\prime }(a,h)\subset \mathbb{Z}/p\mathbb{Z}$
to be the set
 $$\begin{eqnarray}E^{\prime }(a,h):=\mathbb{E}(h)\cap (a-A_{(1)}),\end{eqnarray}$$
$$\begin{eqnarray}E^{\prime }(a,h):=\mathbb{E}(h)\cap (a-A_{(1)}),\end{eqnarray}$$
then
 $$\begin{eqnarray}\mathbb{P}(\mathbf{a}_{(2)}\in E^{\prime }(a,h))\geqslant 0.98\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{a}_{(2)}\in E^{\prime }(a,h))\geqslant 0.98\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}^{2}.\end{eqnarray}$$
By one last application of (9.33) and the Chebyshev inequality, we see that with probability
 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
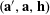 $(\mathbf{a}^{\prime },\mathbf{a},\mathbf{h})$
attains a value
$(\mathbf{a}^{\prime },\mathbf{a},\mathbf{h})$
attains a value
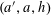 $(a^{\prime },a,h)$
for which one has
$(a^{\prime },a,h)$
for which one has
 $$\begin{eqnarray}\mathbb{P}(\mathbf{a}_{(2)}\in E^{\prime }(a,h);a^{\prime }-\mathbf{a}_{(2)}\in A_{(1)})\geqslant 0.97\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(\mathbf{a}_{(2)}\in E^{\prime }(a,h);a^{\prime }-\mathbf{a}_{(2)}\in A_{(1)})\geqslant 0.97\unicode[STIX]{x1D6FC}_{1}^{2}\unicode[STIX]{x1D6FC}_{2}^{2}\end{eqnarray}$$
which gives (9.52) as required. ◻
9.14 Sixth step: a frequency function
 $\unicode[STIX]{x1D709}^{\prime \prime }$
that is approximately linear 100% of the time on a Bohr set
$\unicode[STIX]{x1D709}^{\prime \prime }$
that is approximately linear 100% of the time on a Bohr set
We now use a standard “majority vote” argument to upgrade the “99% linear” structure of
![]() $\unicode[STIX]{x1D709}^{\prime }$
to a “100% linear” structure of a closely related function
$\unicode[STIX]{x1D709}^{\prime }$
to a “100% linear” structure of a closely related function
![]() $\unicode[STIX]{x1D709}^{\prime \prime }$
(cf. [Reference Blum, Luby and Rubinfeld5]). More precisely, one has the following.
$\unicode[STIX]{x1D709}^{\prime \prime }$
(cf. [Reference Blum, Luby and Rubinfeld5]). More precisely, one has the following.
Theorem 9.15. Let the notation and hypotheses be as in Theorem 8.1. Let
![]() $j,S_{1}$
be as in Theorem 9.9, and let
$j,S_{1}$
be as in Theorem 9.9, and let
![]() $a_{1}$
,
$a_{1}$
,
![]() $\unicode[STIX]{x1D709}^{\prime }$
be as in Theorem 9.12. Then there is a function
$\unicode[STIX]{x1D709}^{\prime }$
be as in Theorem 9.12. Then there is a function
 $\unicode[STIX]{x1D709}^{\prime \prime }:B(S_{1},\unicode[STIX]{x1D70C}_{3})\rightarrow \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}^{\prime \prime }:B(S_{1},\unicode[STIX]{x1D70C}_{3})\rightarrow \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime \prime }(n+m)-\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}^{\prime \prime }(m)\Vert _{S}\leqslant \frac{24}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime \prime }(n+m)-\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}^{\prime \prime }(m)\Vert _{S}\leqslant \frac{24}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
for all
 $n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/2)$
, and such that for any
$n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/2)$
, and such that for any
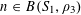 $n\in B(S_{1},\unicode[STIX]{x1D70C}_{3})$
, if
$n\in B(S_{1},\unicode[STIX]{x1D70C}_{3})$
, if
![]() $\mathbf{a}$
is drawn regularly from
$\mathbf{a}$
is drawn regularly from
 $a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
, one has
$a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
, one has
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)-\unicode[STIX]{x1D709}^{\prime \prime }(n)\Vert _{S}\leqslant \frac{8}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)-\unicode[STIX]{x1D709}^{\prime \prime }(n)\Vert _{S}\leqslant \frac{8}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
with probability
 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
.
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
.
Proof. Let
![]() $\mathbf{a},\mathbf{h}$
be drawn independently and regularly from
$\mathbf{a},\mathbf{h}$
be drawn independently and regularly from
 $a_{\ast }+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
and
$a_{\ast }+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
and
 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+3})$
respectively. From Proposition 9.13 and the pigeonhole principle, we may find
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+3})$
respectively. From Proposition 9.13 and the pigeonhole principle, we may find
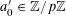 $a_{0}^{\prime }\in \mathbb{Z}/p\mathbb{Z}$
such that
$a_{0}^{\prime }\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\mathbb{P}\biggl(\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}+\mathbf{h})-\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime })+\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+\mathbf{h})\Vert _{S}\leqslant \frac{4}{\unicode[STIX]{x1D70C}_{3}}\biggr)\geqslant 1-O(\unicode[STIX]{x1D702}^{C_{1}/200}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}\biggl(\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}+\mathbf{h})-\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime })+\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+\mathbf{h})\Vert _{S}\leqslant \frac{4}{\unicode[STIX]{x1D70C}_{3}}\biggr)\geqslant 1-O(\unicode[STIX]{x1D702}^{C_{1}/200}).\end{eqnarray}$$
Fix this
![]() $a_{0}^{\prime }$
. Now let
$a_{0}^{\prime }$
. Now let
![]() $n$
by an arbitrary element of
$n$
by an arbitrary element of
 $B(S_{1},\unicode[STIX]{x1D70C}_{3})$
. Then using Lemma 4.4 to compare
$B(S_{1},\unicode[STIX]{x1D70C}_{3})$
. Then using Lemma 4.4 to compare
![]() $\mathbf{a}$
with
$\mathbf{a}$
with
![]() $\mathbf{a}-n$
and
$\mathbf{a}-n$
and
![]() $\mathbf{h}$
with
$\mathbf{h}$
with
![]() $\mathbf{h}+n$
, we obtain
$\mathbf{h}+n$
, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}+\mathbf{h})-\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime })+\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+\mathbf{h}+n)\Vert _{S}\leqslant \frac{4}{\unicode[STIX]{x1D70C}_{3}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant 1-O(\unicode[STIX]{x1D702}^{C_{1}/200}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}+\mathbf{h})-\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime })+\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+\mathbf{h}+n)\Vert _{S}\leqslant \frac{4}{\unicode[STIX]{x1D70C}_{3}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant 1-O(\unicode[STIX]{x1D702}^{C_{1}/200}).\nonumber\end{eqnarray}$$
Combining this with (9.59) and the triangle inequality, we see that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)+\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+\mathbf{h})-\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+\mathbf{h}+n)\Vert _{S}\leqslant \frac{8}{\unicode[STIX]{x1D70C}_{3}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant 1-O(\unicode[STIX]{x1D702}^{C_{1}/200}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)+\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+\mathbf{h})-\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+\mathbf{h}+n)\Vert _{S}\leqslant \frac{8}{\unicode[STIX]{x1D70C}_{3}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant 1-O(\unicode[STIX]{x1D702}^{C_{1}/200}).\nonumber\end{eqnarray}$$
Thus, by the pigeonhole principle, we may find
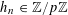 $h_{n}\in \mathbb{Z}/p\mathbb{Z}$
such that
$h_{n}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)+\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+h_{n})-\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+h_{n}+n)\Vert _{S}\leqslant \frac{8}{\unicode[STIX]{x1D70C}_{3}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant 1-O(\unicode[STIX]{x1D702}^{C_{1}/200}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)+\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+h_{n})-\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+h_{n}+n)\Vert _{S}\leqslant \frac{8}{\unicode[STIX]{x1D70C}_{3}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant 1-O(\unicode[STIX]{x1D702}^{C_{1}/200}).\nonumber\end{eqnarray}$$
If we thus define
 $$\begin{eqnarray}\unicode[STIX]{x1D709}^{\prime \prime }(n):=\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+h_{n}+n)-\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+n)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}^{\prime \prime }(n):=\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+h_{n}+n)-\unicode[STIX]{x1D709}^{\prime }(a_{0}^{\prime }+n)\end{eqnarray}$$
then we have obtained (9.58).
Now suppose that
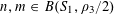 $n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/2)$
. From (9.58), we see that with probability at least
$n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/2)$
. From (9.58), we see that with probability at least
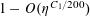 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
we have
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
we have
 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)-\unicode[STIX]{x1D709}^{\prime \prime }(n)\Vert _{S} & {\leqslant} & \displaystyle \frac{8}{\unicode[STIX]{x1D70C}_{3}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-m)-\unicode[STIX]{x1D709}^{\prime \prime }(m)\Vert _{S} & {\leqslant} & \displaystyle \frac{8}{\unicode[STIX]{x1D70C}_{3}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)-\unicode[STIX]{x1D709}^{\prime \prime }(n)\Vert _{S} & {\leqslant} & \displaystyle \frac{8}{\unicode[STIX]{x1D70C}_{3}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-m)-\unicode[STIX]{x1D709}^{\prime \prime }(m)\Vert _{S} & {\leqslant} & \displaystyle \frac{8}{\unicode[STIX]{x1D70C}_{3}},\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n-m)-\unicode[STIX]{x1D709}^{\prime \prime }(n+m)\Vert _{S}\leqslant \frac{8}{\unicode[STIX]{x1D70C}_{3}}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n-m)-\unicode[STIX]{x1D709}^{\prime \prime }(n+m)\Vert _{S}\leqslant \frac{8}{\unicode[STIX]{x1D70C}_{3}}.\end{eqnarray}$$
Using Lemma 4.4 to compare
![]() $\mathbf{a}$
with
$\mathbf{a}$
with
![]() $\mathbf{a}-n$
in the second inequality, we also conclude
$\mathbf{a}-n$
in the second inequality, we also conclude
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n-m)-\unicode[STIX]{x1D709}^{\prime \prime }(m)\Vert _{S}\leqslant \frac{8}{\unicode[STIX]{x1D70C}_{3}},\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n)-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-n-m)-\unicode[STIX]{x1D709}^{\prime \prime }(m)\Vert _{S}\leqslant \frac{8}{\unicode[STIX]{x1D70C}_{3}},\end{eqnarray}$$
with probability
 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
. Thus there is a positive probability that the first, third, and fourth estimates hold simultaneously, and the claim (9.57) follows from the triangle inequality.◻
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
. Thus there is a positive probability that the first, third, and fourth estimates hold simultaneously, and the claim (9.57) follows from the triangle inequality.◻
The function
![]() $\unicode[STIX]{x1D709}^{\prime \prime }$
is still closely related to
$\unicode[STIX]{x1D709}^{\prime \prime }$
is still closely related to
![]() $\unicode[STIX]{x1D709}$
, and in particular a variant of the correlation estimate (9.3) is obeyed by
$\unicode[STIX]{x1D709}$
, and in particular a variant of the correlation estimate (9.3) is obeyed by
![]() $\unicode[STIX]{x1D709}^{\prime \prime }$
.
$\unicode[STIX]{x1D709}^{\prime \prime }$
.
Proposition 9.16. Let the notation and hypotheses be as in the preceding theorem. Then there exist
 $a_{0}\in B(S,3\unicode[STIX]{x1D70C}_{2})$
and
$a_{0}\in B(S,3\unicode[STIX]{x1D70C}_{2})$
and
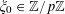 $\unicode[STIX]{x1D709}_{0}\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}_{0}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n)|\mathbb{E}f(n_{0}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+\mathbf{h})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}_{0})\mathbf{h})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n)|\mathbb{E}f(n_{0}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+\mathbf{h})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}_{0})\mathbf{h})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
where
![]() $\mathbf{n},\mathbf{n}_{0},\mathbf{h}$
are drawn independently and regularly from the Bohr sets
$\mathbf{n},\mathbf{n}_{0},\mathbf{h}$
are drawn independently and regularly from the Bohr sets
 $B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
,
 $B(S,\unicode[STIX]{x1D70C}_{0})$
,
$B(S,\unicode[STIX]{x1D70C}_{0})$
,
 $B(S_{1},\unicode[STIX]{x1D70C}_{4})$
respectively.
$B(S_{1},\unicode[STIX]{x1D70C}_{4})$
respectively.
With this proposition and the previous theorem, we may now safely forget about the original function
![]() $\unicode[STIX]{x1D709}$
, and work now with
$\unicode[STIX]{x1D709}$
, and work now with
![]() $\unicode[STIX]{x1D709}^{\prime \prime }$
; the parameters
$\unicode[STIX]{x1D709}^{\prime \prime }$
; the parameters
![]() $a_{1},j$
will also no longer be relevant.
$a_{1},j$
will also no longer be relevant.
Proof. Let
![]() $\mathbf{n}$
,
$\mathbf{n}$
,
![]() $\mathbf{a}$
,
$\mathbf{a}$
,
![]() $\mathbf{a}_{(2)}$
be drawn independently and regularly from
$\mathbf{a}_{(2)}$
be drawn independently and regularly from
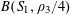 $B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
,
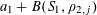 $a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
, and
$a_{1}+B(S_{1},\unicode[STIX]{x1D70C}_{2,j})$
, and
 $B(S_{1},\unicode[STIX]{x1D70C}_{2,j+2})$
respectively. From (9.58) we have
$B(S_{1},\unicode[STIX]{x1D70C}_{2,j+2})$
respectively. From (9.58) we have
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-\mathbf{n})-\unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})\Vert _{S}\ll \frac{1}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-\mathbf{n})-\unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})\Vert _{S}\ll \frac{1}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
with probability
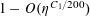 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
. Similarly, from (9.36), (9.37), (9.46) we see that with probability
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
. Similarly, from (9.36), (9.37), (9.46) we see that with probability
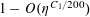 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
![]() $\mathbf{a}$
attains a value
$\mathbf{a}$
attains a value
![]() $a$
for which
$a$
for which
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(a-\mathbf{a}_{(2)}\in A_{(1)};\mathbf{a}_{(2)}\in A_{(2)};\Vert \unicode[STIX]{x1D709}^{\prime }(a)-\unicode[STIX]{x1D709}(a-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}\leqslant \frac{1}{\unicode[STIX]{x1D70C}_{3}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(a-\mathbf{a}_{(2)}\in A_{(1)};\mathbf{a}_{(2)}\in A_{(2)};\Vert \unicode[STIX]{x1D709}^{\prime }(a)-\unicode[STIX]{x1D709}(a-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}\leqslant \frac{1}{\unicode[STIX]{x1D70C}_{3}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}.\nonumber\end{eqnarray}$$
Using Lemma 4.4 to compare
![]() $\mathbf{a}$
and
$\mathbf{a}$
and
![]() $\mathbf{a}-\mathbf{n}$
, we also see that with probability
$\mathbf{a}-\mathbf{n}$
, we also see that with probability
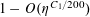 $1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
$1-O(\unicode[STIX]{x1D702}^{C_{1}/200})$
, the random variable
![]() $(\mathbf{a},\mathbf{n})$
attains a value
$(\mathbf{a},\mathbf{n})$
attains a value
![]() $(a,n)$
for which
$(a,n)$
for which
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(a-n-\mathbf{a}_{(2)}\in A_{(1)};\mathbf{a}_{(2)}\in A_{(2)};\nonumber\\ \displaystyle & & \displaystyle \qquad \Vert \unicode[STIX]{x1D709}^{\prime }(a-n)-\unicode[STIX]{x1D709}(a-n-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}\leqslant \frac{1}{\unicode[STIX]{x1D70C}_{3}}\biggr)\gg \unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathbb{P}\biggl(a-n-\mathbf{a}_{(2)}\in A_{(1)};\mathbf{a}_{(2)}\in A_{(2)};\nonumber\\ \displaystyle & & \displaystyle \qquad \Vert \unicode[STIX]{x1D709}^{\prime }(a-n)-\unicode[STIX]{x1D709}(a-n-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S}\leqslant \frac{1}{\unicode[STIX]{x1D70C}_{3}}\biggr)\gg \unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}.\nonumber\end{eqnarray}$$
From the union bound and Fubini’s theorem, we conclude that with probability
![]() $\gg \unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}$
, we simultaneously have the statements
$\gg \unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}$
, we simultaneously have the statements
 $$\begin{eqnarray}\displaystyle \mathbf{a}-\mathbf{n}-\mathbf{a}_{(2)} & \in & \displaystyle A_{(1)},\nonumber\\ \displaystyle \mathbf{a}_{(2)} & \in & \displaystyle A_{(2)},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-\mathbf{n})-\unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})\Vert _{S} & \ll & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-\mathbf{n})-\unicode[STIX]{x1D709}(\mathbf{a}-\mathbf{n}-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S} & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{a}-\mathbf{n}-\mathbf{a}_{(2)} & \in & \displaystyle A_{(1)},\nonumber\\ \displaystyle \mathbf{a}_{(2)} & \in & \displaystyle A_{(2)},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-\mathbf{n})-\unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})\Vert _{S} & \ll & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a}-\mathbf{n})-\unicode[STIX]{x1D709}(\mathbf{a}-\mathbf{n}-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})\Vert _{S} & {\leqslant} & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}}\nonumber\end{eqnarray}$$
and hence by the triangle inequality
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}(\mathbf{a}-\mathbf{n}-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})\Vert _{S}\ll \frac{1}{\unicode[STIX]{x1D70C}_{3}}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D709}^{\prime }(\mathbf{a})-\unicode[STIX]{x1D709}(\mathbf{a}-\mathbf{n}-\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}(\mathbf{a}_{(2)})-\unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})\Vert _{S}\ll \frac{1}{\unicode[STIX]{x1D70C}_{3}}.\end{eqnarray}$$
By the pigeonhole principle, we may thus find
 $a,a_{(2)}\in \mathbb{Z}/p\mathbb{Z}$
such that the statements
$a,a_{(2)}\in \mathbb{Z}/p\mathbb{Z}$
such that the statements
 $$\begin{eqnarray}\displaystyle a-\mathbf{n}-a_{(2)} & \in & \displaystyle A_{(1)},\nonumber\\ \displaystyle a_{(2)} & \in & \displaystyle A_{(2)},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(a)-\unicode[STIX]{x1D709}(a-\mathbf{n}-a_{(2)})-\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})\Vert _{S} & \ll & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a-\mathbf{n}-a_{(2)} & \in & \displaystyle A_{(1)},\nonumber\\ \displaystyle a_{(2)} & \in & \displaystyle A_{(2)},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime }(a)-\unicode[STIX]{x1D709}(a-\mathbf{n}-a_{(2)})-\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})\Vert _{S} & \ll & \displaystyle \frac{1}{\unicode[STIX]{x1D70C}_{3}}\nonumber\end{eqnarray}$$
simultaneously hold with probability
![]() $\gg \unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}$
, and thus with probability
$\gg \unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}$
, and thus with probability
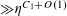 $\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}$
thanks to (9.46). Writing
$\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}$
thanks to (9.46). Writing
 $a_{0}:=a-a_{(2)}$
and
$a_{0}:=a-a_{(2)}$
and
 $\unicode[STIX]{x1D709}_{0}:=\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}^{\prime }(a)$
, and recalling from Theorem 9.7 that
$\unicode[STIX]{x1D709}_{0}:=\unicode[STIX]{x1D709}(a_{(2)})-\unicode[STIX]{x1D709}^{\prime }(a)$
, and recalling from Theorem 9.7 that
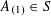 $A_{(1)}\in S$
, we thus have
$A_{(1)}\in S$
, we thus have
 $$\begin{eqnarray}\mathbb{P}(a_{0}-\mathbf{n}\in S;\Vert \unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})+\unicode[STIX]{x1D709}(a_{0}-\mathbf{n})-\unicode[STIX]{x1D709}_{0}\Vert _{S}\ll 1/\unicode[STIX]{x1D70C}_{3})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{P}(a_{0}-\mathbf{n}\in S;\Vert \unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})+\unicode[STIX]{x1D709}(a_{0}-\mathbf{n})-\unicode[STIX]{x1D709}_{0}\Vert _{S}\ll 1/\unicode[STIX]{x1D70C}_{3})\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
In particular, since
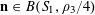 $\mathbf{n}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
and
$\mathbf{n}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
and
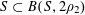 $S\subset B(S,2\unicode[STIX]{x1D70C}_{2})$
, we have
$S\subset B(S,2\unicode[STIX]{x1D70C}_{2})$
, we have
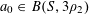 $a_{0}\in B(S,3\unicode[STIX]{x1D70C}_{2})$
.
$a_{0}\in B(S,3\unicode[STIX]{x1D70C}_{2})$
.
Let
![]() $\mathbf{n}_{0},\mathbf{n}_{1}$
be drawn independently and regularly from
$\mathbf{n}_{0},\mathbf{n}_{1}$
be drawn independently and regularly from
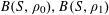 $B(S,\unicode[STIX]{x1D70C}_{0}),B(S,\unicode[STIX]{x1D70C}_{1})$
respectively, independently of all previous random variables. From the above estimate and (9.3), we see that with probability
$B(S,\unicode[STIX]{x1D70C}_{0}),B(S,\unicode[STIX]{x1D70C}_{1})$
respectively, independently of all previous random variables. From the above estimate and (9.3), we see that with probability
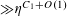 $\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}$
, the random variable
$\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}$
, the random variable
![]() $\mathbf{n}$
attains a value
$\mathbf{n}$
attains a value
![]() $n$
for which the statements
$n$
for which the statements
 $$\begin{eqnarray}\displaystyle & \displaystyle a_{0}-n\in S & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a_{0}-n\in S & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime \prime }(n)+\unicode[STIX]{x1D709}(a_{0}-n)-\unicode[STIX]{x1D709}_{0}\Vert _{S_{1}}\ll 1/\unicode[STIX]{x1D70C}_{3} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \Vert \unicode[STIX]{x1D709}^{\prime \prime }(n)+\unicode[STIX]{x1D709}(a_{0}-n)-\unicode[STIX]{x1D709}_{0}\Vert _{S_{1}}\ll 1/\unicode[STIX]{x1D70C}_{3} & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+a_{0}-n)\overline{f}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(a_{0}-n)\mathbf{n}_{1})|^{2}\geqslant \unicode[STIX]{x1D702}/8\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+a_{0}-n)\overline{f}(n_{0}+\mathbf{n}_{1})e_{p}(-\unicode[STIX]{x1D709}(a_{0}-n)\mathbf{n}_{1})|^{2}\geqslant \unicode[STIX]{x1D702}/8\end{eqnarray}$$
simultaneously hold.
Let
![]() $n$
obey the above estimates (9.60)–(9.62). If we now draw
$n$
obey the above estimates (9.60)–(9.62). If we now draw
![]() $\mathbf{h}$
regularly from
$\mathbf{h}$
regularly from
 $B(S_{1},\unicode[STIX]{x1D70C}_{4})$
, then by using Lemma 4.4 to compare
$B(S_{1},\unicode[STIX]{x1D70C}_{4})$
, then by using Lemma 4.4 to compare
![]() $\mathbf{n}_{1}$
with
$\mathbf{n}_{1}$
with
![]() $\mathbf{n}_{1}+\mathbf{h}$
in (9.62), we obtain
$\mathbf{n}_{1}+\mathbf{h}$
in (9.62), we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+\mathbf{n}_{1}+\mathbf{h})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}(-\unicode[STIX]{x1D709}(a_{0}-n)(\mathbf{n}_{1}+\mathbf{h}))|^{2}\gg \unicode[STIX]{x1D702}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+\mathbf{n}_{1}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+\mathbf{n}_{1}+\mathbf{h})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}(-\unicode[STIX]{x1D709}(a_{0}-n)(\mathbf{n}_{1}+\mathbf{h}))|^{2}\gg \unicode[STIX]{x1D702}\nonumber\end{eqnarray}$$
and thus by the triangle inequality in
![]() $L^{2}$
$L^{2}$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+n_{1}+\mathbf{h})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}(-\unicode[STIX]{x1D709}(a_{0}-n)(n_{1}+\mathbf{h}))|^{2}\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+n_{1}+\mathbf{h})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}(-\unicode[STIX]{x1D709}(a_{0}-n)(n_{1}+\mathbf{h}))|^{2}\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
We may delete the deterministic phase
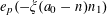 $e_{p}(-\unicode[STIX]{x1D709}(a_{0}-n)n_{1})$
to obtain
$e_{p}(-\unicode[STIX]{x1D709}(a_{0}-n)n_{1})$
to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+n_{1}+\mathbf{h})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}(-\unicode[STIX]{x1D709}(a_{0}-n)\mathbf{h})|^{2}\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+n_{1}+\mathbf{h})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}(-\unicode[STIX]{x1D709}(a_{0}-n)\mathbf{h})|^{2}\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
Since
![]() $\mathbf{h}$
takes values in
$\mathbf{h}$
takes values in
 $B(S_{1},\unicode[STIX]{x1D70C}_{4})$
, we see from (9.61) that
$B(S_{1},\unicode[STIX]{x1D70C}_{4})$
, we see from (9.61) that
 $$\begin{eqnarray}e_{p}(-\unicode[STIX]{x1D709}(a_{0}-\mathbf{n})\mathbf{h})=e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})-\unicode[STIX]{x1D709}_{0})\mathbf{h})+O(\unicode[STIX]{x1D702}^{100})\end{eqnarray}$$
$$\begin{eqnarray}e_{p}(-\unicode[STIX]{x1D709}(a_{0}-\mathbf{n})\mathbf{h})=e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(\mathbf{n})-\unicode[STIX]{x1D709}_{0})\mathbf{h})+O(\unicode[STIX]{x1D702}^{100})\end{eqnarray}$$
(for example), and so
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+n_{1}+\mathbf{h})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}_{0})\mathbf{h})|^{2}\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+n_{1}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+n_{1}+\mathbf{h})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}_{0})\mathbf{h})|^{2}\gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
Using Lemma 4.4 to compare
![]() $\mathbf{n}_{0}$
with
$\mathbf{n}_{0}$
with
![]() $\mathbf{n}_{0}+\mathbf{n}_{1}$
, we conclude that
$\mathbf{n}_{0}+\mathbf{n}_{1}$
, we conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+\mathbf{h})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}_{0})\mathbf{h})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+\mathbf{h})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}_{0})\mathbf{h})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}.\nonumber\end{eqnarray}$$
Multiplying by
 $\mathbb{P}(\mathbf{n}=n)$
and summing in
$\mathbb{P}(\mathbf{n}=n)$
and summing in
![]() $n$
, we obtain the claim. ◻
$n$
, we obtain the claim. ◻
9.17 Seventh step: derivatives of
 $f$
correlate with a locally bilinear form
$f$
correlate with a locally bilinear form
We now pass to the “cohomological” phase of the argument, in which we remove the error
 $\unicode[STIX]{x1D709}^{\prime \prime }(n+m)-\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}^{\prime \prime }(m)$
in the linearity of
$\unicode[STIX]{x1D709}^{\prime \prime }(n+m)-\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}^{\prime \prime }(m)$
in the linearity of
![]() $\unicode[STIX]{x1D709}^{\prime \prime }$
that appears in (9.57). This improved linearity of the form
$\unicode[STIX]{x1D709}^{\prime \prime }$
that appears in (9.57). This improved linearity of the form
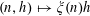 $(n,h)\mapsto \unicode[STIX]{x1D709}(n)h$
in the
$(n,h)\mapsto \unicode[STIX]{x1D709}(n)h$
in the
![]() $n$
aspect will come at the expense of the
$n$
aspect will come at the expense of the
![]() $h$
aspect, which will now merely be locally linear instead of globally linear. However, this is a worthwhile tradeoff for our purposes (and in any event local linearity is more natural in this context than global linearity).
$h$
aspect, which will now merely be locally linear instead of globally linear. However, this is a worthwhile tradeoff for our purposes (and in any event local linearity is more natural in this context than global linearity).
More precisely, the purpose of this subsection is to establish the following result towards the proof of Theorem 8.1.
Theorem 9.18. Let the notation and hypotheses be as in Theorem 8.1. Then there exists a set
![]() $S_{1}$
with
$S_{1}$
with
 $S\subset S_{1}\subset \mathbb{Z}/p\mathbb{Z}$
and
$S\subset S_{1}\subset \mathbb{Z}/p\mathbb{Z}$
and
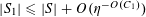 $|S_{1}|\leqslant |S|+O(\unicode[STIX]{x1D702}^{-O(C_{1})})$
, a locally bilinear map
$|S_{1}|\leqslant |S|+O(\unicode[STIX]{x1D702}^{-O(C_{1})})$
, a locally bilinear map
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}:B(S_{1},\unicode[STIX]{x1D70C}_{4})\times B(S_{1},\unicode[STIX]{x1D70C}_{4})\rightarrow \mathbb{R}/\mathbb{Z},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}:B(S_{1},\unicode[STIX]{x1D70C}_{4})\times B(S_{1},\unicode[STIX]{x1D70C}_{4})\rightarrow \mathbb{R}/\mathbb{Z},\end{eqnarray}$$
a shift
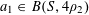 $a_{1}\in B(S,4\unicode[STIX]{x1D70C}_{2})$
, and a frequency
$a_{1}\in B(S,4\unicode[STIX]{x1D70C}_{2})$
, and a frequency
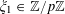 $\unicode[STIX]{x1D709}_{1}\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D709}_{1}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\biggl|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})e\biggl(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1})-\frac{\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1}}{p}\biggr)\biggr|^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \gg \,\unicode[STIX]{x1D702}^{C_{1}+O(1)}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\biggl|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})e\biggl(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1})-\frac{\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1}}{p}\biggr)\biggr|^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \gg \,\unicode[STIX]{x1D702}^{C_{1}+O(1)}\end{eqnarray}$$
if
 $\mathbf{n}_{0},\mathbf{m}_{1},\mathbf{n}_{1}$
are drawn independently and regularly from
$\mathbf{n}_{0},\mathbf{m}_{1},\mathbf{n}_{1}$
are drawn independently and regularly from
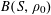 $B(S,\unicode[STIX]{x1D70C}_{0})$
,
$B(S,\unicode[STIX]{x1D70C}_{0})$
,
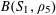 $B(S_{1},\unicode[STIX]{x1D70C}_{5})$
, and
$B(S_{1},\unicode[STIX]{x1D70C}_{5})$
, and
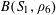 $B(S_{1},\unicode[STIX]{x1D70C}_{6})$
respectively.
$B(S_{1},\unicode[STIX]{x1D70C}_{6})$
respectively.
Once the proof of this theorem is completed, the auxiliary data
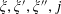 $\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709}^{\prime \prime },j$
,
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709}^{\prime \prime },j$
,
 $\unicode[STIX]{x1D6FA},\operatorname{VBQ}$
used in the previous parts of the section are no longer needed and may be discarded.
$\unicode[STIX]{x1D6FA},\operatorname{VBQ}$
used in the previous parts of the section are no longer needed and may be discarded.
We now prove Theorem 9.18. Let
![]() $j_{\ast },S_{1}$
be as in Theorem 9.9, let
$j_{\ast },S_{1}$
be as in Theorem 9.9, let
![]() $a_{\ast }$
,
$a_{\ast }$
,
![]() $\unicode[STIX]{x1D709}^{\prime }$
be as in Theorem 9.12, let
$\unicode[STIX]{x1D709}^{\prime }$
be as in Theorem 9.12, let
 $\unicode[STIX]{x1D709}^{\prime \prime }:B(S_{1},\unicode[STIX]{x1D70C}_{3})\rightarrow \mathbb{Z}/p\mathbb{Z}$
be as in Theorem 9.15, and let
$\unicode[STIX]{x1D709}^{\prime \prime }:B(S_{1},\unicode[STIX]{x1D70C}_{3})\rightarrow \mathbb{Z}/p\mathbb{Z}$
be as in Theorem 9.15, and let
![]() $a_{0},\unicode[STIX]{x1D709}_{0}$
be as in Proposition 9.16. We will use a “cohomological” argument to construct the required bilinear map
$a_{0},\unicode[STIX]{x1D709}_{0}$
be as in Proposition 9.16. We will use a “cohomological” argument to construct the required bilinear map
![]() $\unicode[STIX]{x1D6EF}$
. Namely, we define the cocycle
$\unicode[STIX]{x1D6EF}$
. Namely, we define the cocycle
 $\unicode[STIX]{x1D707}:B(S_{1},\unicode[STIX]{x1D70C}_{3}/2)\times B(S_{1},\unicode[STIX]{x1D70C}_{3}/2)\rightarrow \mathbb{Z}/p\mathbb{Z}$
to be the quantity
$\unicode[STIX]{x1D707}:B(S_{1},\unicode[STIX]{x1D70C}_{3}/2)\times B(S_{1},\unicode[STIX]{x1D70C}_{3}/2)\rightarrow \mathbb{Z}/p\mathbb{Z}$
to be the quantity
 $$\begin{eqnarray}\unicode[STIX]{x1D707}(n,m):=\unicode[STIX]{x1D709}^{\prime \prime }(n+m)-\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}^{\prime \prime }(m).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(n,m):=\unicode[STIX]{x1D709}^{\prime \prime }(n+m)-\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}^{\prime \prime }(m).\end{eqnarray}$$
Clearly (9.57) is symmetric, and we have the cocycle equation
 $$\begin{eqnarray}\unicode[STIX]{x1D707}(n_{1},n_{2}+n_{3})+\unicode[STIX]{x1D707}(n_{2},n_{3})=\unicode[STIX]{x1D707}(n_{1},n_{2})+\unicode[STIX]{x1D707}(n_{1}+n_{2},n_{3})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(n_{1},n_{2}+n_{3})+\unicode[STIX]{x1D707}(n_{2},n_{3})=\unicode[STIX]{x1D707}(n_{1},n_{2})+\unicode[STIX]{x1D707}(n_{1}+n_{2},n_{3})\end{eqnarray}$$
as well as the auxiliary equations
 $$\begin{eqnarray}\unicode[STIX]{x1D707}(n_{1},n_{2})=\unicode[STIX]{x1D707}(n_{2},n_{1});\qquad \unicode[STIX]{x1D707}(n_{1},0)=0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(n_{1},n_{2})=\unicode[STIX]{x1D707}(n_{2},n_{1});\qquad \unicode[STIX]{x1D707}(n_{1},0)=0\end{eqnarray}$$
whenever
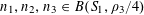 $n_{1},n_{2},n_{3}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
. From (9.57) we also have the estimate
$n_{1},n_{2},n_{3}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
. From (9.57) we also have the estimate
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D707}(n,m)\Vert _{S}\leqslant \frac{24}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D707}(n,m)\Vert _{S}\leqslant \frac{24}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
for all
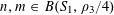 $n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
.
$n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
.
To construct the bilinear map
![]() $\unicode[STIX]{x1D6EF}$
, we will show that a certain projection of
$\unicode[STIX]{x1D6EF}$
, we will show that a certain projection of
![]() $\unicode[STIX]{x1D707}$
is a “coboundary” is a certain sense. Let
$\unicode[STIX]{x1D707}$
is a “coboundary” is a certain sense. Let
 $\unicode[STIX]{x1D719}:\mathbb{Z}^{S}\rightarrow \mathbb{Z}/p\mathbb{Z}$
be the homomorphism
$\unicode[STIX]{x1D719}:\mathbb{Z}^{S}\rightarrow \mathbb{Z}/p\mathbb{Z}$
be the homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D719}((n_{s})_{s\in S}):=\mathop{\sum }_{s\in S}n_{s}s.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}((n_{s})_{s\in S}):=\mathop{\sum }_{s\in S}n_{s}s.\end{eqnarray}$$
From (9.66), we see that for each
 $n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
we have a representation of the form
$n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
we have a representation of the form
 $$\begin{eqnarray}\unicode[STIX]{x1D707}(n,m)=\unicode[STIX]{x1D719}(\tilde{\unicode[STIX]{x1D707}}(n,m))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(n,m)=\unicode[STIX]{x1D719}(\tilde{\unicode[STIX]{x1D707}}(n,m))\end{eqnarray}$$
for some lift
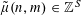 $\tilde{\unicode[STIX]{x1D707}}(n,m)\in \mathbb{Z}^{S}$
of size
$\tilde{\unicode[STIX]{x1D707}}(n,m)\in \mathbb{Z}^{S}$
of size
 $$\begin{eqnarray}|\tilde{\unicode[STIX]{x1D707}}(n,m)|\leqslant 24/\unicode[STIX]{x1D70C}_{3}.\end{eqnarray}$$
$$\begin{eqnarray}|\tilde{\unicode[STIX]{x1D707}}(n,m)|\leqslant 24/\unicode[STIX]{x1D70C}_{3}.\end{eqnarray}$$
This lift
![]() $\tilde{\unicode[STIX]{x1D707}}(n,m)$
is only defined up to an element of the kernel
$\tilde{\unicode[STIX]{x1D707}}(n,m)$
is only defined up to an element of the kernel
 $\text{ker}(\unicode[STIX]{x1D719}):=\{p\in \mathbb{Z}^{S}:\unicode[STIX]{x1D719}(p)=0\}$
of
$\text{ker}(\unicode[STIX]{x1D719}):=\{p\in \mathbb{Z}^{S}:\unicode[STIX]{x1D719}(p)=0\}$
of
![]() $\unicode[STIX]{x1D719}$
; to eliminate this ambiguity we will apply a projection. Since
$\unicode[STIX]{x1D719}$
; to eliminate this ambiguity we will apply a projection. Since
![]() $S$
contains a non-zero element,
$S$
contains a non-zero element,
 $\unicode[STIX]{x1D719}:\mathbb{Z}^{S}\rightarrow \mathbb{Z}/p\mathbb{Z}$
is a surjective homomorphism, and in particular,
$\unicode[STIX]{x1D719}:\mathbb{Z}^{S}\rightarrow \mathbb{Z}/p\mathbb{Z}$
is a surjective homomorphism, and in particular,
![]() $\text{ker}(\unicode[STIX]{x1D719})$
is a sublattice of
$\text{ker}(\unicode[STIX]{x1D719})$
is a sublattice of
![]() $\mathbb{Z}^{S}$
of index
$\mathbb{Z}^{S}$
of index
![]() $p$
. Applying Lemma 4.8, we may find generators
$p$
. Applying Lemma 4.8, we may find generators
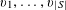 $v_{1},\ldots ,v_{|S|}$
of
$v_{1},\ldots ,v_{|S|}$
of
![]() $\text{ker}(\unicode[STIX]{x1D719})$
and real numbers
$\text{ker}(\unicode[STIX]{x1D719})$
and real numbers
 $N_{1},\ldots ,N_{|S|}>0$
with
$N_{1},\ldots ,N_{|S|}>0$
with
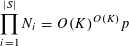 $$\begin{eqnarray}\mathop{\prod }_{i=1}^{|S|}N_{i}=O(K)^{O(K)}p\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{i=1}^{|S|}N_{i}=O(K)^{O(K)}p\end{eqnarray}$$
such that
 $$\begin{eqnarray}\displaystyle B_{\mathbb{R}^{S}}(0,O(K)^{-3K/2}t)\cap \text{ker}(\unicode[STIX]{x1D719}) & \subset & \displaystyle \{n_{1}v_{1}+\cdots +n_{|S|}v_{|S|}:|n_{i}|\leqslant tN_{i}\}\nonumber\\ \displaystyle & \subset & \displaystyle B_{\mathbb{R}^{S}}(0,t)\cap \text{ker}(\unicode[STIX]{x1D719})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B_{\mathbb{R}^{S}}(0,O(K)^{-3K/2}t)\cap \text{ker}(\unicode[STIX]{x1D719}) & \subset & \displaystyle \{n_{1}v_{1}+\cdots +n_{|S|}v_{|S|}:|n_{i}|\leqslant tN_{i}\}\nonumber\\ \displaystyle & \subset & \displaystyle B_{\mathbb{R}^{S}}(0,t)\cap \text{ker}(\unicode[STIX]{x1D719})\end{eqnarray}$$
for all
![]() $t>0$
.
$t>0$
.
By relabelling, we may take the
![]() $N_{i}$
to be non-increasing. Let
$N_{i}$
to be non-increasing. Let
![]() $d$
,
$d$
,
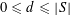 $0\leqslant d\leqslant |S|$
be such that
$0\leqslant d\leqslant |S|$
be such that
 $$\begin{eqnarray}N_{1}\geqslant \cdots \geqslant N_{d}>\frac{\unicode[STIX]{x1D70C}_{3}}{\exp (K^{C_{1}})}\geqslant N_{d+1}\geqslant \cdots \geqslant N_{|S|}.\end{eqnarray}$$
$$\begin{eqnarray}N_{1}\geqslant \cdots \geqslant N_{d}>\frac{\unicode[STIX]{x1D70C}_{3}}{\exp (K^{C_{1}})}\geqslant N_{d+1}\geqslant \cdots \geqslant N_{|S|}.\end{eqnarray}$$
From (9.69), (8.3) we see that
![]() $d$
cannot equal
$d$
cannot equal
![]() $|S|$
. Let
$|S|$
. Let
![]() $V$
be the
$V$
be the
![]() $d$
-dimensional subspace of
$d$
-dimensional subspace of
![]() $\mathbb{R}^{S}$
spanned by
$\mathbb{R}^{S}$
spanned by
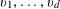 $v_{1},\ldots ,v_{d}$
, let
$v_{1},\ldots ,v_{d}$
, let
![]() $V^{\bot }$
be the orthogonal complement of
$V^{\bot }$
be the orthogonal complement of
![]() $V$
in
$V$
in
![]() $\mathbb{R}^{S}$
, and let
$\mathbb{R}^{S}$
, and let
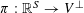 $\unicode[STIX]{x1D70B}:\mathbb{R}^{S}\rightarrow V^{\bot }$
be the orthogonal projection.
$\unicode[STIX]{x1D70B}:\mathbb{R}^{S}\rightarrow V^{\bot }$
be the orthogonal projection.
We claim that
 $\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n,m))$
is now uniquely determined by
$\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n,m))$
is now uniquely determined by
![]() $\unicode[STIX]{x1D707}(n,m)$
for
$\unicode[STIX]{x1D707}(n,m)$
for
 $n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
. Indeed, if
$n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
. Indeed, if
![]() $\tilde{\unicode[STIX]{x1D707}}(n,m)$
and
$\tilde{\unicode[STIX]{x1D707}}(n,m)$
and
 $\tilde{\unicode[STIX]{x1D707}}^{\prime }(n,m)$
both obeyed (9.67), (9.68), then their difference (call it
$\tilde{\unicode[STIX]{x1D707}}^{\prime }(n,m)$
both obeyed (9.67), (9.68), then their difference (call it
![]() $w$
) would be of magnitude
$w$
) would be of magnitude
 $O(1/\unicode[STIX]{x1D70C}_{3})$
and lies in the kernel of
$O(1/\unicode[STIX]{x1D70C}_{3})$
and lies in the kernel of
![]() $\unicode[STIX]{x1D719}$
. By (9.70) with
$\unicode[STIX]{x1D719}$
. By (9.70) with
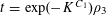 $t=\exp (-K^{C_{1}})\unicode[STIX]{x1D70C}_{3}$
, we conclude that
$t=\exp (-K^{C_{1}})\unicode[STIX]{x1D70C}_{3}$
, we conclude that
![]() $w$
lies in
$w$
lies in
![]() $V$
, and hence
$V$
, and hence
 $\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n,m))$
and
$\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n,m))$
and
 $\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}^{\prime }(n,m))$
agree.
$\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}^{\prime }(n,m))$
agree.
A variant of the above argument shows that
![]() $\unicode[STIX]{x1D70B}\circ \tilde{\unicode[STIX]{x1D707}}$
also continues to obey the cocycle equation.
$\unicode[STIX]{x1D70B}\circ \tilde{\unicode[STIX]{x1D707}}$
also continues to obey the cocycle equation.
Lemma 9.19 (Projected lift is a cocycle).
One has
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}+n_{3}))+\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{2},n_{3}))=\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))+\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1}+n_{2},n_{3}))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}+n_{3}))+\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{2},n_{3}))=\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))+\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1}+n_{2},n_{3}))\end{eqnarray}$$
and additionally
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))=\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{2},n_{1}));\qquad \unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},0))=0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))=\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{2},n_{1}));\qquad \unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},0))=0\end{eqnarray}$$
for all
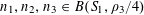 $n_{1},n_{2},n_{3}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
.
$n_{1},n_{2},n_{3}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
.
Proof. By (9.68), the quantity
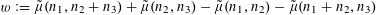 $w:=\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}+n_{3})+\tilde{\unicode[STIX]{x1D707}}(n_{2},n_{3})-\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2})-\tilde{\unicode[STIX]{x1D707}}(n_{1}+n_{2},n_{3})$
has magnitude
$w:=\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}+n_{3})+\tilde{\unicode[STIX]{x1D707}}(n_{2},n_{3})-\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2})-\tilde{\unicode[STIX]{x1D707}}(n_{1}+n_{2},n_{3})$
has magnitude
 $O(1/\unicode[STIX]{x1D70C}_{3})$
; by (9.67), (9.65),
$O(1/\unicode[STIX]{x1D70C}_{3})$
; by (9.67), (9.65),
![]() $w$
lies in the kernel of
$w$
lies in the kernel of
![]() $\unicode[STIX]{x1D719}$
. Repeating the previous arguments, we conclude that
$\unicode[STIX]{x1D719}$
. Repeating the previous arguments, we conclude that
![]() $w\in V$
. Applying the homomorphism
$w\in V$
. Applying the homomorphism
![]() $\unicode[STIX]{x1D70B}$
, we obtain the first claim. The second claim is proven similarly.◻
$\unicode[STIX]{x1D70B}$
, we obtain the first claim. The second claim is proven similarly.◻
We can in fact make
![]() $\unicode[STIX]{x1D70B}\circ \tilde{\unicode[STIX]{x1D707}}$
a coboundary, after shrinking the domain somewhat.
$\unicode[STIX]{x1D70B}\circ \tilde{\unicode[STIX]{x1D707}}$
a coboundary, after shrinking the domain somewhat.
Proposition 9.20 (Projected lift is a coboundary).
There exists a map
 $F:B(S_{1},2\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C}_{3})\rightarrow V^{\bot }$
with
$F:B(S_{1},2\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C}_{3})\rightarrow V^{\bot }$
with
 $$\begin{eqnarray}F(n)\ll \frac{K^{O(C_{1})}}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
$$\begin{eqnarray}F(n)\ll \frac{K^{O(C_{1})}}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
for all
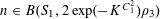 $n\in B(S_{1},2\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C}_{3})$
, such that
$n\in B(S_{1},2\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C}_{3})$
, such that
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))=F(n_{1}+n_{2})-F(n_{1})-F(n_{2})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))=F(n_{1}+n_{2})-F(n_{1})-F(n_{2})\end{eqnarray}$$
for all
 $n_{1},n_{2}\in B(S_{1},\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C}_{3})$
.
$n_{1},n_{2}\in B(S_{1},\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C}_{3})$
.
Proof. As a first attempt at constructing
![]() $F$
, we introduce the average
$F$
, we introduce the average
 $$\begin{eqnarray}F_{1}(n):=\mathbb{E}\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n,\mathbf{n}_{3}))\end{eqnarray}$$
$$\begin{eqnarray}F_{1}(n):=\mathbb{E}\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n,\mathbf{n}_{3}))\end{eqnarray}$$
for
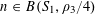 $n\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
, where
$n\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
, where
![]() $\mathbf{n}_{3}$
is drawn regularly from
$\mathbf{n}_{3}$
is drawn regularly from
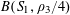 $B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
. From (9.68) we have
$B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
. From (9.68) we have
 $$\begin{eqnarray}|F_{1}(n)|\leqslant \frac{24}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
$$\begin{eqnarray}|F_{1}(n)|\leqslant \frac{24}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
for all
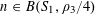 $n\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
. Also, since
$n\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
. Also, since
 $|S_{1}|\ll K^{O(C_{1})}$
, if we replace
$|S_{1}|\ll K^{O(C_{1})}$
, if we replace
![]() $n_{3}$
by
$n_{3}$
by
![]() $\mathbf{n}_{3}$
in Lemma 9.19 and take expectations using Lemma 4.4, we conclude that
$\mathbf{n}_{3}$
in Lemma 9.19 and take expectations using Lemma 4.4, we conclude that
 $$\begin{eqnarray}F_{1}(n_{1})+F_{1}(n_{2})=\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))+F_{1}(n_{1}+n_{2})+O\biggl(\frac{K^{O(C_{1})}\Vert n_{2}\Vert _{S_{1}^{\bot }}}{\unicode[STIX]{x1D70C}_{3}^{2}}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}F_{1}(n_{1})+F_{1}(n_{2})=\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))+F_{1}(n_{1}+n_{2})+O\biggl(\frac{K^{O(C_{1})}\Vert n_{2}\Vert _{S_{1}^{\bot }}}{\unicode[STIX]{x1D70C}_{3}^{2}}\biggr)\end{eqnarray}$$
for all
 $n_{1},n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/8)$
.
$n_{1},n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/8)$
.
If we now introduce the modified cocycle
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1},n_{2}):=\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))+F_{1}(n_{1}+n_{2})-F_{1}(n_{1})-F_{1}(n_{2})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1},n_{2}):=\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))+F_{1}(n_{1}+n_{2})-F_{1}(n_{1})-F_{1}(n_{2})\end{eqnarray}$$
for
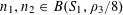 $n_{1},n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/8)$
, then we have the cocycle equation
$n_{1},n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/8)$
, then we have the cocycle equation
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1},n_{2}+n_{3})+\unicode[STIX]{x1D70E}_{1}(n_{2},n_{3})=\unicode[STIX]{x1D70E}_{1}(n_{1},n_{2})+\unicode[STIX]{x1D70E}_{1}(n_{1}+n_{2},n_{3}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1},n_{2}+n_{3})+\unicode[STIX]{x1D70E}_{1}(n_{2},n_{3})=\unicode[STIX]{x1D70E}_{1}(n_{1},n_{2})+\unicode[STIX]{x1D70E}_{1}(n_{1}+n_{2},n_{3}),\end{eqnarray}$$
the auxiliary equations
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1},n_{2})=\unicode[STIX]{x1D70E}_{1}(n_{2},n_{1});\qquad \unicode[STIX]{x1D70E}_{1}(n_{1},0)=0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1},n_{2})=\unicode[STIX]{x1D70E}_{1}(n_{2},n_{1});\qquad \unicode[STIX]{x1D70E}_{1}(n_{1},0)=0\end{eqnarray}$$
and the bound
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1},n_{2})\ll \frac{K^{O(C_{1})}\Vert n_{2}\Vert _{S_{1}^{\bot }}}{\unicode[STIX]{x1D70C}_{3}^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1},n_{2})\ll \frac{K^{O(C_{1})}\Vert n_{2}\Vert _{S_{1}^{\bot }}}{\unicode[STIX]{x1D70C}_{3}^{2}}\end{eqnarray}$$
for
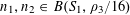 $n_{1},n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/16)$
.
$n_{1},n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/16)$
.
We now make
![]() $\unicode[STIX]{x1D70E}_{1}$
a coboundary by using a basis for
$\unicode[STIX]{x1D70E}_{1}$
a coboundary by using a basis for
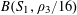 $B(S_{1},\unicode[STIX]{x1D70C}_{3}/16)$
. Set
$B(S_{1},\unicode[STIX]{x1D70C}_{3}/16)$
. Set
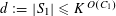 $d:=|S_{1}|\leqslant K^{O(C_{1})}$
. By Corollary 4.9, we can find
$d:=|S_{1}|\leqslant K^{O(C_{1})}$
. By Corollary 4.9, we can find
 $a_{1},\ldots ,a_{d}$
of
$a_{1},\ldots ,a_{d}$
of
![]() $\mathbb{Z}/p\mathbb{Z}$
and real numbers
$\mathbb{Z}/p\mathbb{Z}$
and real numbers
 $N_{1},\ldots ,N_{d}>0$
such that
$N_{1},\ldots ,N_{d}>0$
such that
 $$\begin{eqnarray}\Vert a_{i}\Vert _{S_{1}^{\bot }}\leqslant N_{i}^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\Vert a_{i}\Vert _{S_{1}^{\bot }}\leqslant N_{i}^{-1}\end{eqnarray}$$
for all
 $i=1,\ldots ,d$
, and such that for any
$i=1,\ldots ,d$
, and such that for any
 $a\in \mathbb{Z}/p\mathbb{Z}$
, there exists a representation
$a\in \mathbb{Z}/p\mathbb{Z}$
, there exists a representation
 $$\begin{eqnarray}a=m_{1}a_{1}+\cdots +m_{d}a_{d}\end{eqnarray}$$
$$\begin{eqnarray}a=m_{1}a_{1}+\cdots +m_{d}a_{d}\end{eqnarray}$$
with
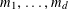 $m_{1},\ldots ,m_{d}$
integers of size
$m_{1},\ldots ,m_{d}$
integers of size
 $$\begin{eqnarray}m_{i}\ll \exp (O(K^{O(C_{1})}))N_{i}\Vert a\Vert _{S_{1}^{\bot }}\end{eqnarray}$$
$$\begin{eqnarray}m_{i}\ll \exp (O(K^{O(C_{1})}))N_{i}\Vert a\Vert _{S_{1}^{\bot }}\end{eqnarray}$$
for
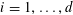 $i=1,\ldots ,d$
, with at most one such representation obeying the bounds
$i=1,\ldots ,d$
, with at most one such representation obeying the bounds
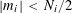 $|m_{i}|<N_{i}/2$
for
$|m_{i}|<N_{i}/2$
for
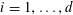 $i=1,\ldots ,d$
.
$i=1,\ldots ,d$
.
By relabelling we may assume that
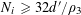 $N_{i}\geqslant 32d^{\prime }/\unicode[STIX]{x1D70C}_{3}$
for
$N_{i}\geqslant 32d^{\prime }/\unicode[STIX]{x1D70C}_{3}$
for
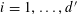 $i=1,\ldots ,d^{\prime }$
and
$i=1,\ldots ,d^{\prime }$
and
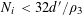 $N_{i}<32d^{\prime }/\unicode[STIX]{x1D70C}_{3}$
for
$N_{i}<32d^{\prime }/\unicode[STIX]{x1D70C}_{3}$
for
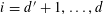 $i=d^{\prime }+1,\ldots ,d$
for some
$i=d^{\prime }+1,\ldots ,d$
for some
 $0\leqslant d^{\prime }\leqslant d$
. By (9.75) we have
$0\leqslant d^{\prime }\leqslant d$
. By (9.75) we have
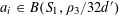 $a_{i}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/32d^{\prime })$
for all
$a_{i}\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/32d^{\prime })$
for all
 $i=1,\ldots ,d^{\prime }$
. In particular, from (9.73) we see that for any
$i=1,\ldots ,d^{\prime }$
. In particular, from (9.73) we see that for any
 $n\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/32)$
and
$n\in B(S_{1},\unicode[STIX]{x1D70C}_{3}/32)$
and
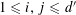 $1\leqslant i,j\leqslant d^{\prime }$
, we have
$1\leqslant i,j\leqslant d^{\prime }$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1},a_{i}+a_{j})+\unicode[STIX]{x1D70E}_{1}(a_{i},a_{j})=\unicode[STIX]{x1D70E}_{1}(n_{1},a_{i})+\unicode[STIX]{x1D70E}_{1}(n_{1}+a_{i},a_{j})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1},a_{i}+a_{j})+\unicode[STIX]{x1D70E}_{1}(a_{i},a_{j})=\unicode[STIX]{x1D70E}_{1}(n_{1},a_{i})+\unicode[STIX]{x1D70E}_{1}(n_{1}+a_{i},a_{j})\end{eqnarray}$$
and hence by swapping
![]() $i$
and
$i$
and
![]() $j$
and subtracting
$j$
and subtracting
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1}+a_{j},a_{i})-\unicode[STIX]{x1D70E}_{1}(n_{1},a_{i})=\unicode[STIX]{x1D70E}_{1}(n_{1}+a_{i},a_{j})-\unicode[STIX]{x1D70E}_{1}(n_{1},a_{j}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n_{1}+a_{j},a_{i})-\unicode[STIX]{x1D70E}_{1}(n_{1},a_{i})=\unicode[STIX]{x1D70E}_{1}(n_{1}+a_{i},a_{j})-\unicode[STIX]{x1D70E}_{1}(n_{1},a_{j}).\end{eqnarray}$$
Let
![]() $P\subset \mathbb{Z}^{d^{\prime }}$
denote the collection of tuples
$P\subset \mathbb{Z}^{d^{\prime }}$
denote the collection of tuples
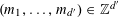 $(m_{1},\ldots ,m_{d^{\prime }})\in \mathbb{Z}^{d^{\prime }}$
with
$(m_{1},\ldots ,m_{d^{\prime }})\in \mathbb{Z}^{d^{\prime }}$
with
 $|m_{i}|\leqslant \unicode[STIX]{x1D70C}_{3}/2N_{i}$
for
$|m_{i}|\leqslant \unicode[STIX]{x1D70C}_{3}/2N_{i}$
for
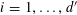 $i=1,\ldots ,d^{\prime }$
, and for each
$i=1,\ldots ,d^{\prime }$
, and for each
![]() $m\in P$
and
$m\in P$
and
 $i=1,\ldots ,d$
, define the quantity
$i=1,\ldots ,d$
, define the quantity
 $$\begin{eqnarray}f_{i}(m):=\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D719}(m),a_{i})\end{eqnarray}$$
$$\begin{eqnarray}f_{i}(m):=\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D719}(m),a_{i})\end{eqnarray}$$
where
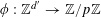 $\unicode[STIX]{x1D719}:\mathbb{Z}^{d^{\prime }}\rightarrow \mathbb{Z}/p\mathbb{Z}$
is the homomorphism
$\unicode[STIX]{x1D719}:\mathbb{Z}^{d^{\prime }}\rightarrow \mathbb{Z}/p\mathbb{Z}$
is the homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D719}(m_{1},\ldots ,m_{d^{\prime }}):=\mathop{\sum }_{k=1}^{d^{\prime }}m_{k}a_{k}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}(m_{1},\ldots ,m_{d^{\prime }}):=\mathop{\sum }_{k=1}^{d^{\prime }}m_{k}a_{k}.\end{eqnarray}$$
Then from (9.75) we have
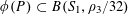 $\unicode[STIX]{x1D719}(P)\subset B(S_{1},\unicode[STIX]{x1D70C}_{3}/32)$
. The above identity then says that the “
$\unicode[STIX]{x1D719}(P)\subset B(S_{1},\unicode[STIX]{x1D70C}_{3}/32)$
. The above identity then says that the “
![]() $1$
-form”
$1$
-form”
 $(f_{1},\ldots ,f_{d^{\prime }})$
is “closed” or “curl-free” in the sense that
$(f_{1},\ldots ,f_{d^{\prime }})$
is “closed” or “curl-free” in the sense that
 $$\begin{eqnarray}f_{i}(m+e_{j})-f_{i}(m)=f_{j}(m+e_{i})-f_{j}(m)\end{eqnarray}$$
$$\begin{eqnarray}f_{i}(m+e_{j})-f_{i}(m)=f_{j}(m+e_{i})-f_{j}(m)\end{eqnarray}$$
whenever
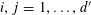 $i,j=1,\ldots ,d^{\prime }$
and
$i,j=1,\ldots ,d^{\prime }$
and
 $m,m+e_{i},m+e_{j}\in P$
, where
$m,m+e_{i},m+e_{j}\in P$
, where
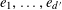 $e_{1},\ldots ,e_{d^{\prime }}$
is the standard basis for
$e_{1},\ldots ,e_{d^{\prime }}$
is the standard basis for
![]() $P$
. This implies that there exists a function
$P$
. This implies that there exists a function
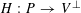 $H:P\rightarrow V^{\bot }$
such that
$H:P\rightarrow V^{\bot }$
such that
 $F(0)=0$
and
$F(0)=0$
and
 $f_{i}(m)=H(m+e_{i})-H(m)$
whenever
$f_{i}(m)=H(m+e_{i})-H(m)$
whenever
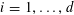 $i=1,\ldots ,d$
and
$i=1,\ldots ,d$
and
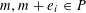 $m,m+e_{i}\in P$
. Indeed, one can define
$m,m+e_{i}\in P$
. Indeed, one can define
![]() $H$
to be an “antiderivative” of the
$H$
to be an “antiderivative” of the
 $(f_{1},\ldots ,f_{d^{\prime }})$
by setting
$(f_{1},\ldots ,f_{d^{\prime }})$
by setting
 $$\begin{eqnarray}H(m):=\mathop{\sum }_{l=0}^{L-1}f_{i_{l}}(m_{l})\end{eqnarray}$$
$$\begin{eqnarray}H(m):=\mathop{\sum }_{l=0}^{L-1}f_{i_{l}}(m_{l})\end{eqnarray}$$
whenever
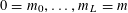 $0=m_{0},\ldots ,m_{L}=m$
is a path in
$0=m_{0},\ldots ,m_{L}=m$
is a path in
![]() $P$
with
$P$
with
 $m_{l+1}=m_{l}+e_{i_{l}}$
for
$m_{l+1}=m_{l}+e_{i_{l}}$
for
 $l=0,\ldots ,L-1$
; a “homotopy” argument using (9.78) shows that the right-hand side does not depend on the choice of path. From (9.74), (9.75) we have
$l=0,\ldots ,L-1$
; a “homotopy” argument using (9.78) shows that the right-hand side does not depend on the choice of path. From (9.74), (9.75) we have
 $$\begin{eqnarray}f_{i}(m)\ll \frac{K^{O(C_{1})}}{N_{i}\unicode[STIX]{x1D70C}_{3}^{2}}\end{eqnarray}$$
$$\begin{eqnarray}f_{i}(m)\ll \frac{K^{O(C_{1})}}{N_{i}\unicode[STIX]{x1D70C}_{3}^{2}}\end{eqnarray}$$
for
![]() $m\in P$
and
$m\in P$
and
 $i=1,\ldots ,d^{\prime }$
, which on “integrating” (and recalling that
$i=1,\ldots ,d^{\prime }$
, which on “integrating” (and recalling that
 $d^{\prime }\leqslant d\ll K^{O(C_{1})}$
) implies that
$d^{\prime }\leqslant d\ll K^{O(C_{1})}$
) implies that
 $$\begin{eqnarray}H(m)\ll \frac{K^{O(C_{1})}}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
$$\begin{eqnarray}H(m)\ll \frac{K^{O(C_{1})}}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
for all
![]() $m\in P$
.
$m\in P$
.
Since
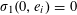 $\unicode[STIX]{x1D70E}_{1}(0,e_{i})=0$
, we have
$\unicode[STIX]{x1D70E}_{1}(0,e_{i})=0$
, we have
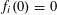 $f_{i}(0)=0$
and hence
$f_{i}(0)=0$
and hence
 $H(e_{i})=0$
for all
$H(e_{i})=0$
for all
 $i=1,\ldots ,d^{\prime }$
. Thus we have
$i=1,\ldots ,d^{\prime }$
. Thus we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D719}(m),\unicode[STIX]{x1D719}(e_{i}))=H(m+e_{i})-H(m)-H(e_{i})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D719}(m),\unicode[STIX]{x1D719}(e_{i}))=H(m+e_{i})-H(m)-H(e_{i})\end{eqnarray}$$
whenever
 $m,m+e_{i}\in P$
. An induction (on the magnitude of a vector
$m,m+e_{i}\in P$
. An induction (on the magnitude of a vector
![]() $m^{\prime }$
) using (9.73) then shows that
$m^{\prime }$
) using (9.73) then shows that
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D719}(m),\unicode[STIX]{x1D719}(m^{\prime }))=H(m+m^{\prime })-H(m)-H(m^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(\unicode[STIX]{x1D719}(m),\unicode[STIX]{x1D719}(m^{\prime }))=H(m+m^{\prime })-H(m)-H(m^{\prime })\end{eqnarray}$$
whenever
 $m,m^{\prime },m+m^{\prime }\in P$
. Now, if
$m,m^{\prime },m+m^{\prime }\in P$
. Now, if
 $n\in B(S_{1},2\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C})$
, then by (9.76), (9.77) we see that
$n\in B(S_{1},2\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C})$
, then by (9.76), (9.77) we see that
 $n=\unicode[STIX]{x1D719}(m)$
for some
$n=\unicode[STIX]{x1D719}(m)$
for some
![]() $m\in P$
. If we then define
$m\in P$
. If we then define
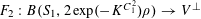 $F_{2}:B(S_{1},2\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C})\rightarrow V^{\bot }$
by setting
$F_{2}:B(S_{1},2\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C})\rightarrow V^{\bot }$
by setting
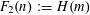 $F_{2}(n):=H(m)$
, we conclude that
$F_{2}(n):=H(m)$
, we conclude that
 $$\begin{eqnarray}F_{2}(n)\ll \frac{K^{O(C_{1})}}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
$$\begin{eqnarray}F_{2}(n)\ll \frac{K^{O(C_{1})}}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n,n^{\prime })=F_{2}(n+n^{\prime })-F_{2}(n)-F_{2}(n^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}(n,n^{\prime })=F_{2}(n+n^{\prime })-F_{2}(n)-F_{2}(n^{\prime })\end{eqnarray}$$
for all
 $n,n^{\prime }\in B(S_{1},\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C})$
. Setting
$n,n^{\prime }\in B(S_{1},\exp (-K^{C_{1}^{2}})\unicode[STIX]{x1D70C})$
. Setting
 $F:=F_{2}-F_{1}$
, we obtain the claim.◻
$F:=F_{2}-F_{1}$
, we obtain the claim.◻
Let
![]() $F$
be as in Proposition 9.20. We use
$F$
be as in Proposition 9.20. We use
![]() $F$
to construct the locally bilinear form
$F$
to construct the locally bilinear form
 $\unicode[STIX]{x1D6EF}:B(S_{1},\unicode[STIX]{x1D70C}_{4})\times B(S_{1},\unicode[STIX]{x1D70C}_{4})\rightarrow \mathbb{R}/\mathbb{Z}$
as follows. We first define the locally linear map
$\unicode[STIX]{x1D6EF}:B(S_{1},\unicode[STIX]{x1D70C}_{4})\times B(S_{1},\unicode[STIX]{x1D70C}_{4})\rightarrow \mathbb{R}/\mathbb{Z}$
as follows. We first define the locally linear map
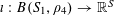 $\unicode[STIX]{x1D704}:B(S_{1},\unicode[STIX]{x1D70C}_{4})\rightarrow \mathbb{R}^{S}$
by the formula
$\unicode[STIX]{x1D704}:B(S_{1},\unicode[STIX]{x1D70C}_{4})\rightarrow \mathbb{R}^{S}$
by the formula
 $$\begin{eqnarray}\unicode[STIX]{x1D704}(m):=\biggl(\biggl\{\frac{ms}{p}\biggr\}\biggr)_{s\in S},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}(m):=\biggl(\biggl\{\frac{ms}{p}\biggr\}\biggr)_{s\in S},\end{eqnarray}$$
where
 $x\mapsto \{x\}$
is the signed fractional map from
$x\mapsto \{x\}$
is the signed fractional map from
![]() $\mathbb{R}/\mathbb{Z}$
to
$\mathbb{R}/\mathbb{Z}$
to
 $(-1/2,1/2]$
; note that
$(-1/2,1/2]$
; note that
![]() $\unicode[STIX]{x1D704}$
takes values in the box
$\unicode[STIX]{x1D704}$
takes values in the box
 $[-\unicode[STIX]{x1D70C}_{4},\unicode[STIX]{x1D70C}_{4}]^{S}$
. We then define
$[-\unicode[STIX]{x1D70C}_{4},\unicode[STIX]{x1D70C}_{4}]^{S}$
. We then define
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}(n,m):=\frac{\unicode[STIX]{x1D709}^{\prime \prime }(n)m}{p}-F(n)\cdot \unicode[STIX]{x1D704}(m)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}(n,m):=\frac{\unicode[STIX]{x1D709}^{\prime \prime }(n)m}{p}-F(n)\cdot \unicode[STIX]{x1D704}(m)\end{eqnarray}$$
for
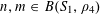 $n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{4})$
, where
$n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{4})$
, where
![]() $\cdot$
denotes the dot product on
$\cdot$
denotes the dot product on
![]() $\mathbb{R}^{S}$
. It is clear that
$\mathbb{R}^{S}$
. It is clear that
![]() $\unicode[STIX]{x1D6EF}$
is locally linear in
$\unicode[STIX]{x1D6EF}$
is locally linear in
![]() $m$
; we also claim that it is locally linear in
$m$
; we also claim that it is locally linear in
![]() $n$
, thus
$n$
, thus
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}(n_{1}+n_{2},m)-\unicode[STIX]{x1D6EF}(n_{1},m)-\unicode[STIX]{x1D6EF}(n_{2},m)=0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}(n_{1}+n_{2},m)-\unicode[STIX]{x1D6EF}(n_{1},m)-\unicode[STIX]{x1D6EF}(n_{2},m)=0\end{eqnarray}$$
whenever
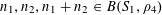 $n_{1},n_{2},n_{1}+n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{4})$
. By (9.64) and Proposition 9.20, the left-hand side of (9.80) may be written as
$n_{1},n_{2},n_{1}+n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{4})$
. By (9.64) and Proposition 9.20, the left-hand side of (9.80) may be written as
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}(n_{1},n_{2})m}{p}-\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))\cdot \unicode[STIX]{x1D704}(m)~\text{mod}~1.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}(n_{1},n_{2})m}{p}-\unicode[STIX]{x1D70B}(\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2}))\cdot \unicode[STIX]{x1D704}(m)~\text{mod}~1.\end{eqnarray}$$
From (9.67) we have
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}(n_{1},n_{2})m}{p}=\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2})\cdot \unicode[STIX]{x1D704}(m)~\text{mod}~1\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}(n_{1},n_{2})m}{p}=\tilde{\unicode[STIX]{x1D707}}(n_{1},n_{2})\cdot \unicode[STIX]{x1D704}(m)~\text{mod}~1\end{eqnarray}$$
so to prove (9.80), it suffices to show that
![]() $\unicode[STIX]{x1D704}(m)$
lies in
$\unicode[STIX]{x1D704}(m)$
lies in
![]() $V^{\bot }$
. This is equivalent to showing that
$V^{\bot }$
. This is equivalent to showing that
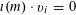 $\unicode[STIX]{x1D704}(m)\cdot v_{i}=0$
for
$\unicode[STIX]{x1D704}(m)\cdot v_{i}=0$
for
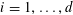 $i=1,\ldots ,d$
. Since
$i=1,\ldots ,d$
. Since
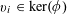 $v_{i}\in \text{ker}(\unicode[STIX]{x1D719})$
, we have
$v_{i}\in \text{ker}(\unicode[STIX]{x1D719})$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D704}(m)\cdot v_{i}=0~\text{mod}~1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}(m)\cdot v_{i}=0~\text{mod}~1.\end{eqnarray}$$
On the other hand, we have
 $\unicode[STIX]{x1D704}(m)=O(K^{1/2}\unicode[STIX]{x1D70C}_{4})$
, and from (9.70) with
$\unicode[STIX]{x1D704}(m)=O(K^{1/2}\unicode[STIX]{x1D70C}_{4})$
, and from (9.70) with
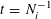 $t=N_{i}^{-1}$
followed by (9.71), we have
$t=N_{i}^{-1}$
followed by (9.71), we have
 $$\begin{eqnarray}|v_{i}|\leqslant N_{i}^{-1}<\frac{\exp (K^{C_{1}})}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
$$\begin{eqnarray}|v_{i}|\leqslant N_{i}^{-1}<\frac{\exp (K^{C_{1}})}{\unicode[STIX]{x1D70C}_{3}}\end{eqnarray}$$
and hence
 $|\unicode[STIX]{x1D704}(m)\cdot v_{i}|<1$
. The claim follows.
$|\unicode[STIX]{x1D704}(m)\cdot v_{i}|<1$
. The claim follows.
Now we verify (9.63). Let
![]() $a_{0},\unicode[STIX]{x1D709}_{0}$
be as in Proposition 9.16. Let
$a_{0},\unicode[STIX]{x1D709}_{0}$
be as in Proposition 9.16. Let
 $\mathbf{n},\mathbf{n}_{0},\mathbf{h},\mathbf{n}_{1}$
,
$\mathbf{n},\mathbf{n}_{0},\mathbf{h},\mathbf{n}_{1}$
,
![]() $\mathbf{m}_{1}$
be drawn independently and regularly from the Bohr sets
$\mathbf{m}_{1}$
be drawn independently and regularly from the Bohr sets
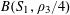 $B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{3}/4)$
,
 $B(S,\unicode[STIX]{x1D70C}_{0})$
,
$B(S,\unicode[STIX]{x1D70C}_{0})$
,
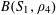 $B(S_{1},\unicode[STIX]{x1D70C}_{4})$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{4})$
,
 $B(S_{1},\unicode[STIX]{x1D70C}_{6})$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{6})$
,
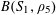 $B(S_{1},\unicode[STIX]{x1D70C}_{5})$
respectively. From Proposition 9.16 we have
$B(S_{1},\unicode[STIX]{x1D70C}_{5})$
respectively. From Proposition 9.16 we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n)|\mathbb{E}f(n_{0}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+\mathbf{h})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}_{0})\mathbf{h})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n)|\mathbb{E}f(n_{0}+\mathbf{h}+a_{0}-n)\overline{f}(n_{0}+\mathbf{h})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}_{0})\mathbf{h})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
Using Lemma 4.4 to replace
![]() $\mathbf{n}$
by
$\mathbf{n}$
by
![]() $\mathbf{n}+\mathbf{n}_{1}$
, and to replace
$\mathbf{n}+\mathbf{n}_{1}$
, and to replace
![]() $\mathbf{h}$
by
$\mathbf{h}$
by
![]() $\mathbf{h}+\mathbf{m}_{1}$
, we have
$\mathbf{h}+\mathbf{m}_{1}$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n,n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n,\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{h}+\mathbf{m}_{1}+a_{0}-n-n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(n_{0}+\mathbf{h}+\mathbf{m}_{1})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}_{0})(\mathbf{h}+\mathbf{m}_{1}))|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n,n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n,\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{h}+\mathbf{m}_{1}+a_{0}-n-n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(n_{0}+\mathbf{h}+\mathbf{m}_{1})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}_{0})(\mathbf{h}+\mathbf{m}_{1}))|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\nonumber\end{eqnarray}$$
and thus by the triangle inequality we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n,n_{1},h}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n,\mathbf{n}_{1}=n_{1},\mathbf{h}=h)|\mathbb{E}f(n_{0}+h+\mathbf{m}_{1}+a_{0}-n-n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(n_{0}+h+\mathbf{m}_{1})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}_{0})(h+\mathbf{m}_{1}))|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n,n_{1},h}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n,\mathbf{n}_{1}=n_{1},\mathbf{h}=h)|\mathbb{E}f(n_{0}+h+\mathbf{m}_{1}+a_{0}-n-n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(n_{0}+h+\mathbf{m}_{1})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}_{0})(h+\mathbf{m}_{1}))|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
The phase
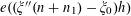 $e((\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}_{0})h)$
is deterministic and may thus be omitted:
$e((\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}_{0})h)$
is deterministic and may thus be omitted:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n,n_{1},h}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n,\mathbf{n}_{1}=n_{1},\mathbf{h}=h)|\mathbb{E}f(n_{0}+h+\mathbf{m}_{1}+a_{0}-n-n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(n_{0}+h+\mathbf{m}_{1})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}_{0})\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n,n_{1},h}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n,\mathbf{n}_{1}=n_{1},\mathbf{h}=h)|\mathbb{E}f(n_{0}+h+\mathbf{m}_{1}+a_{0}-n-n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(n_{0}+h+\mathbf{m}_{1})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}_{0})\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
As the expectation only depends on the sum
![]() $n_{0}+h$
rather than the individual variables
$n_{0}+h$
rather than the individual variables
![]() $n_{0},h$
, we thus have
$n_{0},h$
, we thus have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n,n_{1}}\mathbb{P}(\mathbf{n}_{0}+\mathbf{h}=n_{0},\mathbf{n}=n,\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{0}-n-n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(n_{0}+\mathbf{m}_{1})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}_{0})\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n,n_{1}}\mathbb{P}(\mathbf{n}_{0}+\mathbf{h}=n_{0},\mathbf{n}=n,\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{0}-n-n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(n_{0}+\mathbf{m}_{1})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}_{0})\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
By Lemma 4.4 we may replace
![]() $\mathbf{n}_{0}+\mathbf{h}$
here by
$\mathbf{n}_{0}+\mathbf{h}$
here by
![]() $\mathbf{n}_{0}$
. From (9.57) we have
$\mathbf{n}_{0}$
. From (9.57) we have
 $$\begin{eqnarray}\Vert (\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}^{\prime \prime }(n_{1}))\mathbf{m}_{1}\Vert _{\mathbb{R}/\mathbb{Z}}\ll \unicode[STIX]{x1D702}^{100C_{1}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert (\unicode[STIX]{x1D709}^{\prime \prime }(n+n_{1})-\unicode[STIX]{x1D709}^{\prime \prime }(n)-\unicode[STIX]{x1D709}^{\prime \prime }(n_{1}))\mathbf{m}_{1}\Vert _{\mathbb{R}/\mathbb{Z}}\ll \unicode[STIX]{x1D702}^{100C_{1}}\end{eqnarray}$$
and so
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n,n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n,\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+a_{0}+\mathbf{m}_{1}-n-n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(n_{0}+\mathbf{m}_{1})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)+\unicode[STIX]{x1D709}^{\prime \prime }(n_{1})-\unicode[STIX]{x1D709}_{0})\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n,n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}=n,\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+a_{0}+\mathbf{m}_{1}-n-n_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\overline{f}(n_{0}+\mathbf{m}_{1})e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)+\unicode[STIX]{x1D709}^{\prime \prime }(n_{1})-\unicode[STIX]{x1D709}_{0})\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
By the pigeonhole principle, there thus exists
 $n\in B(S_{\ast },\unicode[STIX]{x1D70C}_{3}/4)$
such that
$n\in B(S_{\ast },\unicode[STIX]{x1D70C}_{3}/4)$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0}\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+a_{0}+\mathbf{m}_{1}-n-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)+\unicode[STIX]{x1D709}^{\prime \prime }(n_{1})-\unicode[STIX]{x1D709}_{0})\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0}\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+a_{0}+\mathbf{m}_{1}-n-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n)+\unicode[STIX]{x1D709}^{\prime \prime }(n_{1})-\unicode[STIX]{x1D709}_{0})\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
which, if we write
 $a_{1}:=a_{0}-n$
and
$a_{1}:=a_{0}-n$
and
 $\unicode[STIX]{x1D709}_{1}:=\unicode[STIX]{x1D709}_{0}-\unicode[STIX]{x1D709}^{\prime \prime }(n)$
, simplifies to
$\unicode[STIX]{x1D709}_{1}:=\unicode[STIX]{x1D709}_{0}-\unicode[STIX]{x1D709}^{\prime \prime }(n)$
, simplifies to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0}\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n_{1})-\unicode[STIX]{x1D709}_{1})\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0}\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e_{p}((\unicode[STIX]{x1D709}^{\prime \prime }(n_{1})-\unicode[STIX]{x1D709}_{1})\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
Since
 $a_{0}\in B(S,3\unicode[STIX]{x1D70C}_{2})$
and
$a_{0}\in B(S,3\unicode[STIX]{x1D70C}_{2})$
and
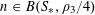 $n\in B(S_{\ast },\unicode[STIX]{x1D70C}_{3}/4)$
, we have
$n\in B(S_{\ast },\unicode[STIX]{x1D70C}_{3}/4)$
, we have
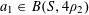 $a_{1}\in B(S,4\unicode[STIX]{x1D70C}_{2})$
.
$a_{1}\in B(S,4\unicode[STIX]{x1D70C}_{2})$
.
Now, from (9.79) one has
 $$\begin{eqnarray}e_{p}(\unicode[STIX]{x1D709}^{\prime \prime }(n_{1})\mathbf{m}_{1})=e(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1}))e(-F(n_{1})\cdot \unicode[STIX]{x1D704}(\mathbf{m}_{1}));\end{eqnarray}$$
$$\begin{eqnarray}e_{p}(\unicode[STIX]{x1D709}^{\prime \prime }(n_{1})\mathbf{m}_{1})=e(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1}))e(-F(n_{1})\cdot \unicode[STIX]{x1D704}(\mathbf{m}_{1}));\end{eqnarray}$$
but since
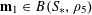 $\mathbf{m}_{1}\in B(S_{\ast },\unicode[STIX]{x1D70C}_{5})$
, we have
$\mathbf{m}_{1}\in B(S_{\ast },\unicode[STIX]{x1D70C}_{5})$
, we have
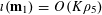 $\unicode[STIX]{x1D704}(\mathbf{m}_{1})=O(K\unicode[STIX]{x1D70C}_{5})$
, and hence by (9.72) we have
$\unicode[STIX]{x1D704}(\mathbf{m}_{1})=O(K\unicode[STIX]{x1D70C}_{5})$
, and hence by (9.72) we have
 $$\begin{eqnarray}\Vert F(n_{1})\cdot \unicode[STIX]{x1D704}(\mathbf{m}_{1})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \unicode[STIX]{x1D702}^{100C_{1}},\end{eqnarray}$$
$$\begin{eqnarray}\Vert F(n_{1})\cdot \unicode[STIX]{x1D704}(\mathbf{m}_{1})\Vert _{\mathbb{R}/\mathbb{Z}}\ll \unicode[STIX]{x1D702}^{100C_{1}},\end{eqnarray}$$
and so
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0};\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0};\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
which gives (9.63). The proof of Theorem 9.18 is now complete.
9.21 Eighth step: making the frequency function symmetric
The next step is the “symmetry step” from [Reference Green and Tao14, Reference Samorodnitsky26], which uses the Cauchy–Schwarz inequality to ensure that
![]() $\unicode[STIX]{x1D6EF}$
is essentially symmetric.
$\unicode[STIX]{x1D6EF}$
is essentially symmetric.
Theorem 9.22. Let the notation and hypotheses be as in Theorem 9.18. For
 $n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{4})$
, define
$n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{4})$
, define
 $$\begin{eqnarray}\{n,m\}:=\unicode[STIX]{x1D6EF}(n,m)-\unicode[STIX]{x1D6EF}(m,n).\end{eqnarray}$$
$$\begin{eqnarray}\{n,m\}:=\unicode[STIX]{x1D6EF}(n,m)-\unicode[STIX]{x1D6EF}(m,n).\end{eqnarray}$$
Then there exists a natural number
![]() $k$
with
$k$
with
 $1\leqslant k\ll \exp (K^{O(C_{1})})$
such that
$1\leqslant k\ll \exp (K^{O(C_{1})})$
such that
 $$\begin{eqnarray}\Vert k\{n,m\}\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant \frac{\Vert n\Vert _{S_{1}^{\bot }}}{\unicode[STIX]{x1D70C}_{8}}\frac{\Vert m\Vert _{S_{1}}}{\unicode[STIX]{x1D70C}_{8}}\end{eqnarray}$$
$$\begin{eqnarray}\Vert k\{n,m\}\Vert _{\mathbb{R}/\mathbb{Z}}\leqslant \frac{\Vert n\Vert _{S_{1}^{\bot }}}{\unicode[STIX]{x1D70C}_{8}}\frac{\Vert m\Vert _{S_{1}}}{\unicode[STIX]{x1D70C}_{8}}\end{eqnarray}$$
for all
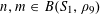 $n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{9})$
.
$n,m\in B(S_{1},\unicode[STIX]{x1D70C}_{9})$
.
Proof. Let
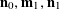 $\mathbf{n}_{0},\mathbf{m}_{1},\mathbf{n}_{1}$
be as in Theorem 9.18. From (9.63) and the pigeonhole principle, we may find
$\mathbf{n}_{0},\mathbf{m}_{1},\mathbf{n}_{1}$
be as in Theorem 9.18. From (9.63) and the pigeonhole principle, we may find
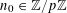 $n_{0}\in \mathbb{Z}/p\mathbb{Z}$
such that
$n_{0}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{1}}\mathbb{P}(\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{1}}\mathbb{P}(\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\nonumber\end{eqnarray}$$
which by the boundedness of the expectation implies
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{1}}\mathbb{P}(\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})|\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{1}}\mathbb{P}(\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})|\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\nonumber\end{eqnarray}$$
and thus we may find a
![]() $1$
-bounded function
$1$
-bounded function
 $b_{1}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
such that
$b_{1}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
such that
 $$\begin{eqnarray}|\mathbb{E}b_{1}(\mathbf{n}_{1})f(n_{0}+\mathbf{m}_{1}+a_{1}-\mathbf{n}_{1})\overline{f}(n_{0}+\mathbf{m}_{1})e(\unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})|\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}b_{1}(\mathbf{n}_{1})f(n_{0}+\mathbf{m}_{1}+a_{1}-\mathbf{n}_{1})\overline{f}(n_{0}+\mathbf{m}_{1})e(\unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})|\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
Writing
 $b_{2}(n):=f(n_{0}+a_{1}+n)$
and
$b_{2}(n):=f(n_{0}+a_{1}+n)$
and
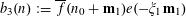 $b_{3}(n):=\overline{f}(n_{0}+\mathbf{m}_{1})e(-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})$
, we may simplify this as
$b_{3}(n):=\overline{f}(n_{0}+\mathbf{m}_{1})e(-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})$
, we may simplify this as
 $$\begin{eqnarray}|\mathbb{E}b_{1}(\mathbf{n}_{1})b_{2}(\mathbf{m}_{1}-\mathbf{n}_{1})b_{3}(\mathbf{m}_{1})e(\unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{m}_{1}))|\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}b_{1}(\mathbf{n}_{1})b_{2}(\mathbf{m}_{1}-\mathbf{n}_{1})b_{3}(\mathbf{m}_{1})e(\unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{m}_{1}))|\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
Using the Cauchy–Schwarz inequality (Lemma 2.1) to eliminate the
![]() $b_{3}(\mathbf{m}_{1})$
factor, we conclude that
$b_{3}(\mathbf{m}_{1})$
factor, we conclude that
 $$\begin{eqnarray}|\mathbb{E}b_{1}(\mathbf{n}_{1})\overline{b_{1}}(\mathbf{n}_{1}^{\prime })b_{2}(\mathbf{m}_{1}-\mathbf{n}_{1})\overline{b_{2}}(\mathbf{m}_{1}-\mathbf{n}_{1}^{\prime })e(\unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D6EF}(\mathbf{n}_{1}^{\prime },\mathbf{m}_{1}))|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)}\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}b_{1}(\mathbf{n}_{1})\overline{b_{1}}(\mathbf{n}_{1}^{\prime })b_{2}(\mathbf{m}_{1}-\mathbf{n}_{1})\overline{b_{2}}(\mathbf{m}_{1}-\mathbf{n}_{1}^{\prime })e(\unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D6EF}(\mathbf{n}_{1}^{\prime },\mathbf{m}_{1}))|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)}\end{eqnarray}$$
where
![]() $\mathbf{n}_{1}^{\prime }$
is an independent copy of
$\mathbf{n}_{1}^{\prime }$
is an independent copy of
![]() $\mathbf{n}_{1}$
. Writing
$\mathbf{n}_{1}$
. Writing
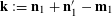 $\mathbf{k}:=\mathbf{n}_{1}+\mathbf{n}_{1}^{\prime }-\mathbf{m}_{1}$
, and noting from the local bilinearity of
$\mathbf{k}:=\mathbf{n}_{1}+\mathbf{n}_{1}^{\prime }-\mathbf{m}_{1}$
, and noting from the local bilinearity of
![]() $\unicode[STIX]{x1D6EF}$
that
$\unicode[STIX]{x1D6EF}$
that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D6EF}(\mathbf{n}_{1}^{\prime },\mathbf{m}_{1}) & = & \displaystyle \unicode[STIX]{x1D6EF}(\mathbf{n}_{1}-\mathbf{n}_{1}^{\prime },\mathbf{m}_{1})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6EF}(\mathbf{n}_{1}-\mathbf{n}_{1}^{\prime },\mathbf{n}_{1}+\mathbf{n}_{1}^{\prime }-\mathbf{k})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{n}_{1})-\unicode[STIX]{x1D6EF}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{1}^{\prime })+\{\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }\}\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{k})+\unicode[STIX]{x1D6EF}(\mathbf{n}_{1}^{\prime },\mathbf{k})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D6EF}(\mathbf{n}_{1}^{\prime },\mathbf{m}_{1}) & = & \displaystyle \unicode[STIX]{x1D6EF}(\mathbf{n}_{1}-\mathbf{n}_{1}^{\prime },\mathbf{m}_{1})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6EF}(\mathbf{n}_{1}-\mathbf{n}_{1}^{\prime },\mathbf{n}_{1}+\mathbf{n}_{1}^{\prime }-\mathbf{k})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{n}_{1})-\unicode[STIX]{x1D6EF}(\mathbf{n}_{1}^{\prime },\mathbf{n}_{1}^{\prime })+\{\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }\}\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D6EF}(\mathbf{n}_{1},\mathbf{k})+\unicode[STIX]{x1D6EF}(\mathbf{n}_{1}^{\prime },\mathbf{k})\nonumber\end{eqnarray}$$
we conclude that
 $$\begin{eqnarray}|\mathbb{E}b_{3}(\mathbf{n}_{1},\mathbf{k})b_{4}(\mathbf{n}_{1}^{\prime },\mathbf{k})e(\{\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)},\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}b_{3}(\mathbf{n}_{1},\mathbf{k})b_{4}(\mathbf{n}_{1}^{\prime },\mathbf{k})e(\{\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)},\end{eqnarray}$$
where
 $b_{3},b_{4}:\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
are the
$b_{3},b_{4}:\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
are the
![]() $1$
-bounded functions
$1$
-bounded functions
 $$\begin{eqnarray}b_{3}(n_{1},k):=b_{1}(n_{1})\overline{b_{2}}(k-n_{1})e(\unicode[STIX]{x1D6EF}(n_{1},n_{1})-\unicode[STIX]{x1D6EF}(n_{1},k))\end{eqnarray}$$
$$\begin{eqnarray}b_{3}(n_{1},k):=b_{1}(n_{1})\overline{b_{2}}(k-n_{1})e(\unicode[STIX]{x1D6EF}(n_{1},n_{1})-\unicode[STIX]{x1D6EF}(n_{1},k))\end{eqnarray}$$
and
 $$\begin{eqnarray}b_{4}(n_{1}^{\prime },k):=\overline{b_{1}}(n_{1}^{\prime })b_{2}(k-n_{1}^{\prime })e(-\unicode[STIX]{x1D6EF}(n_{1}^{\prime },n_{1}^{\prime })+\unicode[STIX]{x1D6EF}(n_{1}^{\prime },k)).\end{eqnarray}$$
$$\begin{eqnarray}b_{4}(n_{1}^{\prime },k):=\overline{b_{1}}(n_{1}^{\prime })b_{2}(k-n_{1}^{\prime })e(-\unicode[STIX]{x1D6EF}(n_{1}^{\prime },n_{1}^{\prime })+\unicode[STIX]{x1D6EF}(n_{1}^{\prime },k)).\end{eqnarray}$$
For fixed
![]() $\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }$
, we see from Lemma 4.4 that
$\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }$
, we see from Lemma 4.4 that
![]() $\mathbf{k}$
differs from
$\mathbf{k}$
differs from
![]() $\mathbf{m}_{1}$
in total variation by
$\mathbf{m}_{1}$
in total variation by
 $O(\unicode[STIX]{x1D702}^{100C_{1}})$
, and hence
$O(\unicode[STIX]{x1D702}^{100C_{1}})$
, and hence
 $$\begin{eqnarray}|\mathbb{E}b_{3}(\mathbf{n}_{1},\mathbf{m}_{1})b_{4}(\mathbf{n}_{1}^{\prime },\mathbf{m}_{1})e(\{\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}b_{3}(\mathbf{n}_{1},\mathbf{m}_{1})b_{4}(\mathbf{n}_{1}^{\prime },\mathbf{m}_{1})e(\{\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)}.\end{eqnarray}$$
By the pigeonhole principle, we may thus find
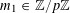 $m_{1}\in \mathbb{Z}/p\mathbb{Z}$
such that
$m_{1}\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}|\mathbb{E}b_{3}(\mathbf{n}_{1},m_{1})b_{4}(\mathbf{n}_{1}^{\prime },m_{1})e(\{\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}b_{3}(\mathbf{n}_{1},m_{1})b_{4}(\mathbf{n}_{1}^{\prime },m_{1})e(\{\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)}.\end{eqnarray}$$
Using Cauchy–Schwarz (Lemma 2.1) to eliminate
 $b_{4}(\mathbf{n}_{1}^{\prime },m_{1})$
, and using the local bilinearity of
$b_{4}(\mathbf{n}_{1}^{\prime },m_{1})$
, and using the local bilinearity of
![]() $\{\,,\}$
, we conclude that
$\{\,,\}$
, we conclude that
 $$\begin{eqnarray}|\mathbb{E}b_{3}(\mathbf{n}_{1},m_{1})\overline{b_{3}}(\mathbf{l}_{1},m_{1})e(\{\mathbf{n}_{1}-\mathbf{l}_{1},\mathbf{n}_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{4C_{1}+O(1)},\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}b_{3}(\mathbf{n}_{1},m_{1})\overline{b_{3}}(\mathbf{l}_{1},m_{1})e(\{\mathbf{n}_{1}-\mathbf{l}_{1},\mathbf{n}_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{4C_{1}+O(1)},\end{eqnarray}$$
where
![]() $\mathbf{l}_{1}$
is an independent copy of
$\mathbf{l}_{1}$
is an independent copy of
![]() $\mathbf{n}_{1}$
; using a further application of Cauchy–Schwarz (Lemma 2.1) to eliminate
$\mathbf{n}_{1}$
; using a further application of Cauchy–Schwarz (Lemma 2.1) to eliminate
 $b_{3}(\mathbf{n}_{1},m_{1})\overline{b_{3}}(\mathbf{l}_{1},m_{1})$
, we conclude that
$b_{3}(\mathbf{n}_{1},m_{1})\overline{b_{3}}(\mathbf{l}_{1},m_{1})$
, we conclude that
 $$\begin{eqnarray}|\mathbb{E}e(\{\mathbf{n}_{1}-\mathbf{l}_{1},\mathbf{n}_{1}^{\prime }-\mathbf{l}_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{8C_{1}+O(1)},\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}e(\{\mathbf{n}_{1}-\mathbf{l}_{1},\mathbf{n}_{1}^{\prime }-\mathbf{l}_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{8C_{1}+O(1)},\end{eqnarray}$$
where
![]() $\mathbf{l}_{1}^{\prime }$
is an independent copy of
$\mathbf{l}_{1}^{\prime }$
is an independent copy of
![]() $\mathbf{n}_{1}^{\prime }$
(thus
$\mathbf{n}_{1}^{\prime }$
(thus
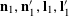 $\mathbf{n}_{1},\mathbf{n}_{1}^{\prime },\mathbf{l}_{1},\mathbf{l}_{1}^{\prime }$
are jointly independent and drawn regularly from
$\mathbf{n}_{1},\mathbf{n}_{1}^{\prime },\mathbf{l}_{1},\mathbf{l}_{1}^{\prime }$
are jointly independent and drawn regularly from
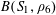 $B(S_{1},\unicode[STIX]{x1D70C}_{6})$
). In particular, by the pigeonhole principle one can find
$B(S_{1},\unicode[STIX]{x1D70C}_{6})$
). In particular, by the pigeonhole principle one can find
 $l_{1},l_{1}^{\prime }\in B(S_{1},\unicode[STIX]{x1D70C}_{6})$
such that
$l_{1},l_{1}^{\prime }\in B(S_{1},\unicode[STIX]{x1D70C}_{6})$
such that
 $$\begin{eqnarray}|\mathbb{E}e(\{\mathbf{n}_{1}-l_{1},\mathbf{n}_{1}^{\prime }-l_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{8C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}e(\{\mathbf{n}_{1}-l_{1},\mathbf{n}_{1}^{\prime }-l_{1}^{\prime }\})|\gg \unicode[STIX]{x1D702}^{8C_{1}+O(1)}.\end{eqnarray}$$
By local bilinearity, one can rewrite
 $\{\mathbf{n}_{1}-l_{1},\mathbf{n}_{1}^{\prime }-l_{1}^{\prime }\}$
as
$\{\mathbf{n}_{1}-l_{1},\mathbf{n}_{1}^{\prime }-l_{1}^{\prime }\}$
as
![]() $\{\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }\}$
plus locally linear functions of
$\{\mathbf{n}_{1},\mathbf{n}_{1}^{\prime }\}$
plus locally linear functions of
![]() $\mathbf{n}_{1}$
and
$\mathbf{n}_{1}$
and
![]() $\mathbf{n}_{1}^{\prime }$
. The claim now follows from Proposition 4.11.◻
$\mathbf{n}_{1}^{\prime }$
. The claim now follows from Proposition 4.11.◻
9.23 Ninth step: integrating the frequency function
We may now finally prove Theorem 8.1. Let the notation and hypotheses be as in that theorem, let
![]() $S_{1}$
and
$S_{1}$
and
![]() $\unicode[STIX]{x1D6EF}$
be as in Theorem 9.18, and let
$\unicode[STIX]{x1D6EF}$
be as in Theorem 9.18, and let
![]() $k$
be as in Theorem 9.22. Thus if we let
$k$
be as in Theorem 9.22. Thus if we let
 $\mathbf{n}_{0},\mathbf{n}_{1},\mathbf{m}_{1}$
be drawn independently and regularly from
$\mathbf{n}_{0},\mathbf{n}_{1},\mathbf{m}_{1}$
be drawn independently and regularly from
 $B(S,\unicode[STIX]{x1D70C}_{0})$
,
$B(S,\unicode[STIX]{x1D70C}_{0})$
,
 $B(S_{1},\unicode[STIX]{x1D70C}_{6})$
,
$B(S_{1},\unicode[STIX]{x1D70C}_{6})$
,
 $B(S_{1},\unicode[STIX]{x1D70C}_{5})$
respectively, we have
$B(S_{1},\unicode[STIX]{x1D70C}_{5})$
respectively, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+m_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{1}=n_{1})|\mathbb{E}f(n_{0}+m_{1}+a_{1}-n_{1})\overline{f}(n_{0}+\mathbf{m}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,e(\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{1})-\unicode[STIX]{x1D709}_{1}\mathbf{m}_{1})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
Now let
![]() $\mathbf{n}_{2},\mathbf{m}_{2}$
be drawn independently and regularly from the Bohr sets
$\mathbf{n}_{2},\mathbf{m}_{2}$
be drawn independently and regularly from the Bohr sets
 $B(S_{1},\unicode[STIX]{x1D70C}_{9}),B(S_{1},\unicode[STIX]{x1D70C}_{10})$
respectively, independently of all previous random variables. By Lemma 4.4, we may replace
$B(S_{1},\unicode[STIX]{x1D70C}_{9}),B(S_{1},\unicode[STIX]{x1D70C}_{10})$
respectively, independently of all previous random variables. By Lemma 4.4, we may replace
![]() $\mathbf{n}_{1},\mathbf{m}_{1}$
by
$\mathbf{n}_{1},\mathbf{m}_{1}$
by
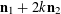 $\mathbf{n}_{1}+2k\mathbf{n}_{2}$
and
$\mathbf{n}_{1}+2k\mathbf{n}_{2}$
and
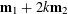 $\mathbf{m}_{1}+2k\mathbf{m}_{2}$
in (9.81), leading to
$\mathbf{m}_{1}+2k\mathbf{m}_{2}$
in (9.81), leading to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\ldots ,\mathbf{n}_{2}=n_{2})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+2k\mathbf{m}_{2}+a_{1}-n_{1}-2kn_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\overline{f}(n_{0}+\mathbf{m}_{1}+2k\mathbf{m}_{2})e(\unicode[STIX]{x1D6EF}(n_{1}+2kn_{2},\mathbf{m}_{1}+2k\mathbf{m}_{2})-\unicode[STIX]{x1D709}_{1}(\mathbf{m}_{1}+2k\mathbf{m}_{2}))|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{1},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\ldots ,\mathbf{n}_{2}=n_{2})|\mathbb{E}f(n_{0}+\mathbf{m}_{1}+2k\mathbf{m}_{2}+a_{1}-n_{1}-2kn_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\overline{f}(n_{0}+\mathbf{m}_{1}+2k\mathbf{m}_{2})e(\unicode[STIX]{x1D6EF}(n_{1}+2kn_{2},\mathbf{m}_{1}+2k\mathbf{m}_{2})-\unicode[STIX]{x1D709}_{1}(\mathbf{m}_{1}+2k\mathbf{m}_{2}))|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\nonumber\end{eqnarray}$$
Thus we may find
 $n_{1}\in B(S_{1},\unicode[STIX]{x1D70C}_{6})$
,
$n_{1}\in B(S_{1},\unicode[STIX]{x1D70C}_{6})$
,
 $m_{1}\in B(S_{1},\unicode[STIX]{x1D70C}_{5})$
such that
$m_{1}\in B(S_{1},\unicode[STIX]{x1D70C}_{5})$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}f(n_{0}+m_{1}+2k\mathbf{m}_{2}+a_{1}-n_{1}-2kn_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\overline{f}(n_{0}+m_{1}+2k\mathbf{m}_{2})e(\unicode[STIX]{x1D6EF}(n_{1}+2kn_{2},m_{1}+2k\mathbf{m}_{2})-\unicode[STIX]{x1D709}_{1}(m_{1}+2k\mathbf{m}_{2}))|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}f(n_{0}+m_{1}+2k\mathbf{m}_{2}+a_{1}-n_{1}-2kn_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\overline{f}(n_{0}+m_{1}+2k\mathbf{m}_{2})e(\unicode[STIX]{x1D6EF}(n_{1}+2kn_{2},m_{1}+2k\mathbf{m}_{2})-\unicode[STIX]{x1D709}_{1}(m_{1}+2k\mathbf{m}_{2}))|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
which we can simplify slightly as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}f(n_{0}+2k\mathbf{m}_{2}+a_{2}-2kn_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\overline{f}(n_{0}+m_{1}+2k\mathbf{m}_{2})e(\unicode[STIX]{x1D6EF}(n_{1}+2kn_{2},m_{1}+2k\mathbf{m}_{2})-2k\unicode[STIX]{x1D709}_{1}\mathbf{m}_{2})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}f(n_{0}+2k\mathbf{m}_{2}+a_{2}-2kn_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\overline{f}(n_{0}+m_{1}+2k\mathbf{m}_{2})e(\unicode[STIX]{x1D6EF}(n_{1}+2kn_{2},m_{1}+2k\mathbf{m}_{2})-2k\unicode[STIX]{x1D709}_{1}\mathbf{m}_{2})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
where
 $a_{2}:=a_{1}+m_{1}-n_{1}$
; since
$a_{2}:=a_{1}+m_{1}-n_{1}$
; since
 $a_{1}\in B(S,4\unicode[STIX]{x1D70C}_{2})$
,
$a_{1}\in B(S,4\unicode[STIX]{x1D70C}_{2})$
,
 $m_{1}\in B(S_{1},\unicode[STIX]{x1D70C}_{5})$
,
$m_{1}\in B(S_{1},\unicode[STIX]{x1D70C}_{5})$
,
 $n_{1}\in B(S_{1},\unicode[STIX]{x1D70C}_{6})$
, we have
$n_{1}\in B(S_{1},\unicode[STIX]{x1D70C}_{6})$
, we have
 $a_{2}\in B(S,5\unicode[STIX]{x1D70C}_{2})$
. By the local bilinearity of
$a_{2}\in B(S,5\unicode[STIX]{x1D70C}_{2})$
. By the local bilinearity of
![]() $\unicode[STIX]{x1D6EF}$
, we have
$\unicode[STIX]{x1D6EF}$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6EF}(n_{1}+2kn_{2},m_{1}+2k\mathbf{m}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6EF}(n_{1},m_{1})+2k\unicode[STIX]{x1D6EF}(n_{2},m_{1})+2k\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{2})+4k^{2}\unicode[STIX]{x1D6EF}(n_{2},\mathbf{m}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6EF}(n_{1},m_{1})+2k\unicode[STIX]{x1D6EF}(n_{2},m_{1})+2k\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{2})+2k^{2}\unicode[STIX]{x1D6EF}(n_{2}+\mathbf{m}_{2},n_{2}+\mathbf{m}_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,2k^{2}\unicode[STIX]{x1D6EF}(n_{2},n_{2})-2k^{2}\unicode[STIX]{x1D6EF}(\mathbf{m}_{2},\mathbf{m}_{2})+2k^{2}\{n_{2},\mathbf{m}_{2}\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6EF}(n_{1}+2kn_{2},m_{1}+2k\mathbf{m}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6EF}(n_{1},m_{1})+2k\unicode[STIX]{x1D6EF}(n_{2},m_{1})+2k\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{2})+4k^{2}\unicode[STIX]{x1D6EF}(n_{2},\mathbf{m}_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6EF}(n_{1},m_{1})+2k\unicode[STIX]{x1D6EF}(n_{2},m_{1})+2k\unicode[STIX]{x1D6EF}(n_{1},\mathbf{m}_{2})+2k^{2}\unicode[STIX]{x1D6EF}(n_{2}+\mathbf{m}_{2},n_{2}+\mathbf{m}_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,2k^{2}\unicode[STIX]{x1D6EF}(n_{2},n_{2})-2k^{2}\unicode[STIX]{x1D6EF}(\mathbf{m}_{2},\mathbf{m}_{2})+2k^{2}\{n_{2},\mathbf{m}_{2}\}\nonumber\end{eqnarray}$$
and so we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}F(n_{0},n_{2}-\mathbf{m}_{2})G(n_{0},\mathbf{m}_{2})e(2k^{2}\{n_{2},\mathbf{m}_{2}\})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}F(n_{0},n_{2}-\mathbf{m}_{2})G(n_{0},\mathbf{m}_{2})e(2k^{2}\{n_{2},\mathbf{m}_{2}\})|^{2}\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{C_{1}+O(1)},\nonumber\end{eqnarray}$$
where
 $$\begin{eqnarray}F(n,m):=f(n+a_{2}-2km)e(-k^{2}\unicode[STIX]{x1D6EF}(m,m))\end{eqnarray}$$
$$\begin{eqnarray}F(n,m):=f(n+a_{2}-2km)e(-k^{2}\unicode[STIX]{x1D6EF}(m,m))\end{eqnarray}$$
and
 $$\begin{eqnarray}G(n,m):=\overline{f}(n+m_{1}+2km)e(2k\unicode[STIX]{x1D6EF}(n_{1},m)-2k^{2}\unicode[STIX]{x1D6EF}(m,m)-2k\unicode[STIX]{x1D709}_{1}m).\end{eqnarray}$$
$$\begin{eqnarray}G(n,m):=\overline{f}(n+m_{1}+2km)e(2k\unicode[STIX]{x1D6EF}(n_{1},m)-2k^{2}\unicode[STIX]{x1D6EF}(m,m)-2k\unicode[STIX]{x1D709}_{1}m).\end{eqnarray}$$
By Theorem 9.22, one has
 $\Vert k\{\mathbf{n}_{2},\mathbf{m}_{2}\}\Vert _{\mathbb{R}/\mathbb{Z}}\ll \unicode[STIX]{x1D702}^{100C_{1}}$
, and thus
$\Vert k\{\mathbf{n}_{2},\mathbf{m}_{2}\}\Vert _{\mathbb{R}/\mathbb{Z}}\ll \unicode[STIX]{x1D702}^{100C_{1}}$
, and thus
 $$\begin{eqnarray}\mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}F(n_{0},n_{2}-\mathbf{m}_{2})G(n_{0},\mathbf{m}_{2})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}F(n_{0},n_{2}-\mathbf{m}_{2})G(n_{0},\mathbf{m}_{2})|^{2}\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}.\end{eqnarray}$$
By boundedness of the expectation, this implies that
 $$\begin{eqnarray}\mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}F(n_{0},n_{2}-\mathbf{m}_{2})G(n_{0},\mathbf{m}_{2})|\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}F(n_{0},n_{2}-\mathbf{m}_{2})G(n_{0},\mathbf{m}_{2})|\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\end{eqnarray}$$
and thus
 $$\begin{eqnarray}|\mathbb{E}F(\mathbf{n}_{0},\mathbf{n}_{2}-\mathbf{m}_{2})G(\mathbf{n}_{0},\mathbf{m}_{2})H(\mathbf{n}_{0},\mathbf{n}_{2})|\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}F(\mathbf{n}_{0},\mathbf{n}_{2}-\mathbf{m}_{2})G(\mathbf{n}_{0},\mathbf{m}_{2})H(\mathbf{n}_{0},\mathbf{n}_{2})|\gg \unicode[STIX]{x1D702}^{C_{1}+O(1)}\end{eqnarray}$$
for some
![]() $1$
-bounded function
$1$
-bounded function
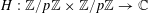 $H:\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
. By Cauchy–Schwarz (Lemma 2.1), we thus have
$H:\mathbb{Z}/p\mathbb{Z}\times \mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}$
. By Cauchy–Schwarz (Lemma 2.1), we thus have
 $$\begin{eqnarray}|\mathbb{E}F(\mathbf{n}_{0},\mathbf{n}_{2}-\mathbf{m}_{2})G(\mathbf{n}_{0},\mathbf{m}_{2})\overline{F}(\mathbf{n}_{0},\mathbf{n}_{2}-\mathbf{m}_{2}^{\prime })\overline{G}(\mathbf{n}_{0},\mathbf{m}_{2})|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)},\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}F(\mathbf{n}_{0},\mathbf{n}_{2}-\mathbf{m}_{2})G(\mathbf{n}_{0},\mathbf{m}_{2})\overline{F}(\mathbf{n}_{0},\mathbf{n}_{2}-\mathbf{m}_{2}^{\prime })\overline{G}(\mathbf{n}_{0},\mathbf{m}_{2})|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)},\end{eqnarray}$$
where
![]() $\mathbf{m}_{2}^{\prime }$
is an independent copy of
$\mathbf{m}_{2}^{\prime }$
is an independent copy of
![]() $\mathbf{m}_{2}$
; by a second application of Cauchy–Schwarz (Lemma 2.1), we then have
$\mathbf{m}_{2}$
; by a second application of Cauchy–Schwarz (Lemma 2.1), we then have
 $$\begin{eqnarray}|\mathbb{E}F(\mathbf{n}_{0},\mathbf{n}_{2}-\mathbf{m}_{2})\overline{F}(\mathbf{n}_{0},\mathbf{n}_{2}-\mathbf{m}_{2}^{\prime })\overline{F}(\mathbf{n}_{0},\mathbf{n}_{2}^{\prime }-\mathbf{m}_{2})F(\mathbf{n}_{0},\mathbf{n}_{2}^{\prime }-\mathbf{m}_{2}^{\prime })|\gg \unicode[STIX]{x1D702}^{4C_{1}+O(1)},\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}F(\mathbf{n}_{0},\mathbf{n}_{2}-\mathbf{m}_{2})\overline{F}(\mathbf{n}_{0},\mathbf{n}_{2}-\mathbf{m}_{2}^{\prime })\overline{F}(\mathbf{n}_{0},\mathbf{n}_{2}^{\prime }-\mathbf{m}_{2})F(\mathbf{n}_{0},\mathbf{n}_{2}^{\prime }-\mathbf{m}_{2}^{\prime })|\gg \unicode[STIX]{x1D702}^{4C_{1}+O(1)},\end{eqnarray}$$
where
![]() $\mathbf{n}_{2}^{\prime }$
is an independent copy of
$\mathbf{n}_{2}^{\prime }$
is an independent copy of
![]() $\mathbf{n}_{2}$
. Since the distributions of
$\mathbf{n}_{2}$
. Since the distributions of
![]() $\mathbf{m}_{2},\mathbf{m}_{2}^{\prime }$
are symmetric, we thus have
$\mathbf{m}_{2},\mathbf{m}_{2}^{\prime }$
are symmetric, we thus have
 $$\begin{eqnarray}|\mathbb{E}F(\mathbf{n}_{0},\mathbf{n}_{2}+\mathbf{m}_{2})\overline{F}(\mathbf{n}_{0},\mathbf{n}_{2}+\mathbf{m}_{2}^{\prime })\overline{F}(\mathbf{n}_{0},\mathbf{n}_{2}^{\prime }+\mathbf{m}_{2})F(\mathbf{n}_{0},\mathbf{n}_{2}^{\prime }+\mathbf{m}_{2}^{\prime })|\gg \unicode[STIX]{x1D702}^{4C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}F(\mathbf{n}_{0},\mathbf{n}_{2}+\mathbf{m}_{2})\overline{F}(\mathbf{n}_{0},\mathbf{n}_{2}+\mathbf{m}_{2}^{\prime })\overline{F}(\mathbf{n}_{0},\mathbf{n}_{2}^{\prime }+\mathbf{m}_{2})F(\mathbf{n}_{0},\mathbf{n}_{2}^{\prime }+\mathbf{m}_{2}^{\prime })|\gg \unicode[STIX]{x1D702}^{4C_{1}+O(1)}.\end{eqnarray}$$
In particular, with probability
 $\gg \unicode[STIX]{x1D702}^{4C_{1}+O(1)}$
, the random variable
$\gg \unicode[STIX]{x1D702}^{4C_{1}+O(1)}$
, the random variable
![]() $\mathbf{n}_{0}$
attains a value
$\mathbf{n}_{0}$
attains a value
![]() $n_{0}$
for which
$n_{0}$
for which
 $$\begin{eqnarray}|\mathbb{E}F(n_{0},\mathbf{n}_{2}+\mathbf{m}_{2})\overline{F}(n_{0},\mathbf{n}_{2}+\mathbf{m}_{2}^{\prime })\overline{F}(n_{0},\mathbf{n}_{2}^{\prime }+\mathbf{m}_{2})F(n_{0},\mathbf{n}_{2}^{\prime }+\mathbf{m}_{2}^{\prime })|\gg \unicode[STIX]{x1D702}^{4C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}|\mathbb{E}F(n_{0},\mathbf{n}_{2}+\mathbf{m}_{2})\overline{F}(n_{0},\mathbf{n}_{2}+\mathbf{m}_{2}^{\prime })\overline{F}(n_{0},\mathbf{n}_{2}^{\prime }+\mathbf{m}_{2})F(n_{0},\mathbf{n}_{2}^{\prime }+\mathbf{m}_{2}^{\prime })|\gg \unicode[STIX]{x1D702}^{4C_{1}+O(1)}.\end{eqnarray}$$
If
![]() $n_{0}$
is such that (9.83) holds, then we may apply Theorem 4.12 and conclude that there exists a frequency
$n_{0}$
is such that (9.83) holds, then we may apply Theorem 4.12 and conclude that there exists a frequency
 $\unicode[STIX]{x1D6FD}(n_{0})\in \mathbb{Z}/p\mathbb{Z}$
such that
$\unicode[STIX]{x1D6FD}(n_{0})\in \mathbb{Z}/p\mathbb{Z}$
such that
 $$\begin{eqnarray}\biggl|\mathop{\sum }_{n_{2}}\mathbb{P}(\mathbf{n}_{2}=n_{2})\mathbb{E}F(n_{0},n_{2}+\mathbf{m}_{2})e(-\unicode[STIX]{x1D6FD}(n_{0})\mathbf{m}_{2})\biggr|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)}\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\mathop{\sum }_{n_{2}}\mathbb{P}(\mathbf{n}_{2}=n_{2})\mathbb{E}F(n_{0},n_{2}+\mathbf{m}_{2})e(-\unicode[STIX]{x1D6FD}(n_{0})\mathbf{m}_{2})\biggr|\gg \unicode[STIX]{x1D702}^{2C_{1}+O(1)}\end{eqnarray}$$
and thus (defining
![]() $\unicode[STIX]{x1D6FD}(n_{0})$
arbitrarily if (9.83) does not hold),
$\unicode[STIX]{x1D6FD}(n_{0})$
arbitrarily if (9.83) does not hold),
 $$\begin{eqnarray}\mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}F(n_{0},n_{2}+\mathbf{m}_{2})e(-\unicode[STIX]{x1D6FD}(n_{0})\mathbf{m}_{2})|\gg \unicode[STIX]{x1D702}^{6C_{1}+O(1)}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0},n_{2}}\mathbb{P}(\mathbf{n}_{0}=n_{0},\mathbf{n}_{2}=n_{2})|\mathbb{E}F(n_{0},n_{2}+\mathbf{m}_{2})e(-\unicode[STIX]{x1D6FD}(n_{0})\mathbf{m}_{2})|\gg \unicode[STIX]{x1D702}^{6C_{1}+O(1)}\end{eqnarray}$$
and hence there exists
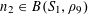 $n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{9})$
with
$n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{9})$
with
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}F(n_{0},n_{2}+\mathbf{m}_{2})e(-\unicode[STIX]{x1D6FD}(n_{0})\mathbf{m}_{2})|\gg \unicode[STIX]{x1D702}^{6C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}F(n_{0},n_{2}+\mathbf{m}_{2})e(-\unicode[STIX]{x1D6FD}(n_{0})\mathbf{m}_{2})|\gg \unicode[STIX]{x1D702}^{6C_{1}+O(1)}.\end{eqnarray}$$
Applying (9.82), we conclude that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+a_{3}-2k\mathbf{m}_{2})e(-k^{2}\unicode[STIX]{x1D6EF}(\mathbf{m}_{2},\mathbf{m}_{2})-\unicode[STIX]{x1D6FD}(n_{0})\mathbf{m}_{2})|\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{6C_{1}+O(1)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}+a_{3}-2k\mathbf{m}_{2})e(-k^{2}\unicode[STIX]{x1D6EF}(\mathbf{m}_{2},\mathbf{m}_{2})-\unicode[STIX]{x1D6FD}(n_{0})\mathbf{m}_{2})|\nonumber\\ \displaystyle & & \displaystyle \quad \gg \unicode[STIX]{x1D702}^{6C_{1}+O(1)},\nonumber\end{eqnarray}$$
where
 $a_{3}:=a_{2}-2kn_{2}$
; since
$a_{3}:=a_{2}-2kn_{2}$
; since
 $a_{2}\in B(S,5\unicode[STIX]{x1D70C}_{2})$
,
$a_{2}\in B(S,5\unicode[STIX]{x1D70C}_{2})$
,
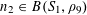 $n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{9})$
, and
$n_{2}\in B(S_{1},\unicode[STIX]{x1D70C}_{9})$
, and
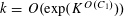 $k=O(\exp (K^{O(C_{1})}))$
, we have
$k=O(\exp (K^{O(C_{1})}))$
, we have
 $a_{3}\in B(S,6\unicode[STIX]{x1D70C}_{2})$
. In particular, by Lemma 4.4,
$a_{3}\in B(S,6\unicode[STIX]{x1D70C}_{2})$
. In particular, by Lemma 4.4,
![]() $\mathbf{n}_{0}$
and
$\mathbf{n}_{0}$
and
![]() $\mathbf{n}_{0}+a_{3}$
differ in total variation by
$\mathbf{n}_{0}+a_{3}$
differ in total variation by
 $O(\unicode[STIX]{x1D702}^{100C_{1}+O(1)})$
, and thus
$O(\unicode[STIX]{x1D702}^{100C_{1}+O(1)})$
, and thus
 $$\begin{eqnarray}\mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}-2k\mathbf{m}_{2})e(-k^{2}\unicode[STIX]{x1D6EF}(\mathbf{m}_{2},\mathbf{m}_{2})-\unicode[STIX]{x1D6FD}(n_{0})\mathbf{m}_{2})|\gg \unicode[STIX]{x1D702}^{6C_{1}+O(1)}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n_{0}}\mathbb{P}(\mathbf{n}_{0}=n_{0})|\mathbb{E}f(n_{0}-2k\mathbf{m}_{2})e(-k^{2}\unicode[STIX]{x1D6EF}(\mathbf{m}_{2},\mathbf{m}_{2})-\unicode[STIX]{x1D6FD}(n_{0})\mathbf{m}_{2})|\gg \unicode[STIX]{x1D702}^{6C_{1}+O(1)}.\end{eqnarray}$$
Theorem 8.1 then follows after a change of variables, noting that the map
 $\mathbf{m}_{2}\mapsto \unicode[STIX]{x1D6EF}(\mathbf{m}_{2},\mathbf{m}_{2})$
is locally quadratic on
$\mathbf{m}_{2}\mapsto \unicode[STIX]{x1D6EF}(\mathbf{m}_{2},\mathbf{m}_{2})$
is locally quadratic on
 $B(S_{1},\unicode[STIX]{x1D70C}_{9})$
.
$B(S_{1},\unicode[STIX]{x1D70C}_{9})$
.
Acknowledgements
The first author is supported by a Simons Investigator grant. The second author is supported by a Simons Investigator grant, the James and Carol Collins Chair, the Mathematical Analysis & Application Research Fund Endowment, and by NSF grant DMS-1266164. Part of this paper was written while the authors were in residence at MSRI in spring 2017, which is supported by NSF grant DMS-1440140.
We are indebted to the anonymous referee for helpful corrections and suggestions. Finally, we thank any readers interested in the result of this paper for their patience. Most of the argument was worked out by us in 2005, and the result was claimed in [Reference Green, Tao, Chen, Gowers, Halberstam, Schmidt and Vaughan19], dedicated to Roth’s 80th birthday. While a complete, though not very readable, version has been available on request since around 2012, it has taken us until now to create a potentially publishable manuscript.