Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Finkel, Olivier
and
Todorčević, Stevo
2012.
A hierarchy of tree-automatic structures.
The Journal of Symbolic Logic,
Vol. 77,
Issue. 1,
p.
350.
Farah, Ilijas
and
Shelah, Saharon
2014.
Trivial automorphisms.
Israel Journal of Mathematics,
Vol. 201,
Issue. 2,
p.
701.
Farah, Ilijas
2017.
Logic Colloquium 2000.
p.
252.
Farah, Ilijas
2019.
Combinatorial Set Theory of C*-algebras.
p.
241.
FARAH, ILIJAS
GHASEMI, SAEED
VACCARO, ANDREA
and
VIGNATI, ALESSANDRO
2025.
CORONA RIGIDITY.
The Bulletin of Symbolic Logic,
Vol. 31,
Issue. 2,
p.
195.

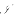 on
on 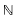 satisfy the following requirement: any measurable homomorphism
satisfy the following requirement: any measurable homomorphism 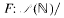
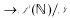 has a continuous lifting
has a continuous lifting 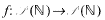 which is a homomorphism itself. Ideals having such a property were called
which is a homomorphism itself. Ideals having such a property were called 