Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-30T19:24:05.804Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-σ-finite sets for packing measure

Part of: Classical measure theory

Published online by Cambridge University Press:  26 February 2010

H. Haase
H. Haase
Affiliation:
Sektion Mathematik, Ernst-Moritz-Arndt Universität, DDR-2200 Greifswald, F.-L. Jahn Str. 15a.
Get access

Extract

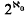In a recent paper Taylor and Tricot [10] introduced packing measures in ℝd. We modify their definition slightly to extend it to a general metric space. Our main concern is to show that in any complete separable metric space every analytic set of non-σ-finite h-packing measure contains disjoint compact subsets each of non-σ-finite measure. The corresponding problem for Hausdorff measures is discussed, but not completely resolved, in Rogers' book [7]. We also show that packing measure cannot be attained by taking the Hausdorff measure with respect to a different increasing function using another metric which generates the same topology. This means that the class of pacing measures is distinct from the class of Hausdorff measures.

MSC classification

Secondary: 28A12: Contents, measures, outer measures, capacities
Type
Research Article
Information
Mathematika , Volume 33 , Issue 1 , June 1986 , pp. 129 - 136
Copyright
Copyright © University College London 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Davies, Roy O.. A Theorem on the existence of non-σ-finite subsets. Mathematika, 15 (1968), 60–62.CrossRefGoogle Scholar
2.Davies, Roy O.. Increasing sequences of sets and Hausdorff measure. Proc. London Math. Soc. (3), 20 (1970), 222–236.CrossRefGoogle Scholar
3.Engelking, R.. General Topology (PWN, Warszawa, 1977).Google Scholar
4.Hausdorff, F.. Erweiterung einer Homöomorphie. Fund. Math., 16 (1930), 353–360.Google Scholar
5.Larman, D. G.. On the selection of compact subsets of positive measure from analytic sets of positive measure. Can. J. Math., 26 (3), (1974), 665–677.CrossRefGoogle Scholar
6.Larman, D. G.. On the selection of non-σ-finite subsets. Mathematika, 14 (1967), 161–164.Google Scholar
7.Rogers, C. A.. Hausdorff measures (Cambridge University Press, 1970).Google Scholar
8.Sion, M. and Sjerve, D.. Approximation properties of measures generated by continuous set functions. Mathematika, 9 (1962), 145–156.CrossRefGoogle Scholar
9.Tricot, C.. Two definitions of fractional dimension. Math. Proc. Camb. Phil. Soc., 91 (1982), 57–74.Google Scholar
10.Taylor, S. J. and Tricot, C.. Packing measure and its evaluation for a Brownian path. Tran. Amer. Math. Soc., 288 (1985), 679–699.CrossRefGoogle Scholar