Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bourgain, J.
1991.
On the Busemann-Petty problem for perturbations of the ball.
Geometric and Functional Analysis,
Vol. 1,
Issue. 1,
p.
1.
Papadimitrakis, Michael
1992.
On the Busemann‐Petty problem about convex, centrally symmetric bodies in.
Mathematika,
Vol. 39,
Issue. 2,
p.
258.
LUTWAK, Erwin
1993.
Handbook of Convex Geometry.
p.
151.
Gardner, R. J.
1994.
Intersection bodies and the Busemann-Petty problem.
Transactions of the American Mathematical Society,
Vol. 342,
Issue. 1,
p.
435.
Koldobsky, Alexander
1997.
Intersection bodies and the Busemann-Petty problem.
Comptes Rendus de l'Académie des Sciences - Series I - Mathematics,
Vol. 325,
Issue. 11,
p.
1181.
Koldobsky, Alexander
1998.
Second Derivative Test for Intersection Bodies.
Advances in Mathematics,
Vol. 136,
Issue. 1,
p.
15.
Koldobsky, Alexander
1998.
Intersection Bodies in R4.
Advances in Mathematics,
Vol. 136,
Issue. 1,
p.
1.
Koldobsky, A.
1999.
A generalization of the Busemann-Petty problem on sections of convex bodies.
Israel Journal of Mathematics,
Vol. 110,
Issue. 1,
p.
75.
Gardner, Richard J.
Koldobsky, Alexander
and
Schlumprecht, Thomas
1999.
An analytic solution to the Busemann-Petty problem.
Comptes Rendus de l'Académie des Sciences - Series I - Mathematics,
Vol. 328,
Issue. 1,
p.
29.
Barthe, F.
Fradelizi, M.
and
Maurey, B.
1999.
A Short Solution to the Busemann-Petty Problem.
Positivity,
Vol. 3,
Issue. 1,
p.
95.
Campi, Stefano
1999.
Convex intersection bodies in three and four dimensions.
Mathematika,
Vol. 46,
Issue. 1,
p.
15.
2001.
Vol. 1,
Issue. ,
p.
161.
2001.
Vol. 1,
Issue. ,
p.
899.
Barthe, Franck
2003.
Autour de l'inégalité de Brunn-Minkowski.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 12,
Issue. 2,
p.
127.
Koldobsky, Alexander
2003.
The Busemann–Petty problem via spherical harmonics.
Advances in Mathematics,
Vol. 177,
Issue. 1,
p.
105.
Zvavitch, A.
2004.
Gaussian measure of sections of convex bodies.
Advances in Mathematics,
Vol. 188,
Issue. 1,
p.
124.
Rubin, Boris
and
Zhang, Gaoyong
2004.
Generalizations of the Busemann–Petty problem for sections of convex bodies.
Journal of Functional Analysis,
Vol. 213,
Issue. 2,
p.
473.
Koldobsky, A.
Ryabogin, D.
and
Zvavitch, Artem
2004.
Fourier Analysis and Convexity.
p.
119.
Milman, Emanuel
2006.
Generalized intersection bodies.
Journal of Functional Analysis,
Vol. 240,
Issue. 2,
p.
530.
Lü, Song-jun
and
Leng, Gang-song
2007.
On the generalized Busemann-Petty problem.
Science in China Series A: Mathematics,
Vol. 50,
Issue. 8,
p.
1103.

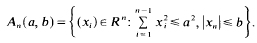
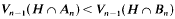 for every (
for every (