Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-30T19:33:45.585Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on involutary division algebras of the second kind

Part of: Ring extensions and related topics

Published online by Cambridge University Press:  26 February 2010

C. J. Bushnell
C. J. Bushnell
Affiliation:
University of London King's College, Strand, London WC2R 2LS.
Get access

Extract

Let L/K be a quadratic extension of algebraic number fields, and D a central L-division algebra of finite L-dimension d2. If - is an involution (i.e., a ring antiautomorphism of period two) of D, we write S(-) for the set of - symmetric elements of D:

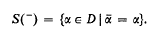
MSC classification

Secondary: 13B10: Morphisms
Type
Research Article
Information
Mathematika , Volume 24 , Issue 1 , June 1977 , pp. 34 - 36
Copyright
Copyright © University College London 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Albert, A. A.. Structure of.Algebras (A.M.S. Colloquium Publications XXIV, Providence R.I., 1961).Google Scholar
2.Artin, E. and Tate, J. T.. Class Field Theory (Benjamin, New York, 1967).Google Scholar
3.Cassels, J. W. S. and Fröhlich, A.. Algebraic Number Theory (Academic Press, London, 1967).Google Scholar
4.Fröhlich, A.. “Symplectic local constants and Hermitian Galois module structure”. (Proceedings of an International Symposium on algebraic number theory, Kyoto, 1976. To appear.)Google Scholar
5.Kneser, M.. Lectures on the Galois cohomology of the classical groups. (Tata Institute of Fundamental Research, Bombay, 1969).Google Scholar
6.Weil, A.. Basic Number Theory (Springer-Verlag, Berlin, 1968).Google Scholar