Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Galovich, S.
Reiner, I.
and
Ullom, S.
1972.
Class groups for integral representations of metacyclic groups.
Mathematika,
Vol. 19,
Issue. 1,
p.
105.
Reiner, I.
and
Ullom, S.
1973.
Proceedings of the Conference on Orders, Group Rings and Related Topics.
Vol. 353,
Issue. ,
p.
139.
Reiner, I
and
Ullom, S
1974.
A Mayer-Vietoris sequence for class groups.
Journal of Algebra,
Vol. 31,
Issue. 2,
p.
305.
Reiner, Irving
1975.
Representations of Algebras.
Vol. 488,
Issue. ,
p.
253.
Cassou-Noguès, Philippe
1976.
Groupe des classes de l'algèbre d'un groupe métacyclique.
Journal of Algebra,
Vol. 41,
Issue. 1,
p.
116.
Kervaire, Michel A.
and
Murthy, M. Pavaman
1977.
On the projective class group of cyclic groups of prime power order.
Commentarii Mathematici Helvetici,
Vol. 52,
Issue. 1,
p.
415.
Oliver, Robert
1985.
Orders and their Applications.
Vol. 1142,
Issue. ,
p.
211.

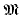 ), Γ a finite abelian group,
), Γ a finite abelian group, 