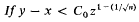Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Baker, A.
1978.
Transcendence theory and its applications.
Journal of the Australian Mathematical Society,
Vol. 25,
Issue. 4,
p.
438.
Ribenboim, Paulo
1979.
13 Lectures on Fermat’s Last Theorem.
p.
225.
Turk, Jan
1983.
A note on the Fermat equation.
Journal of Number Theory,
Vol. 17,
Issue. 1,
p.
76.
Brindza, B.
Gy�ry, K.
and
Tijdeman, R.
1985.
The Fermat equation with polynomial values as base variables.
Inventiones Mathematicae,
Vol. 80,
Issue. 1,
p.
139.
1999.
Fermat’s Last Theorem for Amateurs.
p.
99.
Bennett, Michael A.
and
Das, Pranabesh
2025.
Gaps between cubes with perfect power sum.
Bulletin of the London Mathematical Society,
Vol. 57,
Issue. 10,
p.
3051.