Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schneider, Rolf
1979.
Contributions to Geometry.
p.
13.
Bauer, Christina
1996.
Minimal and reduced pairs of convex bodies.
Geometriae Dedicata,
Vol. 62,
Issue. 2,
p.
179.

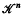 denote the set of all convex bodies in
denote the set of all convex bodies in