No CrossRef data available.
Article contents
On capitulation in certain Zl-extensions of number fields
Published online by Cambridge University Press: 26 February 2010
Extract
Let F be a number field, l a prime, and K a normal extension of F for which Gal(K/F) is topologically isomorphic to the additive group Zl. Then, corresponding to the subgroups ln Zl, there is a chain of fields F = F0 ⊂ F1 ⊂ F2 ⊂ … ⊂ K so that Gal (Fn/F) is cyclic of order ln. Let An be the l-Sylow subgroup of the ideal class group of Fn. By the now well-known theorem of Iwasawa, there are constants μ, λ and ν so that, for all sufficiently large n, |An| = len, where en = μln + λn + ν. Much work has been done investigating these constants, especially showing μ to be 0 for cyclotomic Zl-extensions of abelian fields F, [2], and computing λ and ν in special cases. In many cases, it has been shown that μ = λ = 0, and I know of no cases where μ or λ are positive when F is totally real (cf. Greenberg [3]). Here we investigate the maps in,m: An → Am induced by the inclusion of Fn in Fm for m ≥ n, with a view to determining their kernels. When μ = λ = 0, we prove that in, n+s(An) = 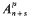 for large enough n, and that, for large enough n, Ker in, n+s coincides with the kernel of the ls power map on An. I thank A. Brumer for helpful conversations on this matter.
for large enough n, and that, for large enough n, Ker in, n+s coincides with the kernel of the ls power map on An. I thank A. Brumer for helpful conversations on this matter.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1983

