Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T06:28:27.621Z Has data issue: false hasContentIssue false
  • English
  • Français

On l-class groups of certain number fields

Published online by Cambridge University Press:  26 February 2010

Frank Gerth III
Frank Gerth III
Affiliation:
Department of Mathematics, University of Texas, Austin, Texas 78712, U. S. A.
Get access

Extract

Let M be a finite extension field of the rational numbers Q, and let CM denote the ideal class group of M. Let l be a rational prime, and let AM denote the l-class group of M (i.e., the Sylow l-subgroup of CM). If G is any finite abelian l-group, we define

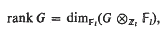
where ℤl is the ring of l-adic integers and Fl is the finite field of l elements. One of the classical results of algebraic number theory is the specification of rank AM when M is a quadratic extension of Q and l = 2. This result was obtained by means of Gauss's theory of genera. A generalization of this result can be found in [1], where A. Fröhlich has obtained upper and lower bounds for rank AM when M is a cyclic extension of Q of degree l. His methods also show how to compute rank AM exactly when l = 3. In [4], G. Gras has described a procedure for analyzing the l-class groups of relatively cyclic extensions of degree l. However when l > 3, the computations can be very difficult.

Type
Research Article
Information
Mathematika , Volume 23 , Issue 1 , June 1976 , pp. 116 - 123
Copyright
Copyright © University College London 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Fröhlich, A.. “The generalization of a theorem of L. Redei's,” Quart. J. Math. Oxford, (2), 5 (1954), 130–140.CrossRefGoogle Scholar
2.Gerth, F.. “On 3-class groups of pure cubic fields,” J. Reine Angew. Math., 278/279 (1975), 52–62.Google Scholar
3.Gerth, F.. “Ranks of 3-class groups of non-Galois cubic fields,” to appear in Acta Arithmetica.Google Scholar
4.Gras, G.. Sur les l-classes d'idéaux dans les extensions cycliques relatives de degré permier I, Thesis (Grenoble, 1972).CrossRefGoogle Scholar
5.Gras, G.. “Sur les l-classes d'ideaux des extensions non galoisiennes de Q de degré premier impair l a clôture galoisiennes diédrale de degré 2l,” J. Math. Soc. Japan, 26 (1974), 677–685.Google Scholar
6.Hasse, H.. “Bericht über neuere Untersuchungen und Probleme aus der Theorie der algebraischen Zahlkörper, la,” Jber. Deutsch. Math.-Verein., 36 (1927), 233–311.Google Scholar
7.Iwasawa, K.. “A note on the group of units of an algebraic number field,” J. Math. Pures Appi, ser. 9, 35 (1956), 189–192.Google Scholar
8.Kobayashi, S.. “On the l-class rank in some algebraic number fields,” J. Math. Soc. Japan, 26 (1974), 668–676.CrossRefGoogle Scholar
9.Lang, S.. Algebraic number theory (Addison-Wesley, Reading, Mass., 1970).Google Scholar