Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-15T13:36:52.457Z Has data issue: false hasContentIssue false
  • English
  • Français

On sigma-phi numbers

Published online by Cambridge University Press:  26 February 2010

Robert C. Vaughan  and
Kevin L. Weis
Robert C. Vaughan
Affiliation:
Department of Mathematics, McAllister Building, Pennsylvania State University, University Park, PA 16802-6401, U.S.A. E-mail: rvaughan@math.psu.edu.
Kevin L. Weis
Affiliation:
Department of Mathematics, The College of New Jersey, Holman Hall 231, PO Box 7718, 2000 Pennington Road, Ewing, NJ 08628-0718, U.S.A.Current address: Mathematics Department, UCLA, Box 951555, Los Angeles, CA 90095-1555, U.S.A. E-mail: kweis@math.ucla.edu
Get access

Extract

Let

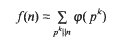
where φ denotes Euler's function. In this memoir we study the set w of sigmaphi numbers, that is, those composite natural numbers n which satisfy

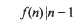
The smallest such number is 65, and they appear to be moderately frequent. There are 290 sigma-phi numbers not exceeding 105 and 1,231 not exceeding 106. By comparison, we observe that the number of primes in these ranges is 9,592 and 78,498, respectively. Since the primes also satisfy the relationship (1.2) a sigma-phi number can be thought of as a kind of pseudo-prime. The motivation for studying sigma-phi numbers is that they should have similar properties to Carmichael numbers but be easier to study. A Carmichael number is a number n such that the least common multiple of the φ(pk) with pk||n divides n-1, i.e., by Korseldt's criterion, a number for which p-1||n-1 whenever p|n. The number of Carmichael numbers not exceeding 105 and 106 is 16 and 43, respectively. It seems that the counting functions for Carmichael and sigma-phi numbers have somewhat similar growth rates. The counts above are skewed by the fact that there are many sigma-phi numbers with exactly two prime factors but there are no Carmichael numbers of this kind.

Type
Research Article
Information
Mathematika , Volume 48 , Issue 1-2 , December 2001 , pp. 169 - 189
Copyright
Copyright © University College London 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Alford, W. R., Granville, A., and Pomerance, C.. There are infinitely many Carmichael numbers. Annals Math. 140 (1994), 703–722.CrossRefGoogle Scholar
2.Davenport, H.. Multiplicative Number Theory (second edition, revised by H. L. Montgomery) (Springer-Verlag, New York, 1980).CrossRefGoogle Scholar
3.Gallagher, P. X.. A large sieve density estimate near σ= 1. Invent. Math. 16 (1970), 329–339.CrossRefGoogle Scholar
4.Halberstam, H., and Richert, H. E.. Sieve Methods. London Mathematical Society Monographs, No. 4, Academic Press (London, 1974).Google Scholar
5.Landau, E.. Über die imaginär-quadratischer Zahlkörper mit gleichen Klassenzahl. Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. II (1918), 277–284.Google Scholar
6.Landau, E.. Uber die Klassenzahl imaginär-quadratischer Zahlkörper. Göttingen Math.-Phys. Kl. 11 (1918), 285–295.Google Scholar
7.Page, A.. On the number of primes in an arithmetic progression. Proc. London Math. Soc. (2) 39 (1935), 116–141.CrossRefGoogle Scholar