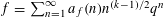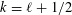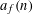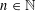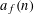Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kumari, Moni
and
Murty, M. Ram
2018.
Simultaneous non-vanishing and sign changes of Fourier coefficients of modular forms.
International Journal of Number Theory,
Vol. 14,
Issue. 08,
p.
2291.