Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T02:14:09.507Z Has data issue: false hasContentIssue false
  • English
  • Français

On the asymptotic properties of linear differential equations

Part of: Qualitative theory

Published online by Cambridge University Press:  26 February 2010

B. J. Harris
B. J. Harris
Affiliation:
Department of Mathematical Sciences, Northern Illinois University, De Kalb, Illinois 60115-2888, U.S.A.
Get access

Extract

We consider the second order linear differential equation

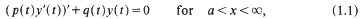
where p and q are real-valued members of 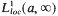with p(t)>0 for t ∈ [α, ∞). In particular we consider the following three questions dealing with the asymptotic behavior of solutions of (1.1).

MSC classification

Secondary: 34C10: Oscillation theory, zeros, disconjugacy and comparison theory
Type
Research Article
Information
Mathematika , Volume 34 , Issue 2 , December 1987 , pp. 187 - 198
Copyright
Copyright © University College London 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Atkinson, F. V.. On second order linear oscillations. Rev. Mat. Fis. Teor (Turcoman), Ser. A, 8 (1951), 71–87.Google Scholar
2.Atkinson, F. V.. Asymptotic formulae for linear oscillations. Proc. Glasgow Math. Assoc., 3 (1957), 105–111.Google Scholar
3.Cassell, J. S.. An extension of the Liouville Green asymptotic formula for oscillatory second order differential equations. Proc. Royal Soc. Edinburgh, 100 A (1985), 180–190.CrossRefGoogle Scholar
4.Cassel, J. S.. Generalized Liouville Green asymptotic approximation for second order differential equations. Proc. Royal Soc. Edinburgh, 103A (1986), 229–239.CrossRefGoogle Scholar
5.Hartman, P.. Ordinary differential equations (Wiley, New York, 1964).Google Scholar
6.Harris, B. J.. On the zeros of solutions of differential equations. J. London Math. Soc. (2), 27 (1983), 447–464.Google Scholar
7.Harris, B. J.. Limit circle criteria for second order differential expressions. Quart. J. Math. Oxford (2), 35 (1984), 415–427.CrossRefGoogle Scholar
8.Harris, B. J.. On the oscillation of solutions of linear differential equations. Mathematika, 31 (1984), 214–226.CrossRefGoogle Scholar