Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-28T06:47:20.218Z Has data issue: false hasContentIssue false
  • English
  • Français

On the construction of measures

Published online by Cambridge University Press:  26 February 2010

J. D. Knowles
J. D. Knowles
Affiliation:
Westfield College, London, N.W.3.
Get access

Extract

1. Given a metric space (X, ρ) a family 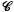of subsets of X which includes the empty set Ø, and a non-negative function τ on 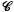with τ(Ø)=0, an outer measure μ* may be defined by

where empty infimums have value +∞. It is easily seen that μ* is a metric outer measure [i.e., if ρ(A, B)>0 then μ*(A∪B)=μ*(A)+μ*(B)] and from this it follows that all Borel sets in X are μ*-measurable.

Type
Research Article
Information
Mathematika , Volume 13 , Issue 1 , June 1966 , pp. 60 - 68
Copyright
Copyright © University College London 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Munroe, M., Measure and integration (Addison-Wesley, 1953).Google Scholar
2. Rogers, C. and Sion, M., “On Hausdorff measures in topologioal spaces”, Monatsh. Math. 67 (1963), 269–278.CrossRefGoogle Scholar
3. Sion, M. and Willmott, R., “Hausdorff measures in abstract spaces”, Trans. American Math. Soc. (to appear).Google Scholar
4. Bledsoe, W. and Morse, A. P., “A topological measure construction”, Pacific J. of Math. 13 (1963), 1067–1076.Google Scholar