Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T21:37:37.896Z Has data issue: false hasContentIssue false
  • English
  • Français

On the distribution of the roots of polynomial congruences

Published online by Cambridge University Press:  26 February 2010

C. Hooley
C. Hooley
Affiliation:
The Department of Mathematics, The University of Bristol
Get access

Extract

In a recent paper on a divisor problem the author showed incidentally that there is a certain regularity in the distribution of the roots of the congruence

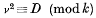
for variable k, where D is a fixed integer that is not a perfect square. In fact, to be more precise, it was shown that the ratios v/k, when arranged in the obvious way, are uniformly distributed in the sense of Weyl. In this paper we shall prove that a similar result is true when the special quadratic congruence above is replaced by the general polynomial congruence

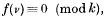
where f(u) is any irreducible primitive polynomial of degree greater than one. An entirely different procedure is adopted, since the method used in the former paper is only applicable to quadratic congruences.

Type
Research Article
Information
Mathematika , Volume 11 , Issue 1 , June 1964 , pp. 39 - 49
Copyright
Copyright © University College London 1964

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† “On the number of divisors of quadratic polynomials”, Acta Math., 110 (1963), 97–114.CrossRefGoogle Scholar

‡ For quadratic congruences, however, the method in † yields more precise results.

§ Proc. Inter. Congress. Math., 1962.

page43 note04 † See, for example, Nagell, T., Introduction to Number Theory, Chapter 3, Theorem 54. (Almqvist and Wiksell).Google Scholar

page43 note05 ‡ Erdős, P., “On the sum ∑d{f(k)}”, Journal London Math. Soc, 27 (1952), 7–15.Google Scholar

page43 note06 § Dedekind, R., Gesammelte Math. Werke, 1, 202–232.Google Scholar

page45 note07 † Hardy, G. H., and Ramanujan, S., “The normal number of prime factors of a number n”, Quart. J. Math., 48 (1917), 76–92.Google Scholar

page49 note08 † See Proc. London Math. Soc. (3), 7 (1957), 396–413.Google Scholar