Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-13T07:45:46.501Z Has data issue: false hasContentIssue false
  • English
  • Français

On the exponent of convergence of a packing of spheres

Published online by Cambridge University Press:  26 February 2010

D. G. Larman
D. G. Larman
Affiliation:
School of Mathematical and Physical Sciences, University of Sussex, Falmer, Brighton.
Get access

Extract

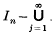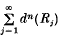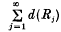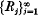Suppose, in n-dimensional Euclidean space, a sequence of disjoint closed spheres is packed into the open unit n-cube In in such a way as to ensure that the residual set has zero volume. Then, of course, is convergent and it can be shown, for n = 2, that is divergent. Let the exponent of convergence of the packing be the supremum of those real numbers t such that 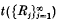is divergent and let tn denote inf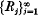, where the infimum is taken over all packings which satisfy the above conditions. In recent work Z. A. Melzak [1] has been interested in finding estimates for 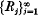in two-dimensional space. He has shown that t may take the value 2 and has produced some estimates for the Apollonius packing of disks. In this note we produce what is, perhaps, the most interesting estimate for tn by showing that tn is greater than n-1. Let sn denote the exact lower bound of the Besicovitch dimensions of every residual set which is formed by a packing of spheres in In.

Type
Research Article
Information
Mathematika , Volume 13 , Issue 1 , June 1966 , pp. 57 - 59
Copyright
Copyright © University College London 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Melzak, Z. A., to appear in Canadian. J. of Math.Google Scholar
2. Larman, D. G., “A note on the Besicovitch dimension of the closest packing of spheres in Rn”, to appear in Proc. Cambridge Phil. Soc.Google Scholar