Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Philpott, M R
1966.
The retarded interaction between electronically excited molecules.
Proceedings of the Physical Society,
Vol. 87,
Issue. 3,
p.
619.
Gomberoff, L.
McLone, R. R.
and
Power, E. A.
1966.
Long-Range Retarded Potentials between Molecules.
The Journal of Chemical Physics,
Vol. 44,
Issue. 11,
p.
4148.
Gomberoff, L
and
Power, E A
1966.
The resonance transfer of excitation.
Proceedings of the Physical Society,
Vol. 88,
Issue. 2,
p.
281.
1966.
Retardation in non-dispersive interactions between molecules.
Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences,
Vol. 295,
Issue. 1443,
p.
476.
1966.
Exciton-photon coupling in molecular crystals.
Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences,
Vol. 292,
Issue. 1428,
p.
78.
Avery, J S
1966.
Resonance energy transfer and spontaneous photon emission.
Proceedings of the Physical Society,
Vol. 88,
Issue. 1,
p.
1.
Meath, William J.
and
Hirschfelder, Joseph O.
1966.
Long-Range (Retarded) Intermolecular Forces.
The Journal of Chemical Physics,
Vol. 44,
Issue. 9,
p.
3210.
Avery, J S
1966.
The retarded dipole-dipole interaction in exciton theory.
Proceedings of the Physical Society,
Vol. 89,
Issue. 3,
p.
677.
Philpott, M R
1966.
Radiation damping of degenerate states: I. Theory and application to two-atom systems.
Proceedings of the Physical Society,
Vol. 89,
Issue. 2,
p.
217.
Power, Edwin A.
Meath, William J.
and
Hirschfelder, Joseph O.
1966.
Spin-Spin Interaction for Very Large Atomic Separations.
Physical Review Letters,
Vol. 17,
Issue. 15,
p.
799.
Philpott, M R
1967.
Radiation damping of degenerate states II. Two-photon transitions in two-molecule systems.
Proceedings of the Physical Society,
Vol. 90,
Issue. 1,
p.
143.
Power, Edwin A.
1967.
Advances in Chemical Physics.
Vol. 12,
Issue. ,
p.
167.
Hirschfelder, Joseph O.
and
Meath, William J.
1967.
Advances in Chemical Physics.
Vol. 12,
Issue. ,
p.
3.
Philpott, M R
1967.
Radiation damping of degenerate states: III. Fourth-order resonance interaction.
Proceedings of the Physical Society,
Vol. 91,
Issue. 3,
p.
520.
Philpott, M R
1968.
On exciton-photon coupling and retarded interactions in molecular crystals.
Journal of Physics C: Solid State Physics,
Vol. 1,
Issue. 1,
p.
42.
Meath, William J.
1968.
Retarded Interaction Energies between Like Atoms in Different Energy States.
The Journal of Chemical Physics,
Vol. 48,
Issue. 1,
p.
227.
Gomberoff, L.
1968.
Relativistic related operators and retarded multipole energies at resonance.
Il Nuovo Cimento A,
Vol. 56,
Issue. 1,
p.
97.
1969.
Retarded interactions in mixed crystal spectra.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 310,
Issue. 1502,
p.
297.
1969.
Theory of Intermolecular Forces.
p.
356.
1969.
Long range cut-off in the retarded two-molecule interaction.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 310,
Issue. 1502,
p.
313.
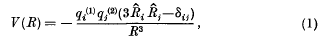
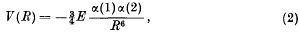
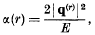
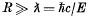 was given by Casimir and Polder as
was given by Casimir and Polder as