Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pomerance, Carl
1980.
Popular values of Euler's function.
Mathematika,
Vol. 27,
Issue. 1,
p.
84.
Guy, Richard K.
1981.
Unsolved Problems in Number Theory.
p.
25.
Fouvry, �tienne
1985.
Th�or�me de Brun-Titchmarsh; application au th�or�me de Fermat.
Inventiones Mathematicae,
Vol. 79,
Issue. 2,
p.
383.
Baker, R. C.
and
Harman, G.
1996.
Analytic Number Theory.
p.
39.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
71.
Banks, William D.
and
Shparlinski, Igor E.
2007.
On values taken by the largest prime factor of shifted primes.
Journal of the Australian Mathematical Society,
Vol. 82,
Issue. 1,
p.
133.
Baker, Roger
2009.
Numbers in a given set with (or without) a large prime factor.
The Ramanujan Journal,
Vol. 20,
Issue. 3,
p.
275.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
369.
Wu, Jie
and
Xi, Ping
2021.
Arithmetic exponent pairs for algebraic trace functions and applications.
Algebra & Number Theory,
Vol. 15,
Issue. 9,
p.
2123.
Sanna, Carlo
2022.
A survey on coefficients of cyclotomic polynomials.
Expositiones Mathematicae,
Vol. 40,
Issue. 3,
p.
469.
Jiang, Yujiao
Lü, Guangshi
and
Wang, Zhiwei
2022.
Averaged forms of two conjectures of Erdős and Pomerance, and their applications.
Advances in Mathematics,
Vol. 409,
Issue. ,
p.
108592.
DING, YUCHEN
2025.
ON A CONJECTURE ON SHIFTED PRIMES WITH LARGE PRIME FACTORS, II.
Bulletin of the Australian Mathematical Society,
Vol. 111,
Issue. 1,
p.
48.

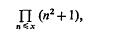
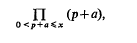
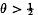 such that
such that 