Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Anderson, Robert J.
1980.
On the Mertens conjecture for cusp forms,
Corrigendum
.
Mathematika,
Vol. 27,
Issue. 2,
p.
261.
Anderson, Robert J.
and
Stark, H. M.
1981.
Analytic Number Theory.
Vol. 899,
Issue. ,
p.
79.
Grupp, F.
1982.
On the Mertens conjecture for cusp forms.
Mathematika,
Vol. 29,
Issue. 2,
p.
213.
Terras, Audrey
2013.
Harmonic Analysis on Symmetric Spaces—Euclidean Space, the Sphere, and the Poincaré Upper Half-Plane.
p.
1.
Terras, Audrey
2013.
Harmonic Analysis on Symmetric Spaces—Euclidean Space, the Sphere, and the Poincaré Upper Half-Plane.
p.
149.
Terras, Audrey
2013.
Harmonic Analysis on Symmetric Spaces—Euclidean Space, the Sphere, and the Poincaré Upper Half-Plane.
p.
107.
Jiang, Yujiao
and
Lü, Guangshi
2019.
On automorphic analogues of the Möbius randomness principle.
Journal of Number Theory,
Vol. 197,
Issue. ,
p.
268.
HU, DANIEL
KANEKO, IKUYA
MARTIN, SPENCER
and
SCHILDKRAUT, CARL
2024.
On a Mertens-type conjecture for number fields.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 177,
Issue. 3,
p.
481.

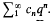 We shall assume that
We shall assume that 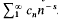 The series and the product
The series and the product