Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T17:55:47.412Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE METRIC ENTROPY OF THE BANACH–MAZUR COMPACTUM

Part of: Normed linear spaces and Banach spaces; Banach lattices Selfadjoint operator algebras

Published online by Cambridge University Press:  28 May 2014

Gilles Pisier
Gilles Pisier*
Affiliation:
Texas A&M University, College Station, TX 77843, U.S.A. email pisier@math.tamu.edu Université Paris VI, Inst. Math. Jussieu, Équipe d’Analyse Fonctionnelle, Case 186, 75252 Paris Cedex 05, France
Get access

Abstract

We study the metric entropy of the metric space 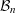${\mathcal{B}}_{n}$ of all $n$-dimensional Banach spaces (the so-called Banach–Mazur compactum) equipped with the Banach–Mazur (multiplicative) “distance” 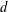$d$. We are interested either in estimates independent of the dimension or in asymptotic estimates when the dimension tends to 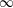$\infty$. For instance, we prove that, if 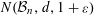$N({\mathcal{B}}_{n},d,1+{\it\varepsilon})$ is the smallest number of “balls” of “radius” 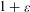$1+{\it\varepsilon}$ that cover 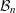${\mathcal{B}}_{n}$, then for any 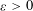${\it\varepsilon}>0$ we have

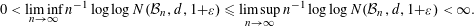$$\begin{eqnarray}0<\liminf _{n\rightarrow \infty }n^{-1}\log \log N({\mathcal{B}}_{n},d,1+{\it\varepsilon})\leqslant \limsup _{n\rightarrow \infty }n^{-1}\log \log N({\mathcal{B}}_{n},d,1+{\it\varepsilon})<\infty .\end{eqnarray}$$
We also prove an analogous result for the metric entropy of the set of $n$-dimensional operator spaces equipped with the distance 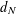$d_{N}$ naturally associated with 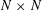$N\times N$ matrices with operator entries. In that case 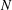$N$ is arbitrary but our estimates are valid independently of 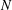$N$. In the Banach space case (i.e. 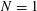$N=1$) the above upper bound is part of the folklore, and the lower bound is at least partially known (but apparently has not appeared in print). 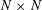While we follow the same approach in both cases, the matricial case requires more delicate ingredients, namely estimates (from our previous work) on certain $n$-tuples of $N\times N$ unitary matrices known as “quantum expanders”.

MSC classification

Primary: 46B07: Local theory of Banach spaces 46L07: Operator spaces and completely bounded maps
Type
Research Article
Information
Mathematika , Volume 61 , Issue 1 , January 2015 , pp. 179 - 198
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barvinok, A., Thrifty approximations of convex bodies by polytopes. Int. Math. Res. Not. 2013, doi:10.1093/imrn/rnt078.Google Scholar
Barvinok, A. and Alexander, E. Veomett, The computational complexity of convex bodies. In Surveys on Discrete and Computational Geometry (Contemporary Mathematics 453), American Mathematical Society (Providence, RI, 2008), 117–137.Google Scholar
Bourgain, J., Lindenstraus, J. and Milman, V., Aproximation of zonoids by zonotopes. Acta Math. 162 1989, 73–141.CrossRefGoogle Scholar
Bronstein, E.M., 𝜀-entropy of affine-equivalent convex bodies and Minkowski’s compactum. Optimizatsiya 22(39) 1978, 5–11 ; 155 (Russian).Google Scholar
Bronstein, E.M., Approximation of convex sets by polytopes. J. Math. Sci. 153 2008, 727–762.Google Scholar
Conway, J. H. and Sloane, N. J. A., Sphere Packings, Lattices and Groups, 3rd edition, Springer (New York, 1999).CrossRefGoogle Scholar
Effros, E.G. and Ruan, Z.J., Operator Spaces, The Clarendon Press, Oxford University Press (New York, 2000).Google Scholar
Elton, J., Sign-embeddings of ℓ 1n. Trans. Amer. Math. Soc. 279 1983, 113–124.Google Scholar
Gluskin, E. D., The diameter of the Minkowski compactum is roughly equal to n. Funct. Anal. Appl. 15 1981, 72–73.Google Scholar
Gluskin, E. D., Probability in the Geometry of Banach spaces. In Proc. ICM, Vol. 2 (Berkeley, CA, 1986), 924–938 (Russian). Engl. transl. Amer. Math. Soc. Transl. Ser. 2 147 (1990) 35–49.Google Scholar
Haagerup, U. and Thorbjørnsen, S., Random matrices and K-theory for exact C ∗-algebras. Doc. Math. 4 1999, 341–450 (electronic).Google Scholar
Hastings, M., Random unitaries give quantum expanders. Phys. Rev. A (3) 76(3) 2007,032315.Google Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis. Vol. II: Structure and Analysis for Compact Groups. Analysis on Locally Compact Abelian Groups, Springer (New York–Berlin, 1970).Google Scholar
Junge, M. and Pisier, G., Bilinear forms on exact operator spaces and B (H) ⊗ B (H). Geom. Funct. Anal. 5(2) 1995, 329–363.Google Scholar
Litvak, A., Rudelson, M. and Tomczak-Jaegermann, N., On approximations by projections of polytopes with few facets. Israel J. Math. (to appear).Google Scholar
Marcus, M.B. and Pisier, G., Random Fourier Series with Applications to Harmonic Analysis (Annals of Mathematics Studies 101), Princeton University Press (Princeton, NJ, 1981).Google Scholar
Milman, V., Almost Euclidean quotient spaces of subspaces of a finite-dimensional normed space. Proc. Amer. Math. Soc. 94 1985, 445–449.Google Scholar
Pajor, A., Sous-Espaces ℓ 1n des Espaces de Banach, Travaux en cours. Herman (Paris, 1986).Google Scholar
Pisier, G., Remarques sur un résultat non publié de B. Maurey. Séminaire d’Analyse Fonctionnelle, 1980–1981, Exp. No. V, École Polytechnique, Palaiseau 1981, 13 pp. (available online at http://www.numdam.org/numdam-bin/feuilleter?id=SAF_1980-1981___).Google Scholar
Pisier, G., The Volume of Convex Bodies and Banach Space Geometry, Cambridge University Press (Cambridge, 1989).Google Scholar
Pisier, G., Introduction to Operator Space Theory, Cambridge University Press (Cambridge, 2003).Google Scholar
Pisier, G., Quantum Expanders and Geometry of Operator Spaces. J. Eur. Math. Soc. (to appear).Google Scholar
Schechtman, G., Embedding X pm Spaces into ℓ rn (Lecture Notes in Mathematics 1267), Springer (Berlin, 1987) 53–74.Google Scholar
Schechtman, G., More on embedding subspaces of L pin ℓ rn. Compositio Math. 61(2) 1987, 159–169.Google Scholar
Szarek, S., On the existence and uniqueness of complex structure and spaces with few operators. Trans. Amer. Math. Soc. 293 1986, 339–353.Google Scholar
Szarek, S., The finite-dimensional basis problem with an appendix on nets of Grassmann manifolds. Acta Math. 151 1983, 153–179.Google Scholar
Szarek, S., On the geometry of the Banach–Mazur compactum (Lecture Notes in Mathematics 1470), Springer (Berlin, 1991), 48–59.Google Scholar
Szarek, S., Convexity, complexity, and high dimensions. In Proc. Int. Cong. of Mathematicians (Madrid, August 22–30, 2006, Vol. II), European Mathematical Society (Zurich, Switzerland, 2006), 1599–1622.Google Scholar
Szarek, S., Isomorphic embeddings into $\ell _{\infty }^{N}$ and rough nets of the Banach–Mazur compactum, Private communication, Sept. 2013.Google Scholar
Szarek, S. and Tomczak-Jaegermann, N., Saturating constructions for normed spaces. Geom. Funct. Anal. 14 2004, 1352–1375.Google Scholar
Szarek, S. and Tomczak-Jaegermann, N., Saturating constructions for normed spaces. II. J. Funct. Anal. 221(2) 2005, 407–438.Google Scholar
Talagrand, M., Embedding subspaces of L 1into ℓ 1n. Proc. Amer. Math. Soc. 108(2) 1990, 363–369.Google Scholar
Tomczak-Jaegermann, N., Banach–Mazur Distances and Finite-Dimensional Operator Ideals, Longman, Wiley (New York, 1989).Google Scholar