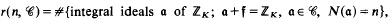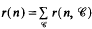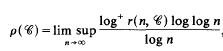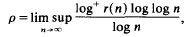Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
KANE, DANIEL M.
2013.
AN ASYMPTOTIC FOR THE NUMBER OF SOLUTIONS TO LINEAR EQUATIONS IN PRIME NUMBERS FROM SPECIFIED CHEBOTAREV CLASSES.
International Journal of Number Theory,
Vol. 09,
Issue. 04,
p.
1073.
Kim, Henry H.
2019.
Monogenic dihedral quartic extensions.
The Ramanujan Journal,
Vol. 50,
Issue. 2,
p.
459.