Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T17:36:38.405Z Has data issue: false hasContentIssue false
  • English
  • Français

On the representation of an integer as the sum of a large and a small square

Part of: Forms and linear algebraic groups

Published online by Cambridge University Press:  26 February 2010

R. R. Hall
R. R. Hall
Affiliation:
Department of Mathematics, University of York. Heslington, York YO10 5DD, U.K.
Get access

Extract

We continue our study of the different representations of an integer n as a sum of two squares initiated in our final paper written with Paul Erdős [1]. We let r(n) denote the number of representations n = a2 + b2 counted in the usual way, that is, with regard to both the order and sign of a and b. We have

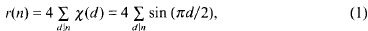
where x is the non-principal Dirichlet character (mod 4); moreover, r(n)≥0 if and only if n has no prime factor p ≡ 3 (mod 4) with odd exponent. We define the function b(n) on the sequence of representable numbers as the least possible value of |b|—for example, we have b(13) = 2,b(25) = 0, b(65) = 1—and we write

here and throughout the paper the star denotes that the sum is restricted to the representable integers. The problem considered here is to find an asymptotic formula for this sum, or, less ambitiously, to determine the order of magnitude of the function B(x).

MSC classification

Secondary: 11E25: Sums of squares and representations by other particular quadratic forms
Type
Research Article
Information
Mathematika , Volume 49 , Issue 1-2 , June 2002 , pp. 245 - 251
Copyright
Copyright © University College London 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Erdős, P. and Hall, R. R.. On the angular distribution of Gaussian integers with fixed norm. Discrete Math., 200 (1999), 87–94.CrossRefGoogle Scholar
2.Hall, R. R.. Sets of Multiples. Cambridge Tracts in Mathematics, 118 (1996).Google Scholar
3.Hardy, G. H. and Ramanujan, S.. The normal number of prime factors of a number n. Quart. J. Math., 48 (1917).Google Scholar
4.Hildebrand, A. and Tenenbaum, G., On the number of prime factors of an integer, Duke Math. J. 56 (1988).CrossRefGoogle Scholar
5.Kubilius, J.. The distribution of Gaussian primes in sectors and contours (in Russian). Leningrad Gos. Univ. Uc. Zap. 137, Ser. Mat. Nauk, 19 (1950) 40–52.Google Scholar
6.Selberg, A., Note on a paper by L. G. Sathe, J. Indian Math. Soc. 18 (1954) 83–87.Google Scholar
7.Tenenbaum, G., Introduction à la Théorie Analytique et Probabiliste des Nombres. Institute Elie Cartan, Tome 13, Nancy (1990).Google Scholar