Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T14:43:09.336Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE SPECTRUM OF DIOPHANTINE APPROXIMATION CONSTANTS

Part of: Geometry of numbers Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  22 June 2015

Johannes Schleischitz
Johannes Schleischitz*
Affiliation:
Institute of Mathematics, University of Natural Resources and Life Sciences, Vienna, Austria email johannes.schleischitz@boku.ac.at
Get access

Abstract

The approximation constant 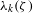${\it\lambda}_{k}({\it\zeta})$ is defined as the supremum of 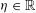${\it\eta}\in \mathbb{R}$ such that the estimate 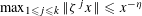$\max _{1\leqslant j\leqslant k}\Vert {\it\zeta}^{j}x\Vert \leqslant x^{-{\it\eta}}$ has infinitely many integer solutions $x$. Here $\Vert .\Vert$ denotes the distance to the closest integer. We establish a connection on the joint spectrum 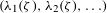$({\it\lambda}_{1}({\it\zeta}),{\it\lambda}_{2}({\it\zeta}),\ldots )$, which will lead to various improvements of known results on the individual spectrum of the approximation constants 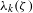${\it\lambda}_{k}({\it\zeta})$ as well. In particular, for given 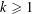$k\geqslant 1$ and 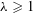${\it\lambda}\geqslant 1$, we construct 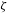${\it\zeta}$ in the Cantor set with 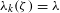${\it\lambda}_{k}({\it\zeta})={\it\lambda}$. Moreover, we establish an estimate for the uniform approximation constants 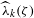$\widehat{{\it\lambda}}_{k}({\it\zeta})$, which enables us to determine classical approximation constants for Liouville numbers.

MSC classification

Primary: 11H06: Lattices and convex bodies
Secondary: 11J13: Simultaneous homogeneous approximation, linear forms 11J25: Diophantine inequalities 11J82: Measures of irrationality and of transcendence 11J83: Metric theory
Type
Research Article
Information
Mathematika , Volume 62 , Issue 1 , 2016 , pp. 79 - 100
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beresnevich, V., Rational points near manifolds and metric Diophantine approximation. Ann. of Math. (2) 175(1) 2012, 187–235.CrossRefGoogle Scholar
Beresnevich, V., Dickinson, D. and Velani, S. L., Diophantine approximation on planar curves and the distribution of rational points. Ann. of Math. (2) 166 2007, 367–426 with an appendix by R. C. Vaughan: Sums of two squares near perfect squares.CrossRefGoogle Scholar
Budarina, N., Dickinson, D. and Levesley, J., Simultaneous Diophantine approximation on polynomial curves. Mathematika 56 2010, 77–85.CrossRefGoogle Scholar
Bugeaud, Y., Approximation by Algebraic Numbers (Cambridge Tracts in Mathematics) (Cambridge, 2004).CrossRefGoogle Scholar
Bugeaud, Y., Diophantine approximation and Cantor sets. Math. Ann. 341 2008, 677–684.CrossRefGoogle Scholar
Bugeaud, Y., On simultaneous rational approximation to a real number and its integral powers. Ann. Inst. Fourier (Grenoble) 60(6) 2010, 2165–2182.CrossRefGoogle Scholar
Bugeaud, Y. and Laurent, M., Exponents in Diophantine approximation. In Diophantine Geometry Proceedings, Scuola Normale Superiore Pisa (Ser. CRM 4) (2007), 101–121.Google Scholar
Davenport, H. and Schmidt, W. M., Approximation to real numbers by algebraic integers. Acta Arith. 15 1969, 393–416.CrossRefGoogle Scholar
German, O., On Diophantine exponents and Khintchine’s transference principle. Mosc. J. Comb. Number Theory 2 2012, 22–51.Google Scholar
Jarník, V., Über die simultanen Diophantische Approximationen. Math. Z. 33 1931, 505–543.CrossRefGoogle Scholar
Khintchine, A. Y., Über eine Klasse linearer diophantischer Approximationen. Rend. Circ. Mat. Palermo (2) 50 1926, 706–714.CrossRefGoogle Scholar
Laurent, M., On simultaneous rational approximation to successive powers of a real number. Indag. Math. (N.S.) 14(1) 2003, 45–53.CrossRefGoogle Scholar
Levesley, J., Salp, C. and Velani, V., On a problem of K. Mahler: Diophantine approximation and Cantor sets. Math. Ann. 388(1) 2007, 97–118.CrossRefGoogle Scholar
Mendès France, M., Sur les fractions continues limitées. Acta Arith. 23 1973, 207–215.CrossRefGoogle Scholar
Minkowski, H., Geometrie der Zahlen, Teubner (Leipzig, 1910).Google Scholar
Perron, O., Lehre von den Kettenbrüchen, Teubner (Leipzig, 1913).Google Scholar
Roth, K. F., Rational approximations to algebraic numbers. Mathematika 2 1955, 1–20.CrossRefGoogle Scholar
Roy, D., Approximation simultannée d’un nombre et de son carré. C. R. Math. Acad. Sci. Paris 336 2003, 1–6.CrossRefGoogle Scholar
Roy, D., Approximation to real numbers by cubic algebraic integers I. Proc. Lond. Math. Soc. (3) 88 2004, 42–62.CrossRefGoogle Scholar
Roy, D., Diophantine approximation in small degree. In Number Theory: Proceedings from the 7th Conference of the Canadian Number Theory Association (CRM Proceedings & Lecture Notes 36), American Mathematical Society (Providence, RI, 2004), 269–285.CrossRefGoogle Scholar
Roy, D., On simultaneous rational approximations to a real number, its square and its cube. Acta Arith. 133 2008, 185–197.CrossRefGoogle Scholar
Schmidt, W., Norm form equations. Ann. of Math. (2) 96 1972, 526–551.CrossRefGoogle Scholar
Sprindžuk, V. G., A proof of Mahler’s conjecture on the measure of the set of S-numbers. Izv. Akad. Nauk SSSR Ser. Mat. 29 1965, 379–436; translation in Amer. Math. Soc. Transl. 51 (1966), 215–272.Google Scholar
Vaughan, R. C. and Velani, S., Diophantine approximation on planar curves: the convergence theory. Invent. Math. 166 2006, 103–124.CrossRefGoogle Scholar