Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jacobson, Marcel
and
Jarden, Moshe
1985.
On torsion of abelian varieties over large algebraic extensions of finitely generated fields:
Erratum
.
Mathematika,
Vol. 32,
Issue. 2,
p.
316.
Fried, Michael D.
and
Jarden, Moshe
1986.
Field Arithmetic.
p.
248.
Geyer, Wulf-Dieter
and
Jarden, Moshe
2005.
Torsion of abelian varieties over large algebraic fields.
Finite Fields and Their Applications,
Vol. 11,
Issue. 1,
p.
123.
JARDEN, MOSHE
and
PETERSEN, SEBASTIAN
2019.
TORSION OF ABELIAN VARIETIES OVER LARGE ALGEBRAIC EXTENSIONS OF.
Nagoya Mathematical Journal,
Vol. 234,
Issue. ,
p.
46.
Asayama, Takuya
2021.
Torsion points of Drinfeld modules over large algebraic extensions of finitely generated function fields.
Journal of Number Theory,
Vol. 226,
Issue. ,
p.
358.
Asayama, Takuya
and
Taguchi, Yuichiro
2025.
Mordell–Weil groups over large algebraic extensions of fields of characteristic zero.
Research in Number Theory,
Vol. 11,
Issue. 4,

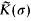 the following results hold.
the following results hold.