No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 26 February 2010
It was proved recently by Roth that if α is any real algebraic number, and κ > 2, then the inequality
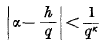
has only a finite number of solutions in integers h and q, where q > 0 and (h, q) = 1. This remarkable result answered finally a question which had been only partially answered by the work of Thue and Siegel.
page 40 note † Mathematika, 2 (1955), 1–20. This paper will be referred to as R.CrossRefGoogle Scholar
page 40 note ‡ Math. Annalen, 107 (1933), 691–730.CrossRefGoogle Scholar
page 40 note § See, for example, Waerden, van der, Moderne Algebra I (New York, 1953), 235–243.Google Scholar
page 41 note † Loc. cit., Hilfsatz 5 and §18.
page 41 note ‡ Math. Annalen, 108 (1933), 37–55.
page 47 note ‡ Mahler, lco. cit., 701.