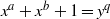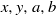Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hajdu, Lajos
and
Pink, István
2014.
On the Diophantine equation 1+2a+xb=yn.
Journal of Number Theory,
Vol. 143,
Issue. ,
p.
1.
Laishram, Shanta
and
Luca, Florian
2014.
Fibonacci Numbers of the Form
x
a
±
x
b
± 1
.
The Fibonacci Quarterly,
Vol. 52,
Issue. 4,
p.
290.
Bennett, Michael A.
and
Scheerer, Adrian-Maria
2017.
Number Theory – Diophantine Problems, Uniform Distribution and Applications.
p.
83.
Ghioca, Dragos
Ostafe, Alina
Saleh, Sina
and
Shparlinski, Igor E.
2022.
On sparsity of representations of polynomials as linear combinations of exponential functions.
Journal of the London Mathematical Society,
Vol. 105,
Issue. 4,
p.
2076.
Kaneko, Hajime
and
Stoll, Thomas
2022.
Products of Integers with Few Nonzero Digits.
Uniform distribution theory,
Vol. 17,
Issue. 1,
p.
11.
Aloui, Karam
Jamet, Damien
Kaneko, Hajime
Kopecki, Steffen
Popoli, Pierre
and
Stoll, Thomas
2023.
On the binary digits of n and n2.
Theoretical Computer Science,
Vol. 939,
Issue. ,
p.
119.
Fei, Shuanglin
Zhu, Guangyan
and
Wu, Rongjun
2024.
On a conjecture concerning the exponential Diophantine equation $ (an^{2}+1)^{x}+(bn^{2}-1)^{y} = (cn)^{z} $.
Electronic Research Archive,
Vol. 32,
Issue. 6,
p.
4096.
Bérczes, Attila
Pethő, Attila
and
Pink, István
2025.
Perfect powers with few digits in a canonical number system.
Mathematika,
Vol. 71,
Issue. 4,