Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T22:09:56.907Z Has data issue: false hasContentIssue false
  • English
  • Français

THE POWER-SAVING MANIN–PEYRE CONJECTURE FOR A SENARY CUBIC

Part of: Zeta and $L$-functions: analytic theory Diophantine equations Multiplicative number theory

Published online by Cambridge University Press:  22 May 2019

Sandro Bettin  and
Kevin Destagnol
Sandro Bettin
Affiliation:
DIMA – Dipartimento di Matematica, Via Dodecaneso 35, 16146 Genova, Italy email bettin@dima.unige.it
Kevin Destagnol
Affiliation:
Max Planck Institut für Mathematik, Vivatsgasse 7, 53111 Bonn, Germany email kdestagnol@mpim-bonn.mpg.de
Get access

Abstract

Using work of the first author [S. Bettin, High moments of the Estermann function. Algebra Number Theory 47(3) (2018), 659–684], we prove a strong version of the Manin–Peyre conjectures with a full asymptotic and a power-saving error term for the two varieties respectively in $\mathbb{P}^{2}\times \mathbb{P}^{2}$ with bihomogeneous coordinates 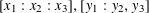$[x_{1}:x_{2}:x_{3}],[y_{1}:y_{2},y_{3}]$ and in $\mathbb{P}^{1}\times \mathbb{P}^{1}\times \mathbb{P}^{1}$ with multihomogeneous coordinates 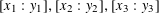$[x_{1}:y_{1}],[x_{2}:y_{2}],[x_{3}:y_{3}]$ defined by the same equation 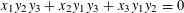$x_{1}y_{2}y_{3}+x_{2}y_{1}y_{3}+x_{3}y_{1}y_{2}=0$. We thus improve on recent work of Blomer et al [The Manin–Peyre conjecture for a certain biprojective cubic threefold. Math. Ann. 370 (2018), 491–553] and provide a different proof based on a descent on the universal torsor of the conjectures in the case of a del Pezzo surface of degree 6 with singularity type 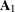$\mathbf{A}_{1}$ and three lines (the other existing proof relying on harmonic analysis by Chambert-Loir and Tschinkel [On the distribution of points of bounded height on equivariant compactifications of vector groups. Invent. Math. 148 (2002), 421–452]). Together with Blomer et al [On a certain senary cubic form. Proc. Lond. Math. Soc. 108 (2014), 911–964] or with work of the second author [K. Destagnol, La conjecture de Manin pour une famille de variétés en dimension supérieure. Math. Proc. Cambridge Philos. Soc. 166(3) (2019), 433–486], this settles the study of the Manin–Peyre conjectures for this equation.

MSC classification

Primary: 11D45: Counting solutions of Diophantine equations 11N37: Asymptotic results on arithmetic functions 11M41: Other Dirichlet series and zeta functions
Type
Research Article
Information
Mathematika , Volume 65 , Issue 4 , 2019 , pp. 789 - 830
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batyrev, V. V. and Tschinkel, Y., Manin’s conjecture for toric varieties. Algebr. Geom. 7(1) 1998, 15–53.Google Scholar
Batyrev, V. V. and Tschinkel, Y., Tamagawa numbers of polarized algebraic varieties. Astérisque 251 1998, 79–89.Google Scholar
Bettin, S., High moments of the Estermann function. Algebra Number Theory 47(3) 2018, 659–684.Google Scholar
Bettin, S., Linear correlations of the divisor function. Acta Arith. 188 2019, 1–52.10.4064/aa170228-21-6Google Scholar
Birch, B. J., Forms in many variables. Proc. R. Soc. Lond. Ser. A 265 1962, 245–263.Google Scholar
Blomer, V. and Brüdern, J., The density of rational points on a certain threefold. In Contributions to Analytic and Algebraic Number Theory (Springer Proceedings in Mathematics 9 ) (eds Blomer, V. and Mihailescu, P.), Springer (New York, 2012), 1–15.10.1007/978-1-4614-1219-9Google Scholar
Blomer, V., Brüdern, J. and Salberger, P., On a certain senary cubic form. Proc. Lond. Math. Soc. 108 2014, 911–964.10.1112/plms/pdt043Google Scholar
Blomer, V., Brüdern, J. and Salberger, P., The Manin–Peyre conjecture for a certain biprojective cubic threefold. Math. Ann. 370 2018, 491–553.10.1007/s00208-017-1621-4Google Scholar
de la Bretèche, R., Estimation de sommes multiples de fonctions arithmétiques. Compos. Math. 128(3) 2001, 261–298.10.1023/A:1011803816545Google Scholar
de la Bretèche, R., Nombre de points rationnels sur la cubique de Segre. Proc. Lond. Math. Soc. 95(1) 2007, 69–155.10.1112/plms/pdm001Google Scholar
de la Bretèche, R., Sur le nombre de matrices aléatoires à coefficients rationnels. Q. J. Math. 68(3) 2017, 935–955.10.1093/qmath/hax006Google Scholar
de la Bretèche, R. and Browning, T., On Manin’s conjecture for singular del Pezzo surfaces of degree four, I. Michigan Math. J. 55 2007, 51–80.10.1307/mmj/1177681985Google Scholar
de la Bretèche, R., Browning, T. and Peyre, E., On Manin’s conjecture for a family of Châtelet surfaces. Ann. of Math. (2) 175 2012, 297–343. A longer version is also available at arXiv:1002.0255.10.4007/annals.2012.175.1.8Google Scholar
de la Bretèche, R. and Tenenbaum, G., Sur les processus arithmétiques liés aux diviseurs. Adv. Appl. Probab. 48A (volume en l’honneur de Bingham) (2016).Google Scholar
Browning, T. D., Quantitative Arithmetic of Projective Varieties, Birkhäuser (2009).10.1007/978-3-0346-0129-0Google Scholar
Browning, T. D. and Derenthal, U., Manin’s conjecture for a quartic del Pezzo surface with A 4 singularity. Ann. Inst. Fourier (Grenoble) 59(3) 2009, 1231–1265.10.5802/aif.2462Google Scholar
Browning, T. D. and Heath-Brown, D. R., Forms in many variables and differing degrees. J. Eur. Math. Soc. (JEMS) 9 2017, 357–394.10.4171/JEMS/668Google Scholar
Chambert-Loir, A. and Tschinkel, Y., On the distribution of points of bounded height on equivariant compactifications of vector groups. Invent. Math. 148 2002, 421–452.10.1007/s002220100200Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., La descente sur les variétés rationnelles, II. Duke Math. J. 54 1987, 375–492.10.1215/S0012-7094-87-05420-2Google Scholar
Derenthal, U., Geometry of universal torsors. PhD Thesis, Georg-August-Universität zu Göttingen, 2006.Google Scholar
Destagnol, K., La conjecture de Manin pour une famille de variétés en dimension supérieure. Math. Proc. Cambridge Philos. Soc. 166(3) 2019, 433–486.10.1017/S030500411800004XGoogle Scholar
Franke, J., Manin, Y. and Tschinkel, Y., Rational points of bounded height on Fano varieties. Invent. Math. 54 1987, 375–492.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Tables of Integrals, Series, and Products, 7th edn., Elsevier/Academic Press (Amsterdam, 2007). Translated from the Russian, translation edited and with a preface by Alan Jeffrey and Daniel Zwillinger.Google Scholar
Hall, R. R., Sets of Multiples (Cambridge Tracts in Mathematics 118 ), Cambridge University Press (Cambridge, 1996).10.1017/CBO9780511566011Google Scholar
Loughran, D., Manin’s conjecture for a singular sextic del Pezzo surface. J. Théor. Nombres Bordeaux 22(3) 2010, 675–701.10.5802/jtnb.739Google Scholar
Peyre, E., Hauteurs et mesures de Tamagawa sur les variétés de Fano. Duke Math. J. 79 1995, 101–218.10.1215/S0012-7094-95-07904-6Google Scholar
Peyre, E., Points de hauteur bornée, topologie adélique et mesures de Tamagawa. J. Théor. Nombres Bordeaux 15 2003, 319–349. Les XXIIèmes Journées Arithmétiques (Lille, 2001).10.5802/jtnb.405Google Scholar
Salberger, P., Tamagawa numbers of universal torsors and points of bounded height on Fano varieties. Astérisque 251 1998, 91–258.Google Scholar
Schmidt, W., Northcott’s theorem on heights. II. The quadratic case. Acta Arith. 70 1995, 343–375.10.4064/aa-70-4-343-375Google Scholar
Tanimoto, S. and Tschinkel, Y., Height zeta functions of equivariant compactifications of semi-direct products of algebraic groups. Contemp. Math. 566 2012, 119–157.10.1090/conm/566/11218Google Scholar
Titchmarsh, E. C., Introduction to the Theory of Fourier Integrals, 3rd edn., Chelsea (New York, 1986).Google Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-Function, 2nd edn., Oxford University Press (New York, 1986). Edited and with a preface by D. R. Heath-Brown.Google Scholar